【题解】F-Variety Split Hard

F-Variety Split Hard

题意

给定一个长度为 \(n\) 的序列 \(a\)，你可以把其划分成 \(3\) 个非空部分，三部分应连续，使这三部分不同的数的个数和最大，输出这个最大值 \(s\)。

思路

首先感觉这个非空的限制没有什么用，因为我们要使不同的数的个数和最大，应该尽量使他们划分为不同的两部分，而为了使其处于不同的两部分，我们的划分不可能非空。

我们注意到 \(s\) 一定不小于 \(a\) 中数的种类数，之后我们考虑怎样划分才能使 \(s\) 尽可能大，我们画一下图，\(x,y,z \ne 1\)：

只有分界线是红线时两个 \(1\) 才会产生贡献。

我们很自然想到可以用 线段树 来维护，我们把上图两个 \(1\) 产生的额外贡献计为一个 \(1\)，我们维护用线将 \(a_i\) 与 \(a_{i+1}\) 分离开的额外贡献，计为 \(f_i\)，\(i \le n-1\)。

那么，对于两个相同且这两个数相对相邻，如上图的两个 \(1\)，我们就可以从第一个 \(1\) 的位置开始，到第二个 \(1\) 的位置减一结束，因为把分界线放至第二个 \(1\) 后无法产生额外贡献。

这样找最大值我们就得到的 ABC397C 的一种唐诗解法。

我们考虑要划两条线，所以我们要考虑如果我们把线放到位置 \(i\) 上，有哪些位置上的额外贡献回减，也就是在 \(i\) 的左边的和在 \(i\) 右边的相同的数，且在之前加过这个区间的两数，如果我把第二条线放到这两数形成的左闭右开区间内，那么我们应该要把这个额外贡献减去，体现在线段树上就是区间减。

但我们需要每一个 \(i\) 都要这样做，复杂度会炸，我们可以只考虑变化量。

考虑我们选 \(f_i \to f_{i+1}\) 的变化，如图：

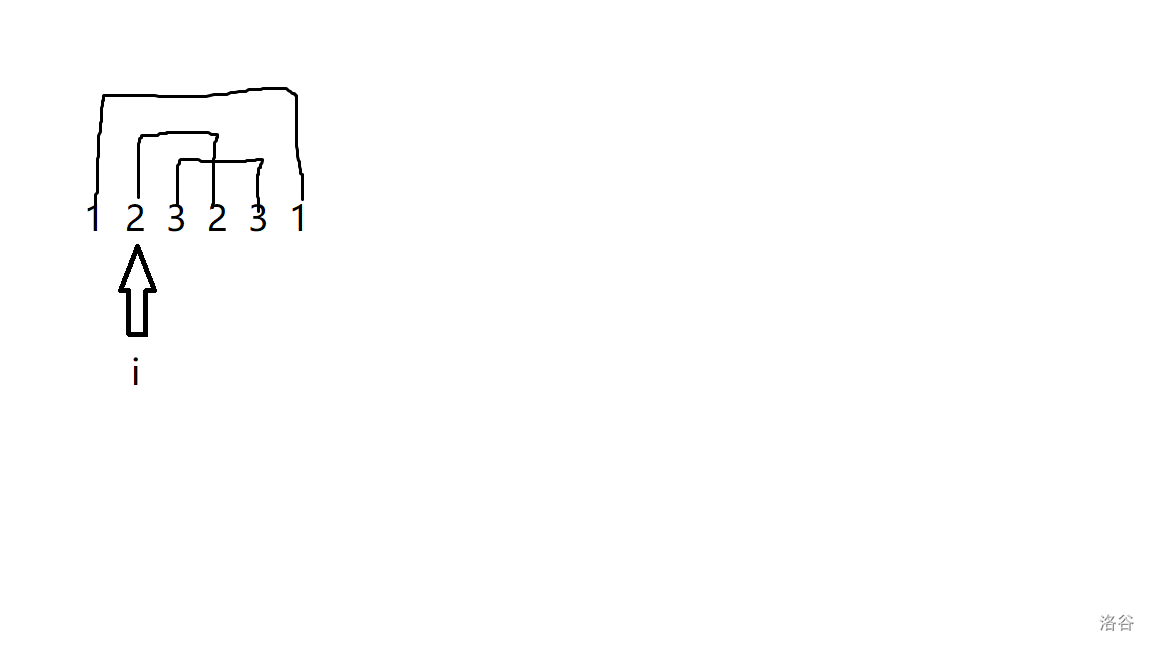
画线的三段区间为进行区间加的区间，如果我们只考虑变化的话，那么对于 \(i=2\)，往后转移时，会加上 \(i=3\) 往后的第一个相等的 \(3\)，进行区间减，对于 \(i=2\) 往前的第一个相等的 \(2\)（未找到），进行区间加（抵消之前区间减的影响，因为当我们把线防止 \(i=3,i+1=4\) 之间时，之前在 \(i=2\) 以前的区间减都无法影响到当前状态），我们需要记录一个值，表示进行区间减前的当前值和进行区间减后的最大值表示当前的权值，最后只要统计上答案即可。

最后代码：Submissions-63843860