NLP随记

NLP Note

线性神经网络

• 搞一个损失函数，然后用梯度下降的方法，不断修改自己的参数，使得损失函数最小，即最贴近实际情况
• 梯度下降：每次往一个梯度最大的方向移动一个步长的大小

多层感知机

• 相比于线性神经网络，加入了隐藏层（激活函数），引入了非线性变化，使得模型可以拟合一些非线性的情况
• Softmax 是一种常用于分类任务中的激活函数，特别是在多类分类问题中，它将网络的输出（通常是一个实数值向量）转换为一个概率分布，使得每个输出值都可以解释为属于某一类别的概率。它通常用于神经网络的最后一层，尤其是在进行多分类任务时。

数学形式

给定一个实数向量 $ z = [z_1, z_2, ..., z_n] $，softmax 函数的输出 $ \text{softmax}(z) $ 是通过以下公式计算的：

\[\text{softmax}(z*i) = \frac{e^{z_i}}{\sum*{j=1}^{n} e^{z_j}} \quad \text{for each} \quad i = 1, 2, ..., n \]

其中：

• $ z_i $ 是原始的网络输出（通常是得分或 logits）。
• $ e^{z_i} $ 是对每个得分进行指数运算。
• $ \sum_{j=1}^{n} e^{z_j} $ 是所有类别得分的指数和，用于归一化结果。

特性

1. 输出为概率：softmax 的输出是一个概率分布，即每个输出值都在 0 和 1 之间，且所有输出值之和为 1：

   \[\sum\_{i=1}^{n} \text{softmax}(z_i) = 1 \]

   这使得每个输出值可以解释为输入数据属于每个类别的概率。

2. 指数放大差异：由于 softmax 对输入值进行了指数运算，它放大了较大的输入得分与较小输入得分之间的差异。因此，softmax 倾向于将高得分的类别预测为最终的类别。

3. 适用于多分类问题：softmax 通常用于多分类任务中的输出层，其中每个类别的概率是独立计算的。它的输出有助于进行最大似然估计（MLE）优化，即通过最大化正确类别的概率来训练模型。

示例

假设一个神经网络的输出是三个类别的得分 $ z = [2.0, 1.0, 0.1] $，softmax 计算如下：

1. 对每个得分进行指数化：

   \[e^{2.0} \approx 7.389, \quad e^{1.0} \approx 2.718, \quad e^{0.1} \approx 1.105 \]

2. 计算总和：

   \[7.389 + 2.718 + 1.105 = 11.212 \]

3. 计算每个类别的 softmax 值：

   \[\text{softmax}(z_1) = \frac{7.389}{11.212} \approx 0.659 \]
   \[\text{softmax}(z_2) = \frac{2.718}{11.212} \approx 0.242 \]
   \[\text{softmax}(z_3) = \frac{1.105}{11.212} \approx 0.099 \]

输出概率为 \([0.659, 0.242, 0.099]\)，表示模型预测类别 1 的概率最高。

应用

• 分类问题：softmax 常用于神经网络的最后一层，尤其是在图像分类、文本分类等任务中。

• 生成概率分布：通过将原始得分转化为概率，softmax 使得模型的输出能够解释为每个类别的可能性。

总之，softmax 是一种将神经网络的输出转化为概率分布的重要方法，是多分类任务中常见的激活函数。

卷积神经网络

• 相比于线性神经网络，卷积神经网络可以学习到数据之间的一些相关的特征，且可以学习到平移不变特征；线性神经网络很难学习到发生位移的物品。
• 卷积层、池化层以及全连接层。
• 卷积层：
  • 提取特征
• 池化层：
  • 压缩特征，如最大池化：在一个范围内留下最大的数，即最重要的特征
  • 池化（Pooling） 是卷积神经网络（CNN）中的一种重要操作，用于下采样（减少数据维度）和压缩特征图（feature map），从而减小计算量、控制过拟合，并提高模型的鲁棒性。池化层通常位于卷积层后面。

池化的主要作用是通过聚合局部区域的信息，减少特征图的尺寸，保留重要的特征，同时丢弃一些不重要的细节。

池化的常见类型

1. 最大池化（Max Pooling）：

   • 最大池化是最常见的池化方法，具体做法是对于输入特征图中的每个局部区域（通常是一个 2x2 或 3x3 的区域），取该区域内的最大值作为输出。
   • 优点：最大池化能够保留该局部区域中的“显著特征”，如边缘和角点等。这对于保持图像的关键特征非常有效。

   例子：
   假设一个 3x3 的输入区域：

   1  3  2
   4  6  5
   7  9  8
   

   进行 2x2 最大池化操作，结果是：

   6  9
   

   通过选择每个 2x2 区域中的最大值（如左上角区域选择 4，右下角区域选择 9），池化操作将特征图的尺寸减少了一半。

2. 平均池化（Average Pooling）：

   • 平均池化操作是取每个局部区域的平均值作为输出。这种方法较为平滑，适用于一些不需要过于强调局部显著特征的任务。
   • 优点：平均池化相比最大池化能更好地捕捉整个区域的信息，而不只是关注局部的“显著特征”。

   例子：
   假设同样的 3x3 输入区域：

   1  3  2
   4  6  5
   7  9  8
   

   进行 2x2 平均池化操作，结果是：

   4.5  6.5
   

   这里每个区域的值是该区域元素的平均值（例如左上角区域的平均值是 (1+3+4+6)/4 = 3.5）。

3. 全局池化（Global Pooling）：

   • 全局池化是池化的一个特例，通常用于将整个特征图（不再是局部区域）映射为一个单一值。比如，全局最大池化会返回整个特征图中的最大值，全局平均池化则会返回整个特征图的平均值。
   • 优点：全局池化可以将特征图的尺寸减少到 1x1，极大地降低了参数量，常用于网络的最后几层。

池化的作用

1. 降低计算量和内存需求：
   池化操作通过减小特征图的尺寸，减少了网络的计算量和内存占用。假设有一个尺寸为 \(32 \times 32 \times 3\) 的输入图像，经过多个卷积和池化层后，特征图的尺寸可能会逐渐缩小（例如缩小到 \(4 \times 4 \times 256\)），这意味着需要计算的参数和特征值大大减少。

2. 减少过拟合：
   池化引入了平移不变性（Translation Invariance）。它通过汇聚局部信息，去掉了对图像中微小变动的敏感性，帮助网络在面对图像的平移、旋转或缩放等变换时，保持较好的鲁棒性。因此，池化有助于防止模型对训练数据的过拟合。

3. 增强特征的鲁棒性：
   池化层能够提取抽象特征并增强其鲁棒性。例如，在最大池化的情况下，网络能够关注图像中的最显著部分而忽略较小的细节，进一步增强对关键特征的识别能力。

4. 帮助训练更深的网络：
   随着网络深度的增加，池化层通过减少特征图的尺寸，帮助网络逐步构建高层次的抽象特征。更深的网络可以聚焦于图像的整体结构而非细节，增强了网络在复杂任务上的表现。

池化层的主要作用是通过减少特征图的尺寸、降低计算量和内存需求，并且帮助增强模型的鲁棒性。常用的池化操作有最大池化和平均池化，它们能够提取图像中的显著特征或平均特征，帮助网络更好地进行学习和预测。池化层在卷积神经网络中扮演着至关重要的角色，尤其是在处理大规模图像时。

• 全连接层：
  • 用于将卷积层和池化层提取到的特征进一步转换为最终的输出。具体来说，全连接层是用于将卷积层提取到的高维特征映射成一个固定的输出（例如，分类任务中的类别概率）。

残差网络

• 先前的网络没办法保证每次学习会更靠近答案，拟合的函数是 H（x）
• 残差网络拟合 H（x）-x， 即尝试拟合目标函数与当前位置的差值
• 可以有效减少梯度爆炸和梯度消失的问题，因为梯度可以跳跃一些层，直接传递回来，使得反向传播的时候不容易出现突然变得极大或突然变得极小的情况
• 因此也可以训练特别深的网络

稠密连接网络

• 每一层连接到之前链接的所有层，利用了所有层的特征，计算量大，运算速度慢，但是反向传播的效率更高，进一步解决了梯度消失问题。
• 参数更少，表现力更强
• 比如残差网络最后训练出来 100 个低等特征表示目标，稠密连接网络可能用 10 个特征就可以表示目标了，但谁最后表现得更像不好说。

循环神经网络（RNN）

• 在多层感知机的基础上，每一步会保存一个时间隐藏变量并更新一个相应的权重矩阵，然后每一步的输出会有这个时间隐藏变量和相应的权重矩阵的参与。

门控循环单元（GRU）（GRN）

• 两个门，重置门和更新门

当然可以。让我们通过一个简单的例子来直观理解重置门（reset gate）、更新门（update gate）以及当前状态（hidden state）的变化。

• 输入数据 $ x_t $：当前时间步的输入（如一个向量）。
• 前一时刻的隐藏状态 $ h_{t-1} $：上一时间步的隐藏状态。
• 重置门 $ r_t $：控制忘记多少前一时刻的状态。
• 更新门 $ z_t $：控制保留多少前一时刻的状态。
• 候选状态 $ \hat{h}_t $：基于当前输入和前一时刻隐藏状态计算出的潜在状态。

步骤 1：计算候选状态 $ \hat{h}_t $

候选状态 $ \hat{h}t $ 是基于当前输入 $ x_t $ 和加权后的前一时刻隐藏状态 $ h $（经重置门调整）计算的。假设我们有权重矩阵 $ W_h $ 和 $ U_h $：

\[\hat{h}_t = \tanh(W_h x_t + U_h (r_t \odot h_{t-1})) \]

步骤 2：计算最终的隐藏状态 $ h_t $

最终的隐藏状态 $ ht $ 是由更新门 $ z_t $ 控制的，它是前一时刻状态 $ h $ 和候选状态 $ \hat{h}_t $ 的加权平均。

\[h*t = z_t \odot h*{t-1} + (1 - z_t) \odot \hat{h}\_t \]

• 重置门（reset gate）决定了我们“忘记”前一时刻隐藏状态的多少。
• 更新门（update gate）决定了我们“混合”前一时刻状态与新信息的比例，从而控制当前时刻的最终状态。

GRU 的这种门控机制使得它能够在长期序列中有效地学习和记忆关键信息，避免了传统 RNN 中的梯度消失问题。

LSTM

• 多了遗忘门、输入门、输出门

LSTM（长短期记忆网络，Long Short-Term Memory）通过一系列的门（gate）机制来控制信息的流动，解决传统 RNN 在长序列中遇到的梯度消失和梯度爆炸问题。LSTM 的核心是它的 记忆单元（cell state），门限机制决定了哪些信息应该保留、更新或遗忘。

以下是 LSTM 的门限工作机制的详细解释：

---

1. LSTM 的基本结构

每个 LSTM 单元包含三个主要的门限：

1. 遗忘门（Forget Gate）：决定当前时刻是否“遗忘”先前记忆。
2. 输入门（Input Gate）：决定当前时刻是否将新的信息写入记忆单元。
3. 输出门（Output Gate）：决定当前时刻是否将记忆单元的信息输出。

这些门通过逻辑控制信息的流动，从而调整 LSTM 的记忆状态。

---

2. LSTM 的计算流程

2.1 遗忘门（Forget Gate）

• 目的：控制是否遗忘之前的记忆。

• 公式：

  \[f*t = \sigma(W_f \cdot [h*{t-1}, x_t] + b_f) \]
  • $ f_t $ 是遗忘门的输出（一个向量，每个值在 $ [0, 1] $ 之间）。
  • $ W_f $ 和 $ b_f $ 是遗忘门的权重和偏置。
  • $ h_{t-1} $ 是上一时间步的隐藏状态。
  • $ x_t $ 是当前时间步的输入。
  • $ \sigma $ 是 Sigmoid 激活函数，输出值控制遗忘程度：
    • $ f_t = 0 $：完全遗忘；
    • $ f_t = 1 $：完全保留。

• 作用：通过 $ ft $ 的值，将前一个时间步的记忆 $ C $ 进行选择性保留或遗忘：

  \[C\_{t-1} \cdot f_t \]

2.2 输入门（Input Gate）

• 目的：决定当前时刻有多少新信息被写入记忆单元。

• 公式：

  • 输入门控制：

    \[i*t = \sigma(W_i \cdot [h*{t-1}, x_t] + b_i) \]
    • $ i_t $ 是输入门的输出（每个值在 $ [0, 1] $ 之间）。
    • $ W_i $ 和 $ b_i $ 是输入门的权重和偏置。

  • 候选记忆单元更新：

    \[\tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C) \]
    • $ \tilde{C}_t $ 是当前时刻的候选记忆。
    • $ \tanh $ 激活函数将值限制在 $ [-1, 1] $ 范围内。

• 作用：输入门决定新信息如何更新记忆单元：

  \[C*t = f_t \cdot C*{t-1} + i_t \cdot \tilde{C}\_t \]
  • $ ft \cdot C $：保留的旧记忆。
  • $ i_t \cdot \tilde{C}_t $：加入的新信息。

2.3 输出门（Output Gate）

• 目的：决定当前时刻从记忆单元中输出多少信息。

• 公式：

  \[o*t = \sigma(W_o \cdot [h*{t-1}, x_t] + b_o) \]
  • $ o_t $ 是输出门的输出（每个值在 $ [0, 1] $ 之间）。
  • $ W_o $ 和 $ b_o $ 是输出门的权重和偏置。

• 作用：结合记忆单元的状态 $ C_t $，通过 $ \tanh $ 激活函数，输出隐藏状态 $ h_t $：

  \[h_t = o_t \cdot \tanh(C_t) \]
  • $ \tanh(C_t) $：记忆单元状态的非线性映射。
  • $ o_t $：控制最终输出信息的比例。

---

3. LSTM 的核心状态更新

LSTM 的设计通过上述三个门实现了对记忆单元的灵活控制：

1. 遗忘门决定要“清理”哪些旧信息。
2. 输入门决定要写入哪些新信息。
3. 输出门决定从记忆中输出哪些信息。

最终的记忆状态更新公式为：

\[C*t = f_t \cdot C*{t-1} + i_t \cdot \tilde{C}\_t \]

隐藏状态（输出）为：

\[h_t = o_t \cdot \tanh(C_t) \]

---

4. 举例说明

假设我们有一个简单的时间序列任务，输入 $ x_t $ 是温度数据（例如 25°C、26°C 等）。目标是预测下一时刻的温度趋势（升高、降低或持平）。

时间步 $ t-1 $

• $ C_{t-1} $：记忆单元中存储了之前温度变化的趋势。

• $ h_{t-1} $：隐藏状态代表短期上下文信息。

当前时间步 $ t $

• 当前输入 $ x_t = 26 $（当前温度）。

• 遗忘门：
  • $ f_t $：判断是否保留之前的趋势。
  • 如果过去的温度变化已经过时，遗忘门可能输出较低值（如 $ f_t = 0.2 $）。
• 输入门：
  • $ i_t $：决定是否将新的温度信息写入记忆单元。
  • 如果当前温度有显著变化（如从 25°C 升到 26°C），输入门可能输出较高值（如 $ i_t = 0.8 $）。
  • 候选记忆单元 $ \tilde{C}_t $：可能存储当前温度变化趋势。
• 输出门：
  • $ o_t $：根据记忆单元的内容，决定输出多少信息。
  • 如果当前趋势较重要，输出门可能输出较高值（如 $ o_t = 0.9 $）。

状态更新

• 记忆单元更新：
  \[C*t = f_t \cdot C*{t-1} + i_t \cdot \tilde{C}\_t \]

• 隐藏状态更新：
  \[h_t = o_t \cdot \tanh(C_t) \]

最终，LSTM 会结合当前输入 $ xt $、过去的隐藏状态 $ h $ 和记忆单元 $ C_{t-1} $，输出一个隐藏状态 $ h_t $，用于预测下一个时间步的趋势。

---

5. LSTM 门限的关键优点

1. 长期记忆和短期记忆的结合：
   • 遗忘门让 LSTM 可以选择性遗忘过时信息。
   • 输入门允许写入新的重要信息。
2. 避免梯度消失：
   • 记忆单元中的线性累积（通过加法操作）保留了长期信息，不会像传统 RNN 那样因梯度消失而无法更新。
3. 灵活的控制机制：
   • 门限机制提供了更精细的控制，可以根据任务需求动态调整记忆和输出。

LSTM 的门限机制通过 遗忘门、输入门和输出门 精确控制记忆单元中的信息流动：

• 遗忘门决定删除哪些旧信息。
• 输入门决定添加哪些新信息。
• 输出门决定输出哪些信息给隐藏状态。

RAG

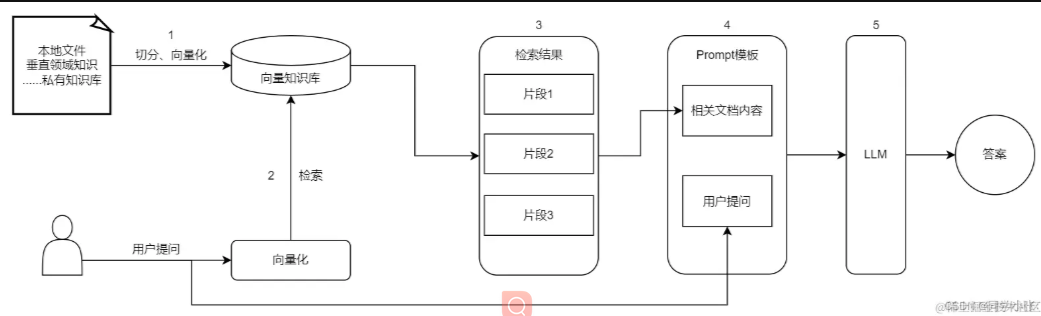
这个检索常用的方式有对比相似度
检索到后，吧匹配到的片段直接塞入 prompt 模板，和用户提问一起丢给 LLM

Transformer 能够“战胜”RNN、LSTM、GRU 等架构，主要是依靠它的并行计算、长距离建模、大容量、强泛化等能力，这些能力让它能够更好的适应现代的硬件水平，面对大规模数据时，实现较高的训练效率。

	循环神经网络 (RNN)	长短期记忆网络 (LSTM)	门控循环单元 (GRU)	Transformer
概述	RNN 是基础序列模型，通过迭代处理序列，使用前一步的输出作为当前步骤的输入。	LSTM 是标准 RNN 的增强版，能够更好的捕捉序列中的长期依赖关系。	GRU 是 LSTM 的一种变体，具有简化的门控机制。	Transformer 摒弃了循环结构，专注于自注意力机制来并行处理数据。
主要特征	循环连接允许保留来自先前时间步的“记忆”。	使用门（输入、遗忘和输出门）来调节信息流。除隐藏状态外，还有一个单元状态来携带长序列的相关信息。	包含两个门：重置门和更新门。2. 合并单元状态和隐藏状态。	使用自注意力机制来权衡输入数据的不同部分的重要性。2. 由多个编码器和解码器块组成。3. 并行处理数据而不是顺序处理。
优点	结构简单适用于短序列任务。	能捕获和记住数据中的长期依赖关系。2.缓解了 RNN 的梯度消失问题。	参数比 LSTM 少，训练时间更短。结构简化但仍保留捕获长期依赖的能力。	无需依赖循环即可捕获长距离依赖关系。高度可并行化，在合适的硬件上训练更快。
缺点	1.存在梯度消失和爆炸问题，难以学习长期依赖关系。2. 记忆跨度有限。	计算密度比 RNN 高。复杂性可能导致更长的训练时间。	在某些任务中可能无法像 LSTM 那样有效地捕获长期依赖关系。	需要大量数据和计算能力进行训练。由于注意力机制，可能在处理长序列时需要大量内存。
应用案例	由于各种局限性，普通 RNN 在现代应用中较少使用。一般只用于简单的语言建模、时间序列预测。	机器翻译、语音识别、情感分析，以及其他需要理解长期上下文的任务。	文本生成、情感分析和其他模型效率是优先考虑的序列任务。	各种 NLP 任务，包括机器翻译、文本摘要等，是 BERT 和 GPT 等大模型的基本架构。
模型变体	原始 RNN、双向 RNN、深度（堆叠）RNN 等	原始 LSTM、双向 LSTM、窥孔 LSTM、深度（堆叠）LSTM	GRU	原始 Transformer（Seq-to-Seq）、仅编码器（如：BERT）、仅解码器（如：GPT）、文本到文本

从这些总结可以看出，普通 RNN 结构简单，适用于短序列，难以捕捉长期依赖，所以在目前数据量越来越庞大的情况下，应用受限；

LSTM 通过门机制，一定程度的克服了 RNN 的局限性，能够处理长序列依赖，在机器翻译等任务中表现出色，但复杂度和训练时间也有所增加；

GRU 则是在 LSTM 的基础上做了简化，提高了训练效率，但是在某些任务上无法取得与 LSTM 相近的效果。

自然而然的，拥有强大的并行计算能力、长程依赖建模、海量数据训练等优势的 Transformer“脱颖而出”，逐渐成为近年来 NLP 领域的主流架构。

不过 Transformer 也并非完美，它对算力和数据量要求很高，而且并非所有任务都适合使用 Transformer。

强化学习

RNN， LSTM， Transformer 都属于神经网络，属于深度学习

强化学习指的是只给出一个结果，让机器自己去寻找最优策略。
强化学习算法有 PPO，DPO，GRPO

PPO

(1) 环境采样：Policy Model 基于给定输入生成一系列的回复，Reward Model 则对这些回复进行打分获得奖励。
(2) 优势估计：利用 Critic Model，预测生成回复的未来累积奖励，并借助广义优势估计（Generalized Advantage Estimation，GAE）算法来估计优势函数，能够有助于更准确地评估每次行动的好处。
(3) 优化调整：使用优势函数来优化和调整 Policy Model，同时利用 Reference Model 确保更新的策略不会有太大的变化，从而维持模型的稳定性。

DPO

• 不包含奖励模型和强化学习过程，直接通过偏好数据进行微调，将强化学习过程之间转化为 SFT（监督微调）过程，训练简单高效。
• 利用奖励模型与最优策略之间的映射关系，证明这个受限的奖励最大化问题可以通过单阶段的策略训练来精确优化，本质上是在人类偏好数据上解决一个分类问题。
• 分区函数 Z(x) 在 PPO 中起到归一化的作用，确保概率分布 \(\pi^*(y|x)\) 的合法性（概率和为 1）。DPO 直接省略了分区函数，假设 \(\pi_\text{ref}(y|x)\) 已经足够准确地反映了所有选择的分布。然而，当参考分布 \(\pi_\text{ref}(y|x)\) 不够准确时，这种省略可能导致对某些选项（例如偏好数据不足的选项）赋予不合理的高权重。

微调

Lora

PERT（参数高效微调）的一种形式

• 学习变化矩阵的因子
• Lora 不直接记载需要修改的地方，而是记载修改的方式
• 修改方式（Change Matrix）很有可能是线性相关的，因此可以分解成两个低秩的因子。

步骤：

1. 冻结所有参数，作为一个参考，不会更新他们
2. 设置微调矩阵 A 和 B，分别是原先参数矩阵的长和宽
3. A 和 B 乘起来规模和原先参数矩阵一致
4. 乘起来后和原先的参数矩阵相加输出，然后反向传播微调 A 和 B
   

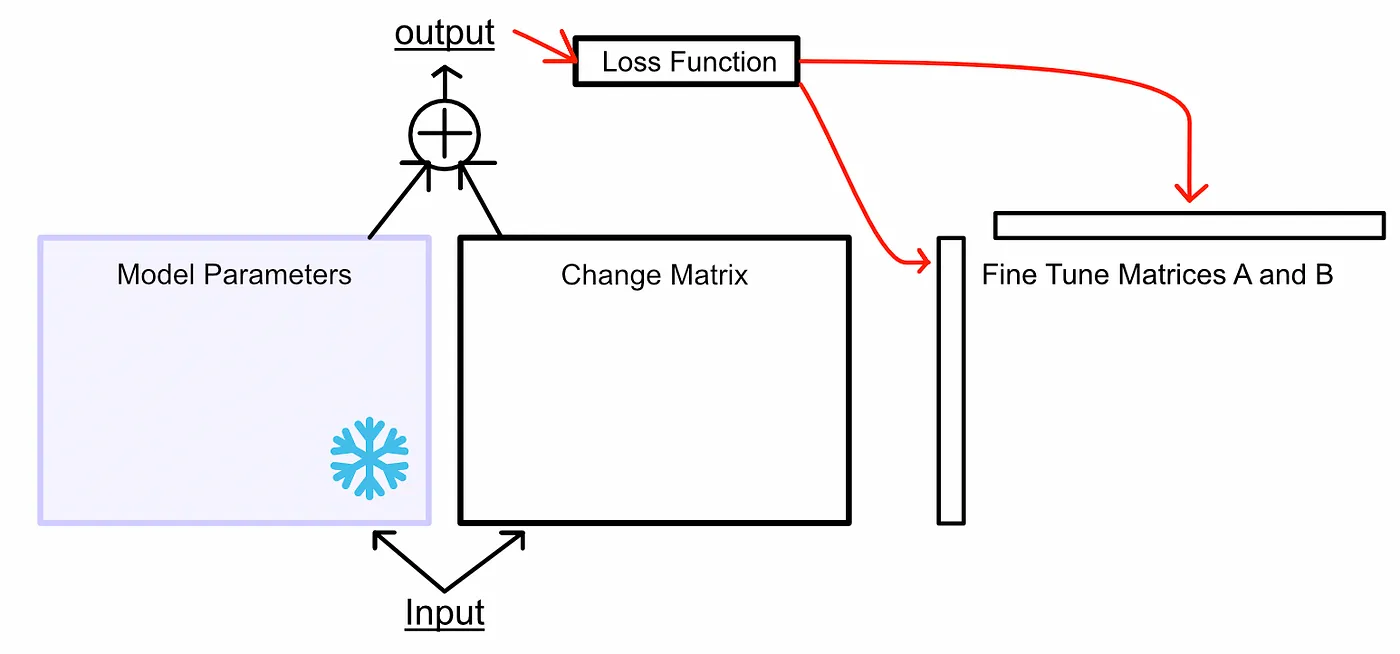
拥有一个超参数 r，指的是 A 和 B 的宽度，通常设为 1 就会有不错的效果

Qlora

量化后的微调

• 模型量化
  • 模型的低精度表示，如 float 到 int

1. 分位数量化

• 按照概率分布，量化掉概率比较小的部分

Transformer

Attention 层

• 词汇表训练好后每个单词会表示成一个向量，这个向量的各个维度和这个词本身包含的意思高度相关。不同单词的向量之间表示了不同词之间的关系

• 然后把目前的句子丢入 transformer，

softmax(QK^T/根号 d)V

• Q
  • 训练好后，每一个词的 Q 会知道它需要关注哪些属性的词
• K
  • 训练好后，每一个词的 K 代表它可能会被关注到的属性
• V
  • 训练好后，每一个词的 V 代表它会产生的影响大小（权重）

这三个属性都是用于最大程度展示词向量的特点的，不一定要是这种构造，但是这种构造（正方形，自乘）可以最大化特征。

MLP

FFN，前向反馈网络，算是一种多层感知机，包含三个步骤：

• 升维
  • 使用一个高维的矩阵乘以我们提出的向量，每一行就好像提出一个问题，这一层的结果就是对于每个问题的答案（好像是，有很大可能是，应该不是）
    
• 激活层
  • RELU，语言是非线性的，我们需要的是一个准确的 yes or no，而不是相关的概念（是，或者不是），这一层的结果表示要往最终的结果里添加哪些内容
• 降维
  • 把提取到的特征结合到一起，形成一个新的事物。每一个事物都是由向量组成的，每一维代表了一个特征，所有事物都可以用这些特征表示（是不是语言，是不是动物，英语还是俄文，名词还是动词）

最终的用处是，输入麦克乔丹，输出篮球。

attention 层主要用于结合上下文，将词修正为词在句子中的真正意思；
MLP 层是主要的推理层，负责结合上文推理出下文

训练：

• 使用反向传播直接训练

• 训练的过程，一句话，可以同时预测每一个子串后面需要接上的 token

• 如 “今天天气真好”，同时训练

  • 今？

  • 今天？

  • 今天天？

  • 这种情况需要对后面的词做掩码，防止注意力网络提前看到答案，可以在 softmax 前设为负无穷，这样 softmax 后就为 0 了。