第四章贪心算法上机实验报告

4-1 程序存储问题 (40 分)

设有n 个程序{1,2,…, n }要存放在长度为L的磁带上。程序i存放在磁带上的长度是 li，1≤i≤n。程序存储问题要求确定这n 个程序在磁带上的一个存储方案，使得能够在磁带上存储尽可能多的程序。对于给定的n个程序存放在磁带上的长度，计算磁带上最多可以存储的程序数。

输入格式:

第一行是2 个正整数，分别表示文件个数n和磁带的长度L。接下来的1行中，有n个正整数，表示程序存放在磁带上的长度。

输出格式:

输出最多可以存储的程序数。

输入样例:

在这里给出一组输入。例如：

6 50 
2 3 13 8 80 20

结尾无空行

输出样例:

在这里给出相应的输出。例如：

结尾无空行

分析：

•要找到一个能放置最多程序的方案

思路：

•要想在固定空间大小的磁带上存放尽可能多的程序，需要尽可能的放小的程序，这样子才能充分利用空间

•可以对程序大小进行升序排序，然后逐个将程序放入磁带中，知道放不下为止

时间复杂度：

•排序sort：O（n）= nlogn

•选择：O（n）= n

复杂度为nlogn

代码：

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 int main(){
 5     int space, num, a[1000];
 6     cin >> num >> space;
 7     
 8     for(int i = 0; i < num; i++){
 9         cin >> a[i];
10     }
11     
12     sort(a, a+num);
13     int flag = 0;
14     while(space > 0){
15         if(space >= a[flag]){
16             space -= a[flag];
17             flag++;
18         }else break;
19         
20     }
21     
22     cout << flag << endl;
23 }

4-2 删数问题 (30 分)

给定n位正整数a，去掉其中任意k≤n 个数字后，剩下的数字按原次序排列组成一个新的正整数。对于给定的n位正整数a和正整数 k，设计一个算法找出剩下数字组成的新数最小的删数方案。如果数字最前面有0不输出。

输入格式:

第 1 行是1 个正整数 a。第 2 行是正整数k。

输出格式:

输出最小数。

输入样例:

在这里给出一组输入。例如：

178543 
4

结尾无空行

5001 
1

结尾无空行

123456 
2

结尾无空行

109 
1

结尾无空行

输出样例:

在这里给出相应的输出。例如：

结尾无空行

分析：

•按照原次序的基础上进行删除

•每次删除的数字为第一个寻找到的峰值

思路：

•可以将原题目中的数字当作字符串来处理（因为字符之间的大小也可以直接比较）

•每次找到一个峰值就将这个峰值删掉，可以用string.erase()函数删除峰值

时间复杂度：

•最坏情况下就是每次都删除最后一个数（1234567删一个就是7），每次遍历都要到最后，遍历k遍

•O（n）= （n + （n-k））*k/2 = n

复杂度为n

代码：

 1 #include <iostream>
 2 #include <cstring>
 3 using namespace std;
 4 int main(){
 5     string a;
 6     int k;
 7     cin >> a;
 8     cin >> k;
 9     if(k >= a.length()){
10         a.erase();
11     }else while(k > 0){
12     int i;
13     for( i = 0; i < (a.length()-1) && (a[i] <= a[i+1]); i++);
14     a.erase(i,1);
15     k--;
16     }
17     while(a[0] == '0' && a.length() > 1)
18         a.erase(0,1);
19     
20     
21     cout << a;    
22     return 0;     
23 }

4-3 最优合并问题 (30 分)

题目来源：王晓东《算法设计与分析》

给定k 个排好序的序列, 用 2 路合并算法将这k 个序列合并成一个序列。假设所采用的 2 路合并算法合并 2 个长度分别为m和n的序列需要m+n-1 次比较。试设计一个算法确定合并这个序列的最优合并顺序，使所需的总比较次数最少。为了进行比较，还需要确定合并这个序列的最差合并顺序，使所需的总比较次数最多。

输入格式:

第一行有 1 个正整数k，表示有 k个待合并序列。第二行有 k个正整数，表示 k个待合并序列的长度。

输出格式:

输出最多比较次数和最少比较次数。

输入样例:

在这里给出一组输入。例如：

4
5 12 11 2

结尾无空行

输出样例:

在这里给出相应的输出。例如：

78 52

结尾无空行

分析：

•每次合并两个序列n和m就会产生一个新的序列n+m继续参与合并，比较次数n+m-1

•新的序列n+m与o参与合并，比较次数n+m+o-1，可以发现前面序列的数被重复利用，要想最大或最小，就得让重复的数尽可能的大或者小

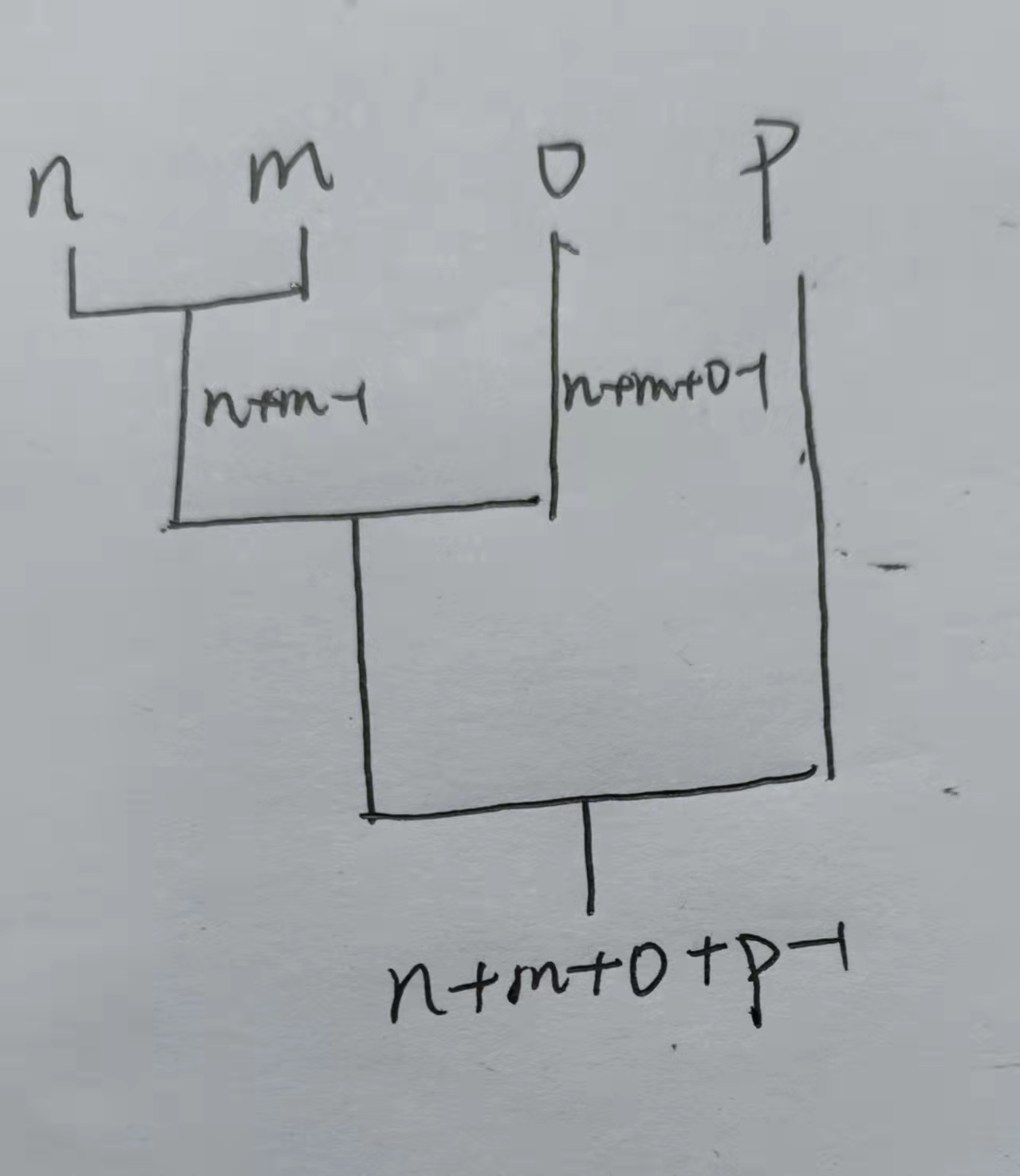
思路：

•可以使用两个优先队列来实现（默认大顶堆）一个大顶堆和一个小顶堆，

队头两个元素合并插入合并之后的序列进入队尾直到合并为1个序列

时间复杂度：

•选择：O（n）= n

复杂度为n

代码：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int main()
 4 {
 5     priority_queue<int,vector<int>,greater<int> >q1;
 6     priority_queue<int>q2;
 7     int n;
 8     cin>>n;
 9     for(int i =0; i<n; i++)
10     {
11         int x;
12         cin>>x;
13         q1.push(x);
14         q2.push(x);
15     }
16     int max =0,min =0;
17     while(q1.size()>1)
18     {
19 
20         int a =q1.top();
21         q1.pop();
22         int b =q1.top();
23         q1.pop();
24         min +=a+b-1;
25         q1.push(a+b);
26 
27     }
28 
29     while(q2.size()>1)
30     {
31 
32         int a =q2.top();
33         q2.pop();
34         int b =q2.top();
35         q2.pop();
36         max +=a+b-1;
37         q2.push(a+b);
38 
39     }
40     cout<< max <<" "<< min <<endl;
41     return 0;
42 }

贪心算法个人观点：

　　贪心人人生而俱来，都是趋向于利益最大化，贪心算法给出当前条件下的最优解，当条件一改变就不保证成立，所以贪心算法给出的是所谓的局部最优解不考虑全局的选择。它不保证能得到整体最优，但也有局部最优是整体最优的情况，这时候就要证明你的局部最优是全局最优。

posted on 2021-11-11 14:57 Aheador 阅读(204) 评论(0) 编辑收藏举报