2.13 --2.15 链表 双叉树
1.链表
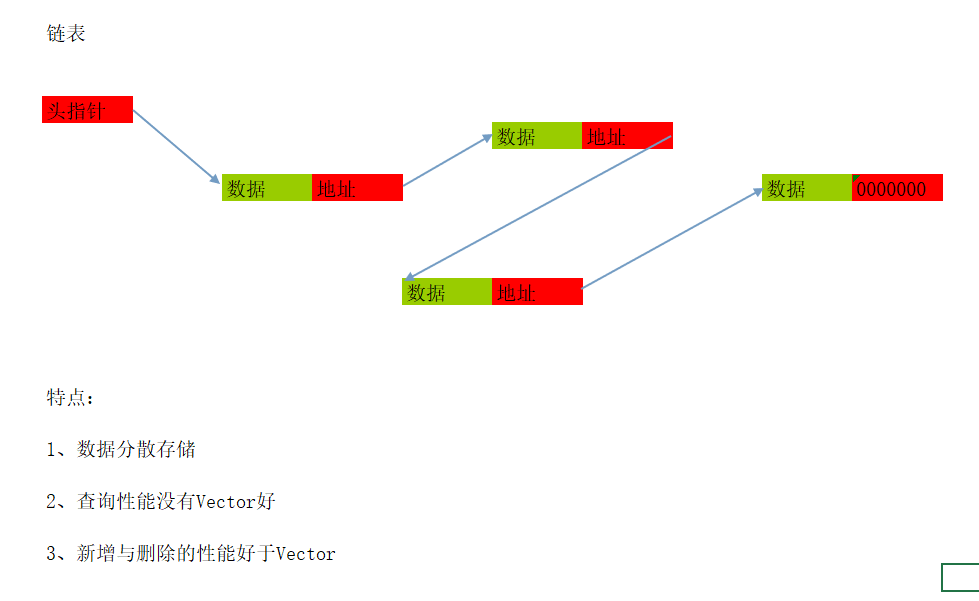
这是单链表
链表大全
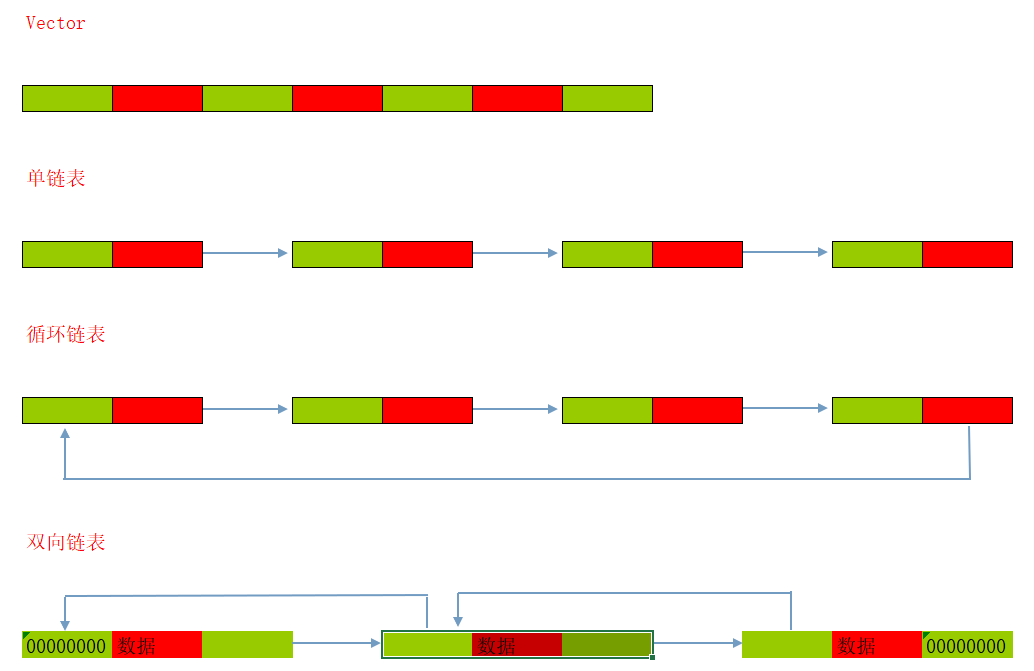
链表代码
点击查看代码
#include<stdio.h>
#include<Windows.h>
#define SUCCESS 1 // 执行成功
#define ERROR -1 // 执行失败
#define INDEX_IS_ERROR -2 // 错误的索引号
#define BUFFER_IS_EMPTY -3 // 缓冲区已空
template<class T_ELE>
class NODE
{
public:
T_ELE Data;
NODE<T_ELE>* pNext;
};
template <class T_ELE>
class LinkedList :public NODE<T_ELE>
{
public:
LinkedList(); //默认构造函数
~LinkedList();
public:
BOOL IsEmpty(); //判断链表是否为空 空返回1 非空返回0
DWORD Clear(); //清空链表
DWORD GetElement(IN DWORD dwIndex, OUT T_ELE& Element); //根据索引获取元素
DWORD GetElementIndex(IN T_ELE& Element); //根据元素获取链表中的索引
DWORD Insert(IN T_ELE Element); //新增元素
DWORD Insert(IN DWORD dwIndex, IN T_ELE Element); //根据索引新增元素
DWORD Delete(IN DWORD dwIndex); //根据索引删除元素
DWORD GetSize(); //获取链表中元素的数量
VOID Show();
private:
NODE<T_ELE>* m_head; //链表头指针,指向第一个节点
NODE<T_ELE>* m_tail;
DWORD m_dwLength; //元素的数量
};
//无参构造函数 初始化成员
template<class T_ELE> LinkedList<T_ELE>::LinkedList()
:m_head(NULL), m_dwLength(0)
{
}
//析构函数 清空元素
template<class T_ELE> LinkedList<T_ELE>::~LinkedList()
{
printf("11");
Clear();
}
//判断链表是否为空
template<class T_ELE> BOOL LinkedList<T_ELE>::IsEmpty()
{
if (m_head == NULL || m_dwLength == 0)
{
return TRUE;
}
else
{
return FALSE;
}
}
//清空链表
template<class T_ELE> DWORD LinkedList<T_ELE>::Clear()
{
// 1. 判断链表是否为空
if (m_head == NULL || m_dwLength == 0)
{
return BUFFER_IS_EMPTY;
}
// 2. 循环删除链表中的节点
NODE<T_ELE>* pTempNode = m_head;
for (DWORD i = 0; i < m_dwLength; i++)
{
NODE<T_ELE>* pIterator = pTempNode;
pTempNode = pTempNode->pNext;
delete pIterator;
}
// 3. 删除最后一个节点并将链表长度置为0
m_head = NULL;
m_dwLength = 0;
return SUCCESS;
}
//根据索引获取元素
template<class T_ELE> DWORD LinkedList<T_ELE>::GetElement(IN DWORD dwIndex, OUT T_ELE& Element)
{
if (dwIndex<0 || dwIndex>m_dwLength)
{
return INDEX_IS_ERROR;
}
NODE<T_ELE>* IO = m_head;
NODE<T_ELE>* to = NULL;
for (int i = 0; i < dwIndex; i++)
{
IO = IO->pNext;
}
memcpy(&Element, &IO->Data, sizeof(T_ELE));
return SUCCESS;
}
//根据元素内容获取索引
template<class T_ELE> DWORD LinkedList<T_ELE>::GetElementIndex(IN T_ELE& Element)
{
// 1. 判断链表是否为空
if (m_head == NULL || m_dwLength == 0)
{
return INDEX_IS_ERROR;
}
NODE<T_ELE>* B = NULL;
B = m_head;
for (int o; o < m_dwLength; 0++)
{
if (memcmp(&Element,&B->Data),sizeof(T_ELE))
{
return o;
}
B = B->pNext;
}
return false;
}
//在链表尾部新增节点
template<class T_ELE> DWORD LinkedList<T_ELE>::Insert(IN T_ELE Element)
{
NODE<T_ELE>* pNewNode = new NODE<T_ELE>;
memset(pNewNode, 0, sizeof(NODE<T_ELE>));
memcpy(&pNewNode->Data, &Element, sizeof(T_ELE));
///节点数据成功
// 1. 判断链表是否为空
if (m_head == NULL || m_dwLength == 0)
{
m_head = pNewNode;
m_dwLength++;
return SUCCESS;
}
// 2. 如果链表中已经有元素
NODE<T_ELE>* pTempNode = m_head;
for (DWORD i = 0; i < m_dwLength - 1; i++)
{
pTempNode = pTempNode->pNext;
}
//依次向下找,直到最后的节点的那个地址
pTempNode->pNext = pNewNode;
m_dwLength++;
return SUCCESS;
}
//将节点新增到指定索引的位置 0 1 2 3 4
template<class T_ELE> DWORD LinkedList<T_ELE>::Insert(IN DWORD dwIndex, IN T_ELE Element)
{
NODE<T_ELE>* pNewNode = new NODE<T_ELE>;
memset(pNewNode, 0, sizeof(T_ELE));
memccpy(&pNewNode, &Element, sizeof(T_ELE));
///链表为空
if (m_head == NULL || m_dwLength == 0)
{
m_head = pNewNode;
m_dwLength++;
return SUCCESS;
}
// 2. 判断索引值是否有效
if (dwIndex > m_dwLength || dwIndex < 0)
{
printf("输入错误");
}
// 3. 如果索引为0
if (dwIndex == 0)
{
NODE<T_ELE>* a = m_head;
pNewNode->pNext = a;
//拿到下个索引的值
m_head = pNewNode;
m_dwLength++;
return SUCCESS;
}
// 4. 如果索引为链表尾
if (dwIndex == m_dwLength)
{
NODE<T_ELE>* ad = m_head;
for (INT i = 0; i < m_dwLength; i++)
{
ad = ad->pNext;
}
ad->pNext = pNewNode;
m_dwLength++;
return SUCCESS;
}
// 5. 如果索引为链表中
//在中间 前后
///前
NODE<T_ELE>* NN = m_head;
for (int i; i < dwIndex-1; i++)
{
NN = NN->pNext;
}
//存储后节点值
NODE<T_ELE>* hou = NN->pNext;
NN->pNext = pNewNode;
pNewNode->pNext = hou;
m_dwLength++;
return SUCCESS;
}
//根据索引删除节点
template<class T_ELE> DWORD LinkedList<T_ELE>::Delete(IN DWORD dwIndex)
{
NODE<T_ELE>* pPreviousNode = NULL;
NODE<T_ELE>* pCurrentNode = NULL;
NODE<T_ELE>* pNextNode = NULL;
// 1. 判断链表是否为空
if (m_head == NULL || m_dwLength == 0)
{
return BUFFER_IS_EMPTY;
}
// 2. 判断索引值是否有效
if (dwIndex > m_dwLength || dwIndex < 0)
{
printf("输入错误");
}
// 3. 如果链表中只有头节点,且要删除头节点
if (m_dwLength == 1 && dwIndex == 0)
{
delete m_head;
m_head = NULL;
m_tail = NULL;
m_dwLength--;
return SUCCESS;
}
// 4. 如果要删除头节点
if (dwIndex == 0)
{
pNextNode = m_head->pNext;
delete m_head;
m_head = pNextNode;
m_dwLength--;
return SUCCESS;
}
// 5. 如果要删除尾节点
if (dwIndex == m_dwLength - 1)
{
pPreviousNode = m_tail->pPre;
delete m_tail;
m_tail = pPreviousNode;
m_dwLength--;
return SUCCESS;
}
// 6. 如果是其他情况
pPreviousNode = m_head;
for (DWORD i = 0; i < dwIndex - 1; i++)
{
pPreviousNode = pPreviousNode->pNext;
}
pCurrentNode = pPreviousNode->pNext;
pNextNode = pCurrentNode->pNext;
pPreviousNode->pNext = pNextNode;
pNextNode->pPre = pPreviousNode;
delete pCurrentNode;
m_dwLength--;
return SUCCESS;
}
//获取链表中节点的数量
template<class T_ELE> DWORD LinkedList<T_ELE>::GetSize()
{
if (m_head == NULL || m_dwLength == 0)
{
return BUFFER_IS_EMPTY;
}
else
{
return m_dwLength;
}
}
template<class T_ELE> VOID LinkedList<T_ELE>::Show()
{
if (m_head == NULL || m_dwLength == 0)
{
printf("Linklist is empty.\n");
return;
}
NODE<T_ELE>* pTempNode = m_head;
for (DWORD i = 0; i < m_dwLength; i++)
{
printf("pNode->data: %d\n", pTempNode->Data);
pTempNode = pTempNode->pNext;
}
}
VOID TestLink()
{
LinkedList<int> Link;
Link.Insert(3);
Link.Insert(3);
Link.Insert(6);
int a = 0;
Link.GetElement(2,a);
printf("大小:%d", a);
printf("%d", Link.GetSize());
}
int main()
{
TestLink();
return 0;
}
二叉树
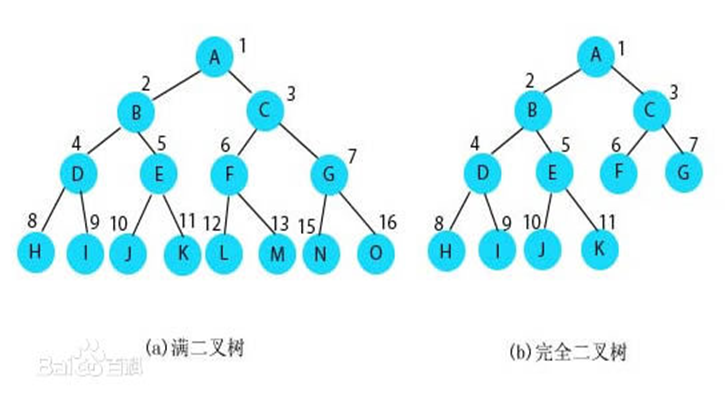
1.二叉树性质
根节点
父节点
字节点
左子树
右子树
这些性质是相对而言
2.二叉树的高度
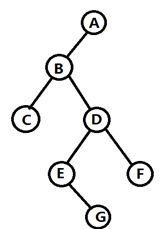
二叉树的高度也是相对而言 图中的高度为5
3.二叉树的遍历
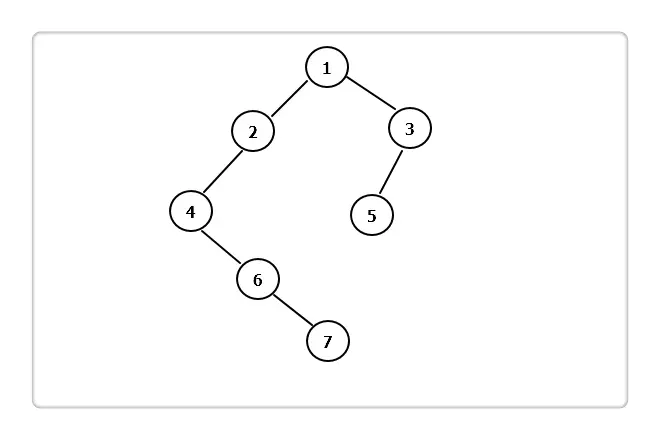
前序遍历:(根 左 右)
1 2 4 6 7 3 5
中序遍历:(左 根 右)
对于当前结点,先输出它的左孩子,然后输出该结点,最后输出它的右孩子。以上图为例:
左树 为 2 开始遍历 4 -6-7 -2 左树遍历完成
根 1
3-的左节点 为5
右 5-3
4.后序遍历
左右根
7-6-4-2
5-3
1
遍历代码
https://img-blog.csdnimg.cn/d39c11182d0f485f8e3d194fe4c8340e.png
前
A B D E G C F
中
左
B-D D左右树为空 输出 D
回B B左树为空 输出B
E-G 左节点为 G 根为 E
D B G E
左树遍历完成
根 A
C无左树 输出C F
DBGEACF
后序排列
B -D -D
B-E-G G E
D G E B
C-F F C
A
D G E B F C A
查找代码
点击查看代码
#include<stdio.h>
#include<Windows.h>
class Monster
{
public:
int ID;
int Level;
char Name[20];
public:
Monster() {}
Monster(int ID, int Level, char* Name)
{
this->ID = ID;
this->Level = Level;
memcpy(&this->Name, Name, strlen(Name) + 1);
}
};
template<class T>
class TreeNode {
public:
T element; //当前节点存储的数据
TreeNode<T>* pLeft; //指向左子节点的指针
TreeNode<T>* pRight; //指向右子节点的指针
TreeNode(T& ele) {
//初始化Node节点
memset(&element, 0, sizeof(TreeNode));
//为元素赋值
memcpy(&element, &ele, sizeof(T));
pLeft = pRight = NULL;
}
};
template<class T>
class BSortTree {
public:
BSortTree(); //构造函数
~BSortTree(); //析构函数
public:
void InOrderTraverse(TreeNode<T>* pNode); //中序遍历
void PreOrderTraverse(TreeNode<T>* pNode); //前序遍历
void PostOrderTraverse(TreeNode<T>* pNode); //后序遍历
TreeNode<T>* GetRoot(); //返回根节点
int GetDepth(TreeNode<T>* pNode); //返回某个节点的高度/深度
private:
void Init();
void Destory(TreeNode<T>* pNode);
private:
TreeNode<T>* m_pRoot; //根结点指针
int size; //树中元素总个数
};
template<class T>
BSortTree<T>::BSortTree()
{
Init();
}
template<class T>
BSortTree<T>::~BSortTree()
{
printf("Destory function...\n");
Destory(m_pRoot);
}
template<class T>
void BSortTree<T>::Destory(TreeNode<T>* pNode)
{
//释放所有节点空间
if (pNode == NULL)
{
return;
}
else
{
Destory(pNode->pLeft);
Destory(pNode->pRight);
delete pNode;
pNode = NULL;
}
}
template<class T>
void BSortTree<T>::Init()
{
Monster m1(1, 1, (char*)"1");
Monster m2(2, 2, (char*)"2");
Monster m3(3, 3, (char*)"3");
Monster m4(4, 4, (char*)"4");
Monster m5(5, 5, (char*)"5");
Monster m6(6, 6, (char*)"6");
Monster m7(7, 7, (char*)"7");
TreeNode<Monster>* n1 = new TreeNode<Monster>(m1);
TreeNode<Monster>* n2 = new TreeNode<Monster>(m2);
TreeNode<Monster>* n3 = new TreeNode<Monster>(m3);
TreeNode<Monster>* n4 = new TreeNode<Monster>(m4);
TreeNode<Monster>* n5 = new TreeNode<Monster>(m5);
TreeNode<Monster>* n6 = new TreeNode<Monster>(m6);
TreeNode<Monster>* n7 = new TreeNode<Monster>(m7);
m_pRoot = n5;
n5->pLeft = n4;
n5->pRight = n6;
n4->pLeft = n1;
n1->pRight = n2;
n6->pLeft = n3;
n3->pRight = n7;
size = 7;
}
template<class T>
TreeNode<T>* BSortTree<T>::GetRoot()
{
return m_pRoot;
}
template<class T>
int BSortTree<T>::GetDepth(TreeNode<T>* pNode)
{
if (pNode == NULL)
{
return 0;
}
else
{
int m = GetDepth(pNode->pLeft);
int n = GetDepth(pNode->pRight);
return (m > n) ? (m + 1) : (n + 1);
return 0;
}
}
template<class T>
void BSortTree<T>::InOrderTraverse(TreeNode<T>* pNode)
{
//中序遍历所有怪物,列出怪的名字
if (pNode == NULL)
{
return;
}
else
{
///左根右
InOrderTraverse(pNode->pLeft);
printf("%s", pNode->element.Name);
InOrderTraverse(pNode->pRight);
}
}
template<class T>
void BSortTree<T>::PreOrderTraverse(TreeNode<T>* pNode)
{
//前序遍历所有怪物,列出怪的名字
if (pNode == NULL)
{
return;
}
else
{
/// 循环遍历
printf("%s\n", pNode->element.Name);
PreOrderTraverse(pNode->pLeft);
PreOrderTraverse(pNode->pRight);
}
}
template<class T>
void BSortTree<T>::PostOrderTraverse(TreeNode<T>* pNode)
{
//后序遍历所有怪物,列出怪的名字
if (pNode == NULL)
{
return;
}
else
{
PostOrderTraverse(pNode->pLeft);
PostOrderTraverse(pNode->pRight);
printf("%s\n", pNode->element.Name);
}
}
void TestBinaryTree()
{
TreeNode<Monster>* m_pRoot = NULL;
TreeNode<Monster>* m_pRoot2 = NULL;
BSortTree<Monster> Bin;
m_pRoot = Bin.GetRoot();
Bin.GetDepth(m_pRoot);
printf("长度为%d:\n", Bin.GetDepth(m_pRoot));
//前序
Bin.PreOrderTraverse(m_pRoot);
//中
Bin.InOrderTraverse(m_pRoot);
//后
Bin.PostOrderTraverse(m_pRoot);
}
int main()
{
TestBinaryTree();
return 0;
}
1、有很好的查询性能
2、有很好的新增和删除的性能
3、若左子树不空,则左子树上所有结点的值均小于它的根结点的值
4、若右子树不空,则右子树上所有结点的值均大于它的根结点的值
5、左、右子树也分别为二叉排序树
搜索二叉树规则
以根开始 左小右大
二叉树的 新增 删除 查找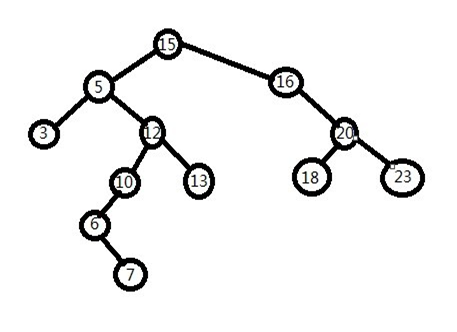
1、搜索二叉树的新增
例子 树45
45走右边 16 -20 -23-23右边
2、搜索二叉树的查找
例子 树13
小于根走左 比5大走右 比12大走13
3、搜索二叉树的删除
情况一:叶子节点
1、删除该节点
2、将父节点(左或者右)指针置NULL
情况2:只有一个子树
1、删除该节点
2、将父节点(左或者右)指针指向子树
情况3:左右子树都有
1、用右子树最小的节点取代源节点
2、再递归删除最小节点

这个双叉树代码不是我写的
#include<stdio.h>
#include<Windows.h>
#define SUCCESS 1 // 执行成功
#define ERROR -1 // 执行失败
template<class T>
class TreeNode {
public:
T element; //当前节点存储的数据
TreeNode<T>* pLeft; //指向左子节点的指针
TreeNode<T>* pRight; //指向右子节点的指针
TreeNode<T>* pParent; //指向父结点的指针
TreeNode(T& ele) {
//初始化Node节点
memset(&element, 0, sizeof(TreeNode));
//为元素赋值
memcpy(&element, &ele, sizeof(T));
pLeft = pRight = pParent = NULL;
}
//重载== 比较两结点是否相等
bool operator==(TreeNode<T>* node) {
return node->element == element ? true : false;
}
};
template<class T>
class BSortTree {
public:
BSortTree(); //构造函数
~BSortTree(); //析构函数
public: //判断树是否为空
bool IsEmpty(); //新增节点
DWORD Insert(T element); //删除节点
DWORD Delete(T element);
TreeNode<T>* Search(T element); //查找节点
void InOrderTraverse(TreeNode<T>* pNode); //中序遍历
void PreOrderTraverse(TreeNode<T>* pNode); //前序遍历
void PostOrderTraverse(TreeNode<T>* pNode); //后序遍历
private:
TreeNode<T>* GetMaxNode(TreeNode<T>* pNode); //获取以pNode为根的最大节点
TreeNode<T>* GetMinNode(TreeNode<T>* pNode); //获取以pNode为根的最小节点
TreeNode<T>* SearchNode(TreeNode<T>* pNode, T element); //
DWORD InsertNode(T element, TreeNode<T>* pNode); //新增节点
DWORD DeleteNode(T element, TreeNode<T>* pNode); //删除节点
void Clear(TreeNode<T>* pNode); //清空所有节点
private:
TreeNode<T>* m_pRoot; //根结点指针
int size; //树中元素总个数
};
template<class T>
BSortTree<T>::BSortTree()
{
m_pRoot = NULL;
size = 0;
}
template<class T>
BSortTree<T>::~BSortTree() {
Clear(m_pRoot);
}
template<class T>
DWORD BSortTree<T>::Insert(T element)
{
//如果根节点为空
if (!m_pRoot)
{
m_pRoot = new TreeNode<T>(element);
size++;
return SUCCESS;
}
//如果根节点不为空
return InsertNode(element, m_pRoot);
}
template<class T>
DWORD BSortTree<T>::InsertNode(T element, TreeNode<T>* pNode)
{
//将元素封装到节点中
TreeNode<T>* pNewNode = new TreeNode<T>(element);
//如果element == 当前节点 直接返回
if (element == pNode->element)
{
return SUCCESS;
}
//如果pNode的左子节点为NULL 并且element < 当前节点
if (pNode->pLeft == NULL && element < pNode->element)
{
pNode->pLeft = pNewNode;
pNewNode->pParent = pNode;
size++;
return SUCCESS;
}
//如果pNode的右子节点为NULL 并且element > 当前节点
if (pNode->pRight == NULL && element > pNode->element) {
pNode->pRight = pNewNode;
pNewNode->pParent = pNode;
size++;
return SUCCESS;
}
//如果element<当前节点 且当前节点的左子树不为空
if (element < pNode->element)
{
InsertNode(element, pNode->pLeft);
}
else
{
InsertNode(element, pNode->pRight);
}
return SUCCESS;
}
template<class T>
void BSortTree<T>::Clear(TreeNode<T>* pNode)
{
if (pNode != NULL)
{
Clear(pNode->pLeft);
Clear(pNode->pRight);
delete pNode;
pNode = NULL;
}
}
template<class T>
void BSortTree<T>::InOrderTraverse(TreeNode<T>* pNode)
{
if (pNode == NULL)
{
return;
}
else
{
InOrderTraverse(pNode->pLeft);
printf("%d\n", pNode->element);
InOrderTraverse(pNode->pRight);
}
}
template<class T>
void BSortTree<T>::PreOrderTraverse(TreeNode<T>* pNode)
{
if (pNode == NULL)
{
return;
}
else
{
printf("%d\n", pNode->element);
PreOrderTraverse(pNode->pLeft);
PreOrderTraverse(pNode->pRight);
}
}
template<class T>
void BSortTree<T>::PostOrderTraverse(TreeNode<T>* pNode)
{
if (pNode == NULL)
{
return;
}
else
{
PostOrderTraverse(pNode->pLeft);
PostOrderTraverse(pNode->pRight);
printf("%d\n", pNode->element);
}
}
template<class T>
bool BSortTree<T>::IsEmpty()
{
return size == 0 ? true : false;
}
template<class T>
TreeNode<T>* BSortTree<T>::GetMaxNode(TreeNode<T>* pNode)
{
if (pNode == NULL)
{
return NULL;
}
else
{
if (pNode->pRight == NULL)
{
return pNode;
}
else
{
GetMaxNode(pNode->pRight);
}
}
}
template<class T>
TreeNode<T>* BSortTree<T>::GetMinNode(TreeNode<T>* pNode)
{
if (pNode == NULL)
{
return NULL;
}
else
{
if (pNode->pLeft == NULL)
{
return pNode;
}
else
{
GetMinNode(pNode->pLeft);
}
}
}
template<class T>
TreeNode<T>* BSortTree<T>::Search(T element)
{
return SearchNode(m_pRoot, element);
}
template<class T>
TreeNode<T>* BSortTree<T>::SearchNode(TreeNode<T>* pNode, T element)
{
if (pNode == NULL) //如果节点为NULL
{
return NULL;
}
else if (element == pNode->element) //如果相等
{
return pNode;
} //如果比节点的元素小 向左找
else if (element < pNode->element)
{
return SearchNode(pNode->pLeft, element);
}
else //如果比节点的元素大 向右找
{
return SearchNode(pNode->pRight, element);
}
}
template<class T>
DWORD BSortTree<T>::Delete(T element)
{
if (!m_pRoot)
{
return ERROR;
}
//如果根节点不为空
DeleteNode(element, m_pRoot);
}
template<class T>
DWORD BSortTree<T>::DeleteNode(T element, TreeNode<T>* pNode)
{
if (pNode->pLeft == NULL && pNode->pRight == NULL && element != pNode->element)
{
printf("Can't find this element %d.\n", element);
return ERROR;
}
//叶子节点
if (pNode->pLeft == NULL && pNode->pRight == NULL && element == pNode->element)
{
TreeNode<T>* pParentNode = pNode->pParent;
if (pParentNode == NULL)
{
delete pNode;
pNode = NULL;
size--;
return SUCCESS;
}
else
{
int cmp = pParentNode->element > pNode->element ? 1 : 0;
switch (cmp)
{
case 1:
{
pParentNode->pLeft = NULL;
delete pNode;
pNode = NULL;
size--;
return SUCCESS;
}
case 0:
{
pParentNode->pRight = NULL;
size--;
delete pNode;
pNode = NULL;
return SUCCESS;
}
}
}
}
//一个子树
//左子树
if (pNode->pLeft != NULL && pNode->pRight == NULL && element == pNode->element)
{
TreeNode<T>* pReplaceNode = pNode->pLeft;
TreeNode<T>* pParentNode = pNode->pParent;
if (pParentNode == NULL)
{
m_pRoot = pReplaceNode;
m_pRoot->pParent = NULL;
delete pNode;
pNode == NULL;
size--;
return SUCCESS;
}
else
{
int cmp = pParentNode->element > pNode->element ? 1 : 0;
switch (cmp)
{
case 1:
{
pParentNode->pLeft = pReplaceNode;
pReplaceNode->pParent = pParentNode;
delete pNode;
pNode = NULL;
size--;
return SUCCESS;
}
case 0:
{
pParentNode->pRight = pReplaceNode;
pReplaceNode->pParent = pParentNode;
delete pNode;
pNode = NULL;
size--;
return SUCCESS;
}
}
}
}
//右子树
if (pNode->pRight != NULL && pNode->pLeft == NULL && element == pNode->element)
{
TreeNode<T>* pReplaceNode = pNode->pRight;
TreeNode<T>* pParentNode = pNode->pParent;
if (pParentNode == NULL)
{
m_pRoot = pReplaceNode;
m_pRoot->pParent = NULL;
delete pNode;
pNode == NULL;
size--;
return SUCCESS;
}
else
{
int cmp = pParentNode->element > pNode->element ? 1 : 0;
switch (cmp)
{
case 1:
{
pParentNode->pLeft = pReplaceNode;
pReplaceNode->pParent = pParentNode;
delete pNode;
pNode = NULL;
size--;
return SUCCESS;
}
case 0:
{
pParentNode->pRight = pReplaceNode;
pReplaceNode->pParent = pParentNode;
delete pNode;
pNode = NULL;
size--;
return SUCCESS;
}
}
}
}
//有左右子树
if (pNode->pLeft != NULL && pNode->pRight != NULL && element == pNode->element)
{
TreeNode<T>* pReplaceNode = GetMinNode(pNode->pRight);
TreeNode<T>* pParentNode = pNode->pParent;
//换节点的数据
memcpy(&pNode->element, &pReplaceNode->element, sizeof(T));
//删除右子树最小节点
DeleteNode(pNode->element, pNode->pRight);
return SUCCESS;
}
if (element > pNode->element)
{
DeleteNode(element, pNode->pRight);
return SUCCESS;
}
if (element < pNode->element)
{
DeleteNode(element, pNode->pLeft);
return SUCCESS;
}
}
void TestSerch()
{
//12 8 5 9 17 15 13
/*
12
8 17
5 9 15
13
*/
BSortTree<int> tree;
tree.Insert(12);
tree.Insert(8);
tree.Insert(5);
tree.Insert(9);
tree.Insert(17);
tree.Insert(15);
tree.Insert(13);
//删除左右
tree.Delete(8);
//删除根
tree.Delete(12);
//删除只有左子树
tree.Delete(9);
//删除叶节点
tree.Delete(5);
TreeNode<int>* p = tree.Search(17);
printf("%x %d\n", p, p->element);
}
int main()
{
TestSerch();
return 0;
}
完结 以上代码借鉴了部分人的代码,再次感谢
本文来自博客园,作者:逆向狗,转载请注明原文链接:https://www.cnblogs.com/Agtw/p/17117328.html




 浙公网安备 33010602011771号
浙公网安备 33010602011771号