CF1648D Serious Business 题解

前言

关于此题，CF 的官方题解是利用线段树优化 DP，但在赛后，hehezhou 提出过一种利用 cdq 分治优化 DP 的解法，然后蒟蒻便在神仙 \(\color{balck}{\text B} \color {red}{\text {indir0}}\) 的帮助下成功用 cdq 分治通过了本题

题解

设 \(dp_i\) 表示从 \((1, 1)\) 到 \((2, i)\) 的最大权值，有转移：

\[dp_i = \max\limits_{j < i}\{dp_j + s_{2, i} - s_{2,j} - \text{cost}(i, j)\} \]

\(s_{i, j} = \sum_{k\le j} a_{i,k}\)，\(\text{cost}(i, j)\) 表示同时包含 \((2,i), (2, j)\) 的花费最小的一个 offer

初始值：

\[dp_i = s_{1,i} + a_{2, i} - \text{cost}(i, i) \]

那个 \(\max\limits_{j \le i}\) 很烦，要 \(O(n^2)\) 做，直接 cdq 分治变为 \(O(n\log n)\)

在来看如何快速地求 \(\text{cost}(i, j)\)

在 cdq 分治时，设当前分治范围为 \([L, R]\)，中点为 \(mid\)，我们可以考虑将跨过 \(mid\) 的 offer 存下来用来转移

设 offer 的覆盖范围为 \([l, r]\)，花费为 \(w\)，我们便可以把 \(\text{cost}(i, j)\) 视作 \(w\)， 试着将 \(i \in [l,mid]\) 的 \(dp_i\) 转移给 \(j \in (mid, r]\) 的 \(dp_j\)，但这个暴力转移时间复杂度显然是不对的

转化 DP 式子：

\[\begin{aligned} dp_i &= \max\limits_{j < i}\{dp_j + s_{2, i} - s_{2,j} - w\}\\ &= \max\limits_{j < i}\{dp_j - s_{2, j}\} + s_{2, i} - w \end{aligned} \]

所以将跨中点的 offer 按右端点降序排序，维护 \([L, mid]\) 的后缀最大值，双指针转移即可

暴力找跨中点的 offer 时，如果当前 offer 涉及了左区间，就传给左儿子 \([L, mid]\)，右儿子同理，这样就能保证扫到的 offer 不会在范围外，优化一点时间

但是这样会被卡，考虑 offer 的范围都是 \([1, n]\)， 那么每个 offer 就会被扫到 \(4n\) 次，直接 T 飞

其实在分治时，可以多维护一个 \(mn\)，表示包含当前区间所有 offer 的最小花费

显然这个 \(mn\) 可以更新跨当前 \(mid\) 的任何转移，并且可以遍历 offer 时，用包含儿子的 offer 的花费来更新 \(mn\) 以递归，同时这些包含儿子的 offer 也不用传递给儿子了

这样可以保证每个 offer 只会被扫到 \(O(2 \log n)\) 次，可以接受

至此，总时间复杂度 \(O(n\log^2n)\)

细节

I. 如果给一个 \(dp_i\) 赋初值所用的 offer 的花费，再一次被用来将 \(dp_i\) 转移给其他的 \(dp_j\)，那么就会算重

比如下面这张图：

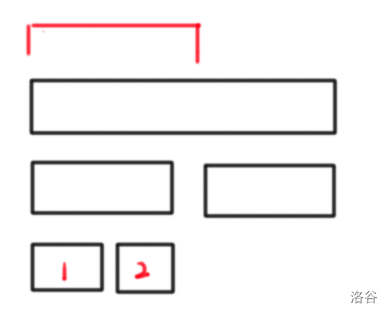
黑色的是 cdq 分治区间，红色的是一个花费为 \(w\) 的 offer ，\(1, 2\) 是两个分治区间的叶子，那么我给 \(dp_1\) 赋初的初值是 \(a_{1,1} + a_{2, 1} - w\)

此时我要利用 \(dp_1\) 来转移 \(dp_2\)，由于这个 offer 是同时包含了 \(1, 2\) 的，所以我可以让 \(dp_2 = max\{dp_2, dp_1 + a_{2, 2} - w\}\)，而此时 \(w\) 就被减了两次，出锅了

我们只需再转移时多取一个 \(\max\)，即

\[dp_i = \max\limits_{j < i}\{dp_j + s_{2, i} - s_{2,j} - w, s_{1, j} + s_{2, i} - s_{2, j - 1} - w\} \]

相当于把进入 \((2, i)\) 和 \((2, j)\) 的费用一起考虑了

所以再维护后缀最大值时要维护两种情况的

II. 发现一个左端点为 \(mid + 1\) 的 offer 也可以用来转移！

因为 \(dp_{mid}\) 表示的是到 \((2, mid)\) 的最大权值，所以我还可通过这个 offer 将 \(dp_{mid}\) 转移给右儿子，因此对于一个 \([l, r]\) 的 offer，实际可转移的范围为 \([l - 1, r]\)，前提是用 \(dp_{l - 1}\) 来转移，而不能用 \(s_{1, l - 1}\)（必须保证在 \((2, l - 1)\) 这个点）

III. 注意将 \(dp\) 初始化为 \(-\infty\) 时，不要赋得太小，导致爆 long long 炸成 \(+\infty\)

代码

#include <bits/stdc++.h>
using namespace std;
#define re register
#define ll long long
const int N = 5e5 + 5;
const ll inf = 1e17;
int n, m;
ll s[4][N];
struct node
{
    int l, r;
    ll w;
}a[N];
ll dp[N], mx[2][N];
vector<int> v[N << 2];
inline bool cmp(const int &x, const int &y) {return a[x].r > a[y].r;}
inline void cdq(int p, int l, int r, ll mn)
{
    if (l == r) return dp[l] = max(dp[l], s[1][l] + s[2][l] - s[2][l - 1] - mn), void();
    int mid = l + r >> 1;
    vector<int> link;
    ll lmn = mn, rmn = mn;
    for (auto i : v[p])
    {
        if (a[i].l <= l && a[i].r >= mid) lmn = min(lmn, a[i].w);
        else if (a[i].l <= mid) v[p << 1].push_back(i);
        if (a[i].l <= mid + 1 && a[i].r >= r) rmn = min(rmn, a[i].w);
        else if (a[i].r > mid) v[p << 1 | 1].push_back(i);
        if (a[i].l - 1 <= mid && a[i].r > mid) link.push_back(i);
    }
    cdq(p << 1, l, mid, lmn);
    mx[0][mid + 1] = mx[1][mid + 1] = -inf;
    int L = max(l - 1, 1);
    for (re int i = mid; i >= L; --i)
        mx[0][i] = max(mx[0][i + 1], s[1][i] - s[2][i - 1]),
        mx[1][i] = max(mx[1][i + 1], dp[i] - s[2][i]);
    sort(link.begin(), link.end(), cmp);
    auto now = link.begin();
    ll MX = max(mx[0][l], mx[1][L]) - mn;
    for (re int i = r; i > mid; --i)
    {
        while (now != link.end() && a[*now].r >= i)
        {
            MX = max(MX, max(mx[0][max(a[*now].l, l)], mx[1][max(a[*now].l - 1, L)]) - a[*now].w);
            ++now;
        }
        dp[i] = max(dp[i], MX + s[2][i]);
    }
    cdq(p << 1 | 1, mid + 1, r, rmn);
}
signed main()
{
    n = read(), m = read();
    for (re int i = 1; i <= 3; ++i)
        for (re int j = 1; j <= n; ++j) s[i][j] = s[i][j - 1] + read();
    for (re int i = 1; i <= m; ++i) a[i] = {read(), read(), read()};
    ll mn = inf;
    for (re int i = 1; i <= m; ++i)
    {
        if (a[i].l <= 1 && a[i].r >= n) mn = min(mn, a[i].w);
        else v[1].push_back(i);
    }
    for (re int i = 1; i <= n; ++i) dp[i] = -inf;
    cdq(1, 1, n, mn);
    ll ans = -inf;
    for (re int i = 1; i <= n; ++i)
    {
        ll val = dp[i] + s[3][n] - s[3][i - 1];
        ans = max(ans, val);
    }
    printf("%lld", ans);
    return 0;
}