Query on a tree 系列之树剖解法
\(\texttt{Qtree}\) 系列树剖题解(告别 \(\texttt{LCT}\) !)
前言
众所周知 Qtree 系列是 LCT 的题目
但由于蒟蒻平衡树写的fhq,不会Splay,所以蒟蒻不会 LCT,所以蒟蒻决定用树剖写完 Qtree 系列的所有题
QTREE - Query on a tree
直接树剖加线段树,每个点的权值为指向父亲的边权。
注意不要把 LCA 算进去了
Luogu 的 vjudge 只能用 C语言 ,害得我 CE 了一页
关于本题 C 语言的 \(\texttt{Tips}\) :
- 不要用
inline - 头文件选择
#include <ctype.h>和
#include <stdio.h>就够了 - 不要快读,只能用
scanf和printf - 没有
max和swap函数,要自己手写 - 没有
const - 不能
using namespace std; - 没有
string类型 - 函数间不能用
,,比如不能写dfs(1), dfs(2);,只能写dfs(1); dfs(2);
希望你能少 CE 一点
QTREE2 - Query on a tree II
路径和可以树上前缀和
求第 \(k\) 个点时先判和 LCA 的关系,如果大于 \(dep_u - dep_{lca}\) ,就找 \(v\) 的 \(len - k\) 级祖先,否则找 \(u\) 的 \(k - 1\) 级祖先
LCA 用重剖,\(k\) 级祖先用长剖,总时间 \(O(nlogn)\)
长剖写错,多测不清空会 RE!!!
QTREE3 - Query on a tree III
线段树维护区间最浅点,查询向上跳就行了
最简单的一题
(要不是 Qtree1 只能写 C语言)
QTREE4 - Query on a tree IV
难度陡然上升
先树剖,并对每条重链开一棵线段树
对于线段树上的一个节点 \(p\),其对应区间为 \([L,R]\)(重链上的一条路径)
记 \(lmx_p\) 表示从 \(L\) 出发,在 \([L,R]\) 间的某个节点拐出重链能到达的最远白点,\(rmx_p\) 同理,\(mx_p\) 表示 LCA 在\([L,R]\) 间的每对白点间距离的最大值
考虑线段树合并
记当前线段树上节点为 \(p\),区间为 \([L,R]\) ,左右儿子分别为 \(ls\) 对应\([L,mid]\),\(rs\) 对应 \([mid+1,R]\)
\(lmx_p=\max\{lmx_{ls},dis(L,mid+1)+lmx_{rs}\}\)
\(rmx_p=\max\{rmx_{rs},dis(mid,R)+rmx_{ls}\}\)
\(mx_p=\max\{mx_{ls},mx_{rs},rmx_{ls}+dis(mid,mid+1)+lmx_{rs}\}\)
接下来考虑边界(线段树叶子节点)
记当前线段树上节点为 \(p\),对应 \([L,L]\)
记 \(d_i, d’_i\) 表示以 \(i\) 为根的轻子树内,根到白点的最远距离和次远距离,不存在即为 \(-\infty\)
当 \(L\) 为白点时:
\(lmx_p=rmx_p=\max\{0,d_L\}\)
\(mx_p=\max\{0,d_L,d_L+d'_L\}\)
当 \(L\) 为黑点时:
\(lmx_p=rmx_p=d_L\)
\(mx_p=d_L+d'_L\)
\(d\) 和 \(d’\) 如何维护?
记当前节点为 \(u\) ,它的一个轻儿子为 \(v\)
由于 \(u\) 在重链上,\(v\) 是 \(u\) 的轻儿子,所以 \(v\) 一定是另一条重链的开端
所以 \(v\) 的 dfn 就是 \(v\) 所在的这条重链所对应区间的左端点
所以从 \(v\) 出发到其子树内最远白点的距离就是这条重链的线段树的根的 \(lmx\)
记这个根为 \(p\)
若 \(u\) 为白点:\(d_u=\max\{w(u,v)+lmx_p,0\}\)
若 \(u\) 为黑点:\(d_u=\max\{w(u,v)+lmx_p\}\)
具体可以每个节点开一个 multiset,把轻儿子的 \(lmx+w\)丢进去,如果是白点再丢个 \(0\) ,那么 \(d\) 就是堆顶
对于修改,只需不断向上跳重链,同时删除原来贡献,加入新的贡献
由于一次修改最多更新 \(logn\) 次,所以时间复杂度为 \(O(nlog^2 n)\)
这样写属实有点搞心态,而且三个 \(log\) 有点丑
还有个比较简便的做法
可以添加虚点将树变为二叉树,如图
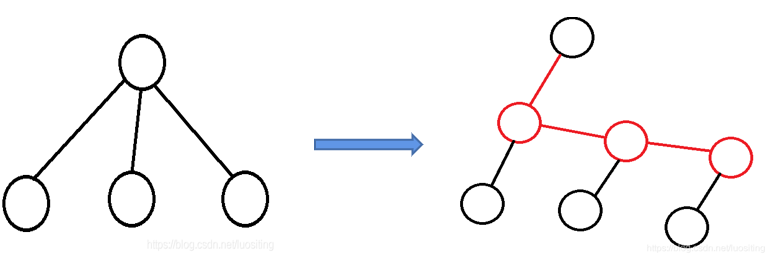
红点为虚点,红边边权为 \(0\)
这样每个点只有一个重儿子,一个轻儿子,那么 \(d\) 就唯一确定,\(d'\) 必为 \(-\infty\) ,不需要开 multiset 了
QTREE5 - Query on a tree V
树剖解法
网上没找到写树剖的题解,蒟蒻试着写了一下树剖,其表现良好,写篇题解为像我一样不会 LCT 的同学提供一种思路
虽然树剖比 LCT 多一个 log,但凭借优秀的常数跑得还是比大部分 lct 更快 (目前排 luogu 最优解第四)
与 Qtree4 类似,每条重链开一棵线段树
对于线段树上的一个节点 \(p\),其对应区间为 \([L,R]\)(重链上的一条路径)
记 \(lmn_p\) 表示从 \(L\) 出发,在 \([L,R]\) 间的某个节点拐出重链能到达的最近白点(这点与 Qtree4 不同),\(rmn_p\) 同理。(由于询问是关于某个点的信息,不再是全局信息了,所以不需要维护 \(mx\))
转移与 Qtree4 类似
\(lmn_p = \min\{lmn_{ls},dis(L,mid+1)+lmn_{rs}\}\)
\(rmn_p = \min\{rmn_{rs},dis(mid, R)+rmn_{ls}\}\)
记 \(d_i\) 表示以 \(i\) 为根的轻子树内,根到白点的最远距离,不存在为 \(+\infty\) (这点不同)
这里同样改建二叉树以维护 \(d_i\) ,\(v\) 是 \(u\) 的轻儿子
若 \(u\) 为白点:\(d_u=\min\{w(u,v)+lmn_p,0\} = 0\)
若 \(u\) 为黑点:\(d_u=w(u,v)+lmn_p\)
线段树边界节点 \(p\),对应区间 \([L, L]\):
当 \(L\) 为白点时:
\(lmn_p=rmn_p=\min\{0,d_L\} = 0\)
当 \(L\) 为黑点时:
\(lmx_p=rmx_p=d_L\)
以上部分与 Qtree4 的解题思路相仿,略微改动就行,更新颜色也和 Qtree4 一样,不断跳链即可
重点是如何根据我们维护的 \(lmn\) 和 \(rmn\) 得到距 \(u\) 最近白点 \(v\) 的 \(dis(u, v)\)
由于我们维护的是以左端或右端为起点的最小距白点距离,所以只有当 \(u\) 为区间的边界时,我们才能直接用上对应的 \(lmn\) 和 \(rmn\)
所以设当前询问点 \(u\) 所在重链的 \(\text{dfn}\) 区间为 \([L,R]\)
那么 \(u\) 在这条重链上的答案(指白点在以链顶为根的子树内)可由以下两种情况贡献:
-
\(u\) 作为左端点,贡献 \(lmn\),即 \(lmn_{[dfn_u,R]}\),相当于统计链底到 \(u\) 的答案
-
\(u\) 作为右端点,贡献 \(rmn\),即 \(rmn_{[L,dfn_u]}\),相当于统计 \(u\) 到链顶的答案
这条重链的答案为上述两种情况取 \(\min\)
而对于白点在子树外的情况,只需不断跳重链,跳到根为止,统计新的重链的答案,跳的时候加上链顶到 \(u\) 的距离,最后再对条重链上的答案取个最小值便是此次询问的答案
由于跳 \(O(logn)\) 条重链,每条重链统计答案需要 \(O(logn)\) 的时间,所以总时间复杂度 \(O(nlog^2n)\)
注意的是这道题所有节点初始为黑色
QTREE6 - Query on a tree VI
这题树剖有两种解法,一种是延续 IV、V 的思路,维护端点最值,另一种是每个点单独考虑,这边先写的第二种,第一种后面补
设 \(b_u, w_u\) 分别表示在以 \(u\) 为根的子树内,如果 \(u\) 为 黑/白 点,\(u\) 的同色最大联通块的大小
初始由于全是黑点,所以 \(b_u = siz_u, w_u = 1\)
询问时,只需向上跳到最远的与 \(u\) 同色的点,它的 \(b\) /\(w\) 即为答案
对于修改,先考虑把 \(u\) 由黑变白
-
由于 \(u\) 不再是黑点了,所以有它是黑点所带来的贡献要全部删去。
而 \(u\) 所贡献的只能是它的祖先,并且与它在同一个黑色连通块内,或者是在 \(u \rightarrow root\) 路径上第一个白点(贡献这个白点为黑点时的答案),所以找到第一个白点 \(v\),\(fa_u \rightarrow v\) 路径上所有点的 \(b\) 减去 \(b_u\) (相当于 \(u\) 阻断了祖先的黑色连通块与子树内的黑色连通块)
-
由于 \(u\) 变为了白点,所以它会带来一些贡献
而 \(u\) 所贡献的也是它的祖先,并与它在同一个白色联通块内,或者是在 \(u \rightarrow root\) 路径上第一个黑点,所以找到第一个黑点 \(v\),\(fa_u \rightarrow v\) 路径上所有点的 \(b\) 加上去 \(w_u\) (相当于 \(u\) 联通了祖先的白色连通块和子树内的白色联通块)
这两步都可以用线段树区间加实现
还有个问题就是怎么求 \(u \rightarrow root\) 路径上的第一个 ,这个与 Qtree3 类似
而至于求 \(u \rightarrow root\) 上最远的同色连通块内的点,Qtree3 的操作改一下就行了,即每次查父亲到父亲链顶的第一个异色点,没查到就跳到父亲链顶的位置,否则特判:如果这个异色点是父亲,就返回当前点;否则返回这个点的重儿子。具体看代码
细节比较多,但只要熟悉树剖都能发现
码量和常数似乎都变大了
QTREE7 - Query on a tree VII
还是利用 QTree4 的思想
线段树合并:当前节点 \(p\) ,表示区间为 \([L,R]\)
设 \(lmx_{p}\) 表示 \(L\) 所在同色连通块内的最大权值
设 \(rmn_{p}\) 表示 \(R\) 所在同色连通块内的最大权值
光这样显然是合并不了的,考虑合并需要什么
对于当前节点 \(p[L,R]\) ,左右儿子分别为 \(ls[L,mid]\),\(rs[mid + 1, R]\)
显然 \(lmx_{ls}\) 可以贡献给 \(lmx_p\) ,但 \(lmx_{rs}\) 呢?
如果左儿子全是一个颜色,并且与右儿子最左边的颜色相同,那么是不是 \(lmx_{rs}\) 也可以贡献给 \(lmx_p\)?
所以设 \(lsiz_p\) 表示左端点所在同色连通块包含区间内的点数(即 \(L\) 在重链上的同色连通块的大小),\(rsiz_p\) 同理
那么转移就出来了:
\(lmx_p = \max(lmx_{ls} , lmx_{rs}[lsiz_{ls} = mid - l + 1][col_{mid} = col_{mid +1}])\)
\(rmx_p = \max(rmx_{rs} , rmx_{ls}[rsiz_{rs} = r - mid][col_{mid} = col_{mid+}])\)
\(lsiz_p = lsiz_{ls} + lsiz_{rs}[lsiz_{ls} = mid - l + 1][col_{mid} = col_{mid +1}]\)
\(rsiz_p = rsiz_{rs} + rsiz_{ls}[rsiz_{rs} = r - mid][col_{mid} = col_{mid +1}]\)
边界情况:设 \(v\) 为 \(u\) 的轻儿子
\(lmx_u = rmx_u = \max\limits_v \{lmx_{rt_v}[col_u = col_v], w_u\}\)
\(lsiz_u = rsiz_u = 1\)
询问:
只需跳到最浅的,同一同色连通块内的祖先,再查,该祖先到其所在链链底这个区间, \(lmx\) 即为答案,但要注意特判跳到根的情况,以及跳时颜色是否相同,细节看代码
修改:
先删除原来的贡献,加入新的贡献,这个只需每个点每个颜色用一个 multiset 维护,记录该颜色连通块内的最大权值即可
然后一边跳重链一边改,同时记录上一个节点(从哪里跳来),和之前的贡献,以便删除贡献和添加贡献,细节在于改颜色时上一个点是否就是修改的点,如果是,在删贡献是要在反色 multiset 里面删(它原来的贡献是存在那里面的)
也是调了好久,拍了一下午
好在树剖依旧稳定输出,拿下最优解第四


 该文章不被密码保护
该文章不被密码保护



 浙公网安备 33010602011771号
浙公网安备 33010602011771号