差分约束系统与图论的联系（最短路SPFA算法）

@

目录

• 差分约束系统
  • 1.何为差分约束系统？
  • 2.差分约束系统求解
  • 3.差分约束系统与最短路
  • 4.与有向图结合的例子
• 最短路算法SPFA
  • 1.引入SPFA的意义
  • 2.SPFA算法思想
  • 3.SPFA算法复杂度
  • 4.例子
• 应用

差分约束系统

1.何为差分约束系统？

如果一个系统由n个变量和m个约束条件组成，约束条件形如
\(x_i\) - \(x_j\) <= k(i,j∈[1,n])，则成为差分约束系统。
例如：
\(x_1\)-\(x_3\) <= 5
\(x_1\)-\(x_2\) <= 2
\(x_2\)-\(x_3\) <= 1

2.差分约束系统求解

以上式差分约束系统为例，若想求\(x_1\)到\(x_3\)的最小值，我们可以由第一个约束条件看出\(x_1\) - \(x_3\)的最大值是5，但通过把第二个与第三个不等式相加，我们可以得到：\(x_1\) - \(x_3\) <= 3，最后我们验证3才是最优解。
现在我们把约束条件\(x_i\) - \(x_j\) <= k移项，可得：\(x_i\) <= \(x_j\) + k，并设\(x_1\) = 0再模拟上述过程，我们发现，当且仅当\(x_i\) <= \(x_j\) + k时，\(x_i\)的值被改变成了\(x_j\) + k，学习过最短路径的hxd相信已经发现了其中的奥秘。
在SPFA，dijkstra等最短路算法中，当\(x_i\) <= \(x_j\) + k时，我们进行两点之间的松弛操作，即更新源点到点\(x_i\)的最短路径为\(x_j\) + k。

3.差分约束系统与最短路

差分约束系统的解法用到了单源最短路径问题中的三角形不等式。对有向图中的一条边<u,v>来说，都有\(dis[v]≤dis[u]+len[u][v]\)，其中\(dis[u]\)表示源点到u结点的最短路径，v结点同理。\(len[u][v]\)表示，u与v的边的长度。
三角不等式是显然的，从源点到顶点v的最短路径长度小于等于从源点到顶点 u的最短路径长度加上边 <u,v> 的长度值。

4.与有向图结合的例子

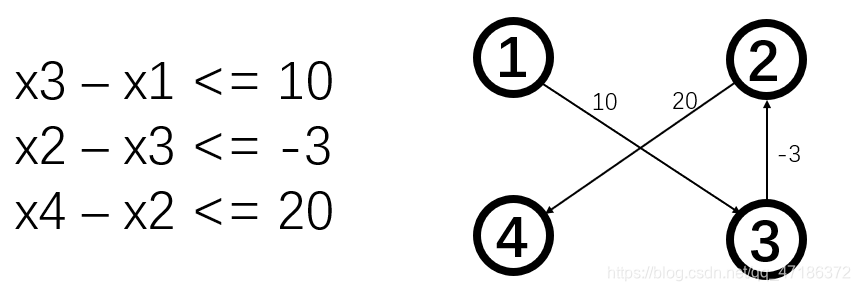
将左侧的不等式转化为有向图可得右图。若求解 \(x_1 - x_4\)的最大值只需求解顶点\(x_1\) 到顶点 \(x_4\)的最短路径即可。显然看出所求解为27，我们再将三个不等式相加，可以得到\(x_1 - x_4 <= 27\)，即验证了结论。

最短路算法SPFA

1.引入SPFA的意义

差分约束系统经常与最短路联系起来，与平时我们做的最短路不同的是。差分约束系统总是与带负权的最短路联系在一起，而dijkstra算法却没有办法解决带负权的最短路问题，这时SPFA就可以提供解决单源含负权最短路问题的思路，而且可以判断是否含有负环。

2.SPFA算法思想

SPFA与BFS的写法很类似，同样都需要一个队列。
①我们设数组d来表示最短路的值，\(d[u]\)表示源点到结点u的最短路径的长度。最开始，我们将源点s加入队列中，并设\(d[s] = 0\)，其他点设为INF。
②当队列不空时，我们进行循环，每次循环将队首元素取出，取出的结点设为u，并访问与u结点相连的所有结点，若存在边<u,v>且v结点不在队列中，我们就将v结点加入队列中，并对v结点做松弛操作。即如果\(d[v] > d[u]+<u,v>\)，就令\(d[v] = d[u] + <u,v>\)重复以上过程直至循环结束（即队列空）。
③SPFA算法结果：在循环过程中，如果一个结点进入队列的次数超过了结点个数N，则证明含有负环。若不存在负环，将\(d[u]\)输出就可以求得源点s到结点u的最短路的长度。

3.SPFA算法复杂度

SPFA的复杂度大约是O(kE),k是每个点的平均进队次数(一般的，k是一个常数，一般在1~2之间)。

4.例子

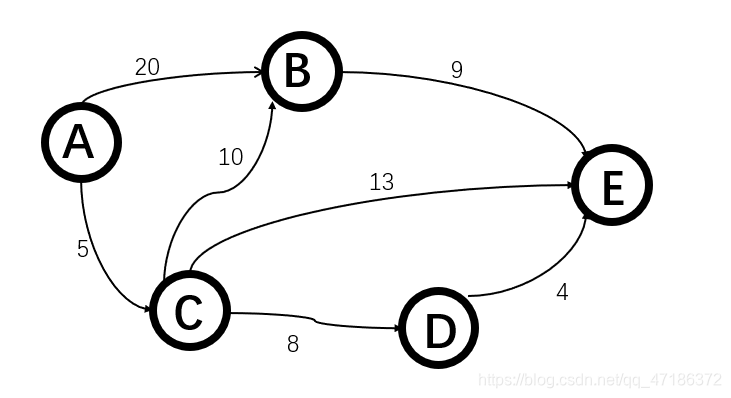
①我们设A为起点，初始化得
②与A相邻的结点有B、C，我们按算法的思想将dis与queue更新得：

③取出队首B，重复过程：

④一直循环，得如下分步：

应用

POJ3169.Layout 链接如下　　　
　　　　　　　　　　　快点我呀
思路：我们设d[i]为，第i头牛的位置，所以一定有\(d[i]<=d[i+1]\)，对于没对关系好的牛，有\(d[AL]+DL>=d[BL]\)，对于关系不好的牛，有\(d[AD]+DD<=d[BD]\)，讲上面三个不等式处理成差分约束系统可以得到：
　　　　　　　\(　d[i] <= d[i+1]+0\)
　　　　　　　\(d[BL] <= d[AL] + DL\)
　　　　　　　\(d[AD] <= d[BD] + (-DD)\)
所以我们在顶点i+1向顶点i连接一条权值为0的边，在AL到BL连接一条权值为DL的边，在BD到AD连接一条权值为-DD的边，由于存在负边，所以使用SPFA算法。
最后，如果存在负圈，则输出-1，如果\(d[N] = INF\)则1-N不可达，输出-2。
若可达且不存在负圈，则输出\(d[N]\)。
AC代码：

#include<iostream>
#include<cstdio>
#include<vector>
#include<queue>
#include<algorithm>

#define INF 0x7fffffff
using namespace std;

const int maxn = 1e3+5;
const int maxm = 1e4+5;
struct edge{
    int v,w;
    edge(int v1,int w1):v(v1),w(w1){};
};

int d[maxn],cnt[maxn];bool vis[maxn];
int n,ml,md;
vector<edge> G[maxn];
queue<int> q;

void solve(){
    fill(d+1,d+1+n,INF);
    fill(vis+1,vis+1+n,false);
    d[1] = 0;
    q.push(1);
    while(!q.empty()){
        int u = q.front();q.pop();
        vis[u] = false;
        for(int i = 0;i < G[u].size();i++){
            edge e = G[u][i];
            int v = e.v;
            int w = e.w;
            if(d[v] > d[u] + w){
                d[v] = d[u] + w;
                if(!vis[v]){
                    if(++cnt[v] > n){
                        printf("-1");
                        return;
                    }
                    q.push(v);
                    vis[v] = true;
                }
            }
        }
    }
    printf("%d",d[n] == INF ? -2 : d[n]);
}

int main(){
    int u,v,w;
    scanf("%d%d%d",&n,&ml,&md);
    for(int i = 0;i < ml;i++){
        scanf("%d%d%d",&u,&v,&w);
        G[u].push_back(edge(v,w));
    }
    for(int i = 0;i < md;i++){
        scanf("%d%d%d",&u,&v,&w);
        G[v].push_back(edge(u,-w));
    }
    for(int i = 1;i < n;i++){
        G[i+1].push_back(edge(i,0));
    }
    solve();
    system("pause");
    return 0;
}