2025-10-21 XQQ Round 赛后总结
赛时心路历程
- 开 T1,然后 think 一会就秒掉了。大洋里一遍过。
- 开 T2,然后 think 一会就秒掉了。大洋里也是一遍过。
- 15:48 think T3,结果假了。但是注意到在 \(m=0\) 的时候是对的,10 分也是分。
- 16:25 想不到 T3。注意到 T4 有很简单的 30pts 做法。决定过一会再写,先看 T3 能不能 think 出来。
- 17:02 放弃了。写 T4 性质吧。一个小时绝对够了。
- 17:28 解决了 T4 性质。开润。
T1 单调菜单
题意
有初始为空的可重集 \(S\),每次操作向其中添加一个数。问最多能从中选择多少个数,使选出的数中任意两个数之差均大于 \(1\)。
赛时
花了 0 分钟发现这题和我昨天炼石打到的一道维护连续段信息的题很像,所以就把这个做法搬过来了。
题解
很显然多个相等的数只能选一个,所以只需要维护集合里有没有某个数就行。
然后注意到两个连续段互不影响,同一个连续段至多选 \(\lceil\dfrac{size}{2}\rceil\) 个数。
所以用并查集维护连续段,合并连续段的时候提前减掉然后再加回来就行了。
肯定存在一些其他的做法,但我懒得想了。
时间复杂度 \(O(n\alpha(n))\)。
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define infll 0x3f3f3f3f3f3f3f3fll
using namespace std;
int n;
int a[300010];
bool tg[500010];
int fa[500010],siz[500010];
int find(int x){
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
void merge(int x,int y){
x=find(x);
y=find(y);
if(x==y) return;
if(siz[x]>siz[y]) swap(x,y);
fa[x]=y;
siz[y]+=siz[x];
}
int amax=0;
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
freopen("set.in","r",stdin);
freopen("set.out","w",stdout);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i],amax=max(amax,a[i]);
for(int i=1;i<=amax;i++) fa[i]=i,siz[i]=1;
int ans=0;
for(int i=1;i<=n;i++){
int x=a[i];
if(!tg[x]){
if(x!=1&&tg[x-1]) ans-=(siz[find(x-1)]+1)>>1,merge(x-1,x);
if(x!=amax&&tg[x+1]) ans-=(siz[find(x+1)]+1)>>1,merge(x+1,x);
tg[x]=1;
ans+=(siz[find(x)]+1)>>1;
}
cout<<ans<<" ";
}
cout<<"\n";
return 0;
}
T2 城市兜风
题意
给定一个 \(n\times m\) 的网格,其中 \(k\) 个位置存在障碍。初始在 \((1,1)\),每次移动可以朝任意方向移动任意距离,但不能越过障碍。
只能移动最多两次,问能到达的格子的总数。
赛时
盯出来了简单容斥。然后写了一坨东西,差点没给我自己绕晕。
题解
很显然,只能移动两次这个限制非常强。
考虑第一步向右走,那么这一步可以走到第一行中纵坐标最小的障碍物前。继续往下走,能走到的一定也是对应列中横坐标最小的障碍物前。
同理,也可以先往下走,再往右走。
通过预处理出每行的障碍物最小纵坐标、每列的障碍物最小横坐标,可以较为简单地求出上面两种情况各自的答案。
但是很显然,对于两种方法都能走到的格子会被计算两次。我们需要通过容斥减去这部分的贡献。
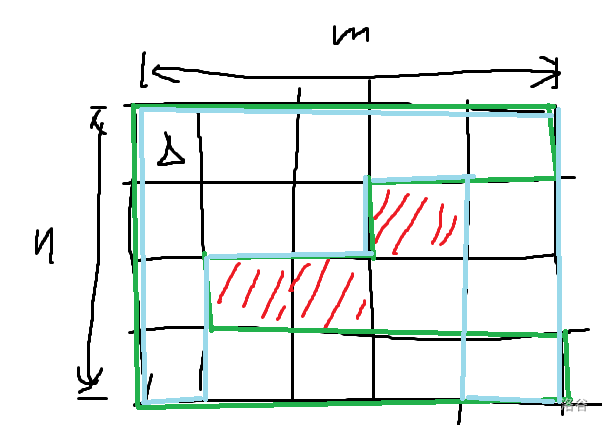
如上图:绿色部分是先向下再向右的答案,青色部分是先向右再向下的答案。我们要减去的就是两部分的交集。
我们把答案拆成每一行的绿色部分分别包含多少个青色部分,这些答案的和就是要求的交集。
而注意到青色部分有前缀性,所以我们只需要记录每一列的青色部分在哪一行结束就可以了。在找到对应行的时候把这一列的贡献消掉。
所以我们可以用树状数组非常方便地维护这个东西。
这大概也许算是个扫描线的思想吧。
因为写的有点石再加上这题细节本来就多,所以加了点注释。
时间复杂度 \(O(k+n\log m)\)。
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define infll 0x3f3f3f3f3f3f3f3fll
using namespace std;
int n,m,k;
// 存储点的坐标(但其实没什么意义)
struct node{
int x,y;
bool operator<(const node&_Q)const{return x==_Q.x?y<_Q.y:x<_Q.x;}
}a[200010];
// prerow - 对于每一列而言,能到达的纵坐标最大的格。
// precol - 对于每一行而言,能到达的横坐标最大的格。
int prerow[200010],precol[200010];
// 其实就是 precol[1] 和 prerow[1]。
int frowmin;
int fcolmin;
// 树状数组
int bit[200010];
static int lowbit(int x){return x&(-x);}
void add(int x,int v){
while(x<=m) bit[x]+=v,x+=lowbit(x);
}
int query(int x){
int res=0;
while(x) res+=bit[x],x-=lowbit(x);
return res;
}
// 青色部分结束的位置
vector<int> ops[200010];
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
freopen("motor.in","r",stdin);
freopen("motor.out","w",stdout);
cin>>n>>m>>k;
for(int i=1;i<=k;i++) cin>>a[i].x>>a[i].y;
for(int i=1;i<=n;i++) precol[i]=m;
for(int i=1;i<=m;i++) prerow[i]=n;
frowmin=m;
fcolmin=n;
for(int i=1;i<=k;i++){
precol[a[i].x]=min(precol[a[i].x],a[i].y-1);
prerow[a[i].y]=min(prerow[a[i].y],a[i].x-1);
if(a[i].x==1) frowmin=min(frowmin,a[i].y-1);
if(a[i].y==1) fcolmin=min(fcolmin,a[i].x-1);
}
// 统计前两类答案
long long ans1=0,ans2=0;
for(int i=1;i<=frowmin;i++) ans1+=prerow[i];
for(int i=1;i<=fcolmin;i++) ans2+=precol[i];
// 计算第三类答案
long long ans3=0;
// 预处理结束的行
for(int i=1;i<=frowmin;i++){
add(i,1);
if(prerow[i]!=n) ops[prerow[i]+1].push_back(i);
}
// 扫描线?
for(int i=1;i<=fcolmin;i++){
for(int x:ops[i]) add(x,-1);
ans3+=query(precol[i]);
}
cout<<ans1+ans2-ans3<<"\n";
return 0;
}
总结
T1 典型的签到。
T2 容斥想到那一步有点难度,但总体还好。
T3 和 T4 只打了部分分。不会写。
后来润去打 TB 了。
吃完饭回来最后一分钟猜对了 T3 结论直接 AK。
半个小时爆切三道题。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号