【翻译】HOG, Histogram of Oriented Gradients / 方向梯度直方图 介绍
本文翻译自 Histogram of Oriented Gradients"
在这篇文章中,我们将会学习 HOG (Histogram of Oriented Gradients,方向梯度直方图)特征描述子 的详细内容。
我们将学习 HOG 算法是如何实现的,以及在 OpenCv / MATLAB 或者其他工具里面如何计算特征子。
这篇文章是我正在写的,关于 Image Recognition / 图像识别 和 Object Detection / 目标检测 系列文章中的一部分。
很多事情看起来困难又神秘,但是你一旦花时间去了解,揭开神秘面纱,你就会发现神奇之处。
如果你是一个初学者,觉得计算机视觉又难又神秘,请记住一句话:
问:如何吃掉一个大象?
答:一口一口吃
什么是 Feature Desciptor / 特征描述子
Feature Desciptor / 特征描述子 从图像中提取有用信息,剔除无关信息;
典型的,特征描述子从将一张 宽度 * 高度 * 3 ( 通道数 ) 大小的图像,提取出长度为 n 的 Feature Vector / 特征向量 或者 Feature Array / 特征矩阵;
比如 HOG 特征描述子会从一张 64 * 128 * 3 的图像中提取出长度为 3780 的特征向量;
请记住, HOG 的特征描述子也可以计算其他尺寸,但是这篇文章中,我使用上述尺寸,以便你能够轻松的理解概念。
这些概念听起来都挺不错,但是哪些是“有用的信息”,有些又是“无用的信息"?
定义“有用的信息”,我们需要知道有用的信息用来干什么的;
很明显,通过特征向量用来浏览图像是没用的,但是在图像识别或者目标检测中,特征向量会变得很有用;
在一些图像分类算法中比如 SVM,Support Vector Machine,支持向量机 中,用特征向量进行分类会达到很好的结果。
但是在分类任务中,哪些特征是有用的呢?
我们借助下面的例子来讨论,比如现在我们想通过一个目标检测器,可以检测衬衫和大衣的纽扣;
一个纽扣是一个圆形(图片中也有可能看起来像是椭圆),一般来说有几个孔,用于缝到衣服上面;
你可以在纽扣的图像上使用一个 Edge detector / 边缘检测器,可以轻松通过检测边缘来辨别它是不是一个纽扣;
这个例子中,边缘信息是“有用的”而颜色信息是 ”无用的“;
除此之外,特征也需要有足够特殊的地方。比如一个好的特征,应该能够让你辨别出纽扣和其他圆形的物体,比如硬币和汽车轮胎。
如何计算 Histogram of Oriented Gradients / 方向梯度直方图?
在这一节,我们会继续深入学习如何计算 HOG 特征描述子。
步骤1:预加工
之前提到用于行人检测的 HOG 特征描述子,是基于 64×128 大小的图像。当然,图像可能是任何尺寸的;
对于这些之后用于分析的图像,唯一需要进行的处理是调整纵横比图像大小;
在我们的例子中,需要调整纵横比为1:2,比如图像可以被调整为 100×200, 128×256, 或者 1000×2000,但是不能是 101×205;
原始图像大小是 720×475,我们截切出来 100×200 大小图像用来计算 HOG 特征描述子,然后重新调整大小到 64×128;
现在我们就做完了计算 HOG 特征描述子准备工作。

Dalal 和 Triggs 的论文也提到了 Gamma Correction / 伽马校正 作为预处理步骤,但性能提升很小,因此我们选择预处理中跳过这一步。
步骤 2 :计算梯度图像
为了计算 HOG 特征描述子,我们第一步需要计算水平和垂直方向的梯度。我们通过下面的 Kernel / 核 来处理图像,很容易计算出梯度的直方图。

我们可以使用核大小为 1 的 OpenCv 的 Sobel 算子:
1 // C++ gradient calculation.
2 // Read image
3 Mat img = imread("bolt.png");
4 img.convertTo(img, CV_32F, 1/255.0);
5
6 // Calculate gradients gx, gy
7 Mat gx, gy;
8 Sobel(img, gx, CV_32F, 1, 0, 1);
9 Sobel(img, gy, CV_32F, 0, 1, 1);
1 # Python gradient calculation
2
3 # Read image
4 im = cv2.imread('bolt.png')
5 im = np.float32(im) / 255.0
6
7 # Calculate gradient
8 gx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)
9 gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)
接下来,我们通过下面的公式来计算梯度的幅值和方向:

在 OpenCv 中,我们可以使用 cartToPolar 函数来计算上述数值:
// C++ Calculate gradient magnitude and direction (in degrees)
Mat mag, angle;
cartToPolar(gx, gy, mag, angle, 1);
The same code in python looks like this.
# Python Calculate gradient magnitude and direction ( in degrees )
mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)
下图展示了梯度计算结果:

左边:x 方向梯度的绝对值
中间:y 方向梯度的绝对值
右边:梯度的幅值
注意 x 方向的梯度代表垂直方向的变化趋势,而 y 方向代表的是水平方向的变化;
如果图像像素变换迅速的话,可以在梯度图中明显看出,而当区域内变化缓慢时,不会出现梯度幅值;
梯度图像去除了很多不必要的信息,保留了关键信息。换句话说,你可以看着梯度图,然后轻松的辨别出来照片里的人;
每一个像素点,都有一个 Magnitude / 幅值 和 Direction / 方向;
对于彩色的图像,三种通道的梯度都会被评估计算,取的是最大的梯度。
步骤 3:在 8*8 cells / 网格 中计算梯度直方图
这一步,图像会被分割成 8*8 大小的单独 cells / 小格子,然后对于每个 8*8 的小格子,分别计算梯度直方图;
我们先来了解下为什么要把图像分割为 8*8 的小格子;
有一个重要的原因是使用特征描述子来描述一幅 image / 图像 的一个 patch / 子图像 的话,网格分割会提供了一个 compact / 紧凑 的表示方式;
一个 8*8 的子图像包含 8*8*3 = 192 个像素值。每个像素梯度有两个值( Magnitude / 幅值 和 Direction / 方向 ),所以每个子图像会有 8*8*2=128 个数值;
在这节结束之前,我们会看到这 128 个数值如何使用 9 位的数组来 存储在 9 位的直方图中。经过压缩处理之后的数据具有更好的 抗噪性。
但是为什么取得是 8*8 的子图像而不是 32*32? 这是根据我们所要检测的目标来决定的;
对于 HOG 行人检测, 从 64*128 的行人图像中提取出的 8*8 子图像,已经足够用来提取出有用的信息(比如脸部,头的顶部等等)
直方图有必要是 9 位的向量,与 0,20,40,60… 160 度对应;
让我们来看看在一个 8*8 的子图像中,梯度是什么样的:
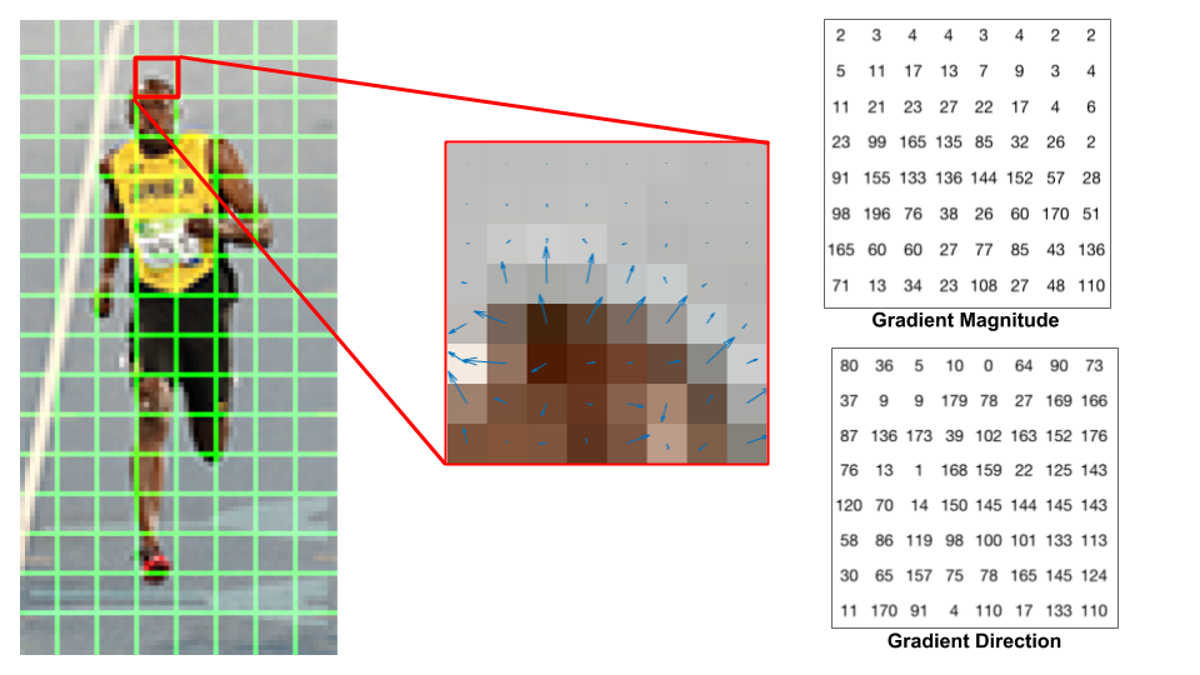
中间:用箭头来代表颜色和梯度的变化;
右边:用数字来代表子图像中的梯度;
如果你是一个计算机视觉的初学者,中间的图像会很有帮助很形象;
通过箭头来表示图像中梯度的变化,箭头的方向表示着像素强度变化的方向,幅值表示变化的缓慢;
通过右边的图,我们可以看到 8*8 子图像中提取出来的代表梯度的数值,这些角度从 0~180 度而不是 0~360 度,这些被称之为 unsigned gradients / 无符号梯度,因为一个梯度和它取负之后得到的是同样的数值;
换句话说,一个梯度箭头旋转180度之后被认为是一样的;
但是为什么我们不使用 0-360 度呢?经验告诉我们使用无符号的梯度,比使用有符号的梯度在行人检测中性能更好。不过一些 HOG 的实现中也可以允许你使用有符号的梯度。
接下来就是为这些 8*8 的子图像,建立一个梯度直方图。直方图有 9 位,来与 0, 20, 40…160 度相对应;
下面的图像向我们展示了操作过程,我们关注从 8*8 子图像中提取出来的幅值和方向;
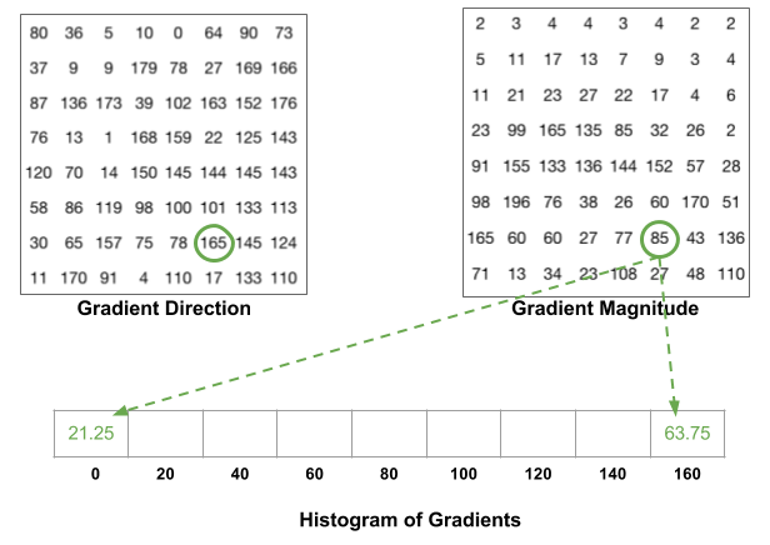
* 根据梯度的方向来选择使用填充到哪一位,然后根据梯度的幅值来填充数值;
我们先来看看 蓝圈的数值,角度为 80,幅值为2,所以在直方图第五位加 2;
再来看看 红圈的数值,角度为 10,幅值为 4,角度 10 的话在 0 和 20 之间,所以将它的幅值 4 被一分为 2 ,分别在直方图的 "0 位" 和 "20 位" 里面放 2 。

还需要注意的一点是,如果 角度比 160 大,在 160 和 180 之间。我们知道在这里 0 度和 180 度一样,所以下面这个例子,角度 165 度被分到了 0 度和 160 度 两个位里面。
8*8 子图像提取出来的数值,经过处理,可以得到一个 9 位的直方图,对于上面的子图像,我们可以得到如下的直方图:

在我们的表示中,y 轴默认为 0 度。你可以从直方图中看到,在 0~180 度之间有很多分布,这也表明子图像中的梯度方向要么朝上要么朝下。
步骤 4:16*16 块归一化
在之前的步骤中,我们根据图像的梯度制作了直方图。但是对于亮度不同的图像,梯度很敏感。
如果你让所有像素点的数值除 2 来让图像变暗,梯度幅值也会相应的减半,因此直方图也会对应着减半。
理想情况下,我们希望我们的描述器是不随着亮度变化而变化的,换句话说,我们想要归一化直方图,所以让它不受亮度影响;

在我说明直方图如何被归一化之前,让我们来看看,一个长度为 3 的向量是如何被归一化的;
比如我们有个 RGB 颜色向量为 [ 128, 64, 32 ],计算出长度为:
这也被称为这个向量的 L2 范数;
对向量的每个元素除以 146.64,得到归一化之后的向量 [ 0.87, 0.43, 0.22 ]。
现在考虑另一个向量,它的数值是之前向量的两倍,2 x [ 128, 64, 32 ] = [ 256, 128, 64 ];
通过同样的计算方式,你可以得到同样的归一化向量 [ 0.87, 0.43, 0.22 ],这就可以解决之前提到的亮度的影响问题。
现在我们知道了如何去归一化向量,也许你会认为,归一化 9*1 的直方图和上面介绍的 3*1 的向量归一化一样。这想法并没有错,但是更好的方式是用一个更大尺寸 16*16 的块去归一化;
也就是 36*1 的直方图可以看成 4 个 9*1 的直方图构成,然后窗口以 8 像素移动(见上图),计算出归一化的 36*1 大小的向量然后重复这个过程遍历图像。
可视化 HOG
通过在 8*8 子图像里面进行 9*1 归一化的直方图,我们可以可视化子图像的 HOG 的描述子。
在下图中你会发现,直方图的 Dominant direction / 主要方向 捕获了这个人的外形,尤其在躯干和腿。
不幸的是,在 OpenCv 中进行 HOG 的特征描述子的可视化比较困难。

# 英文版权 @
# 翻译中文版权 @ coneypo
# 转载请注明出处



 浙公网安备 33010602011771号
浙公网安备 33010602011771号