算法第三章上机实践报告

一、实践题目名称

　　7-1 最大子段和

 

1.1 问题描述

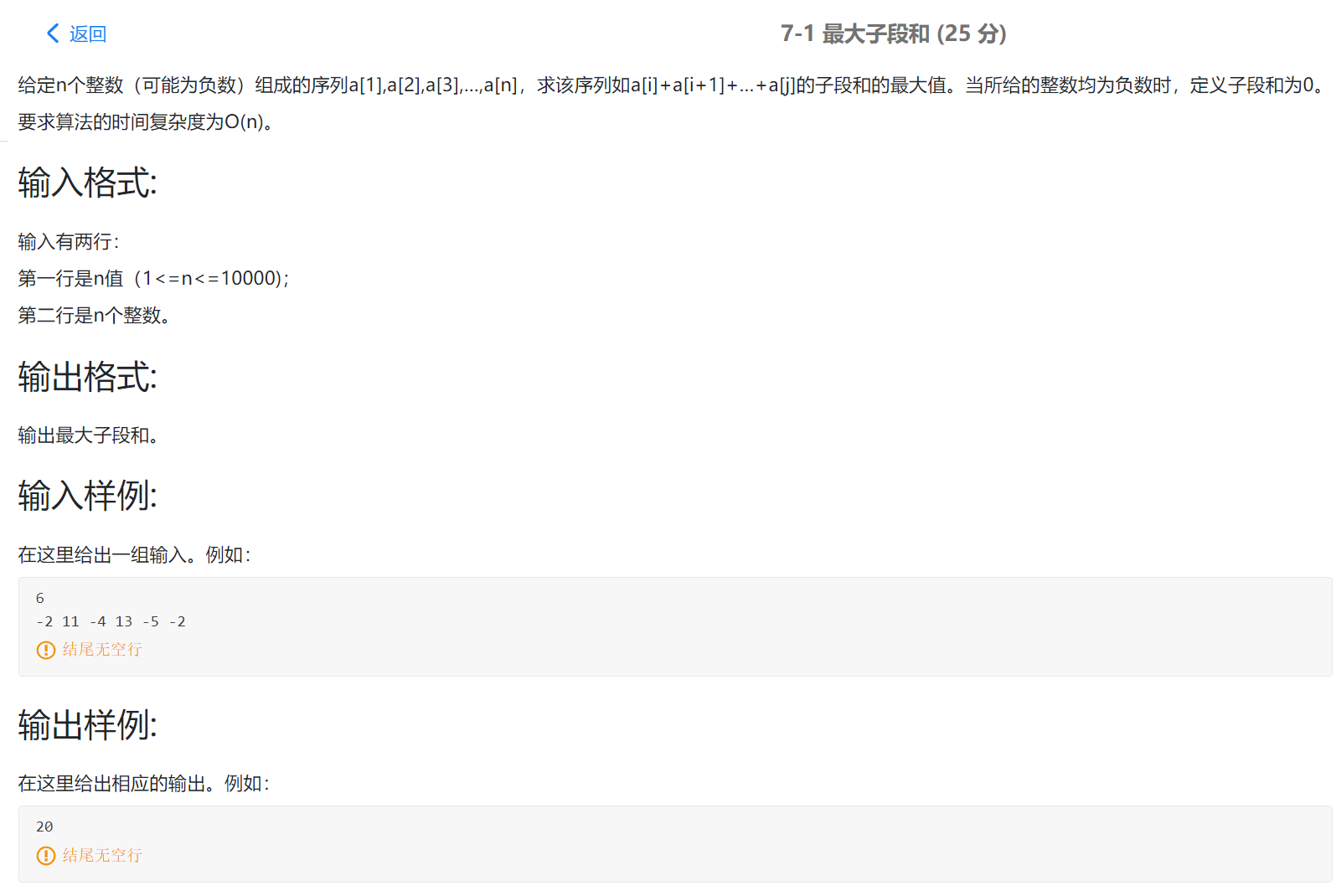
 　　简单来说，就是求由n个整数组成的序列的最大子段和

 

1.2 算法描述

　　由于题目限定该题时间复杂度为O(n)，所以无法运用传统的多重for循环方法以及分治算法来实现，不过此时我们可以考虑用动态规划的思想来实现。

 

　　算法思想为：

　　D[i]是以第i个数开头到第n个数的最大子段和。如以题目为例：D[1]={-2 11 -4 13 -5 -2} , D[2]={11 -4 13 -5 -2} ...

所需要找到的最优解为MaxSum=max{D[i]} (1<=i<=n)

 

 　　递归方程为：

　　①当D[i+1]<=0时：D[i]=a[i];

　　②当D[i+1]>0时：  D[i]=a[i]+D[i+1];

 

　　递归边界：

　　由于该算法是通过递归实现，所以要考虑递归的边界，该算法的边界为D[n]。

　　D[n]表示从第n个数开始到第n个数的字段和，此时只有一个数。

则依题可知：

　　①当a[n]<=0时：D[n]=0      //题目提到，当所给所有字段和均为负数，则定义字段和为0

　　②当a[n]>0时：  D[n]=a[n]

 

1.3 问题求解：

1.3.1 根据最优子结构性质，列出递归方程式

　　①当D[i+1]<=0时：D[i]=a[i];

　　②当D[i+1]>0时：  D[i]=a[i]+D[i+1];

 

1.3.2 给出填表法中表的维度、填表范围和填表顺序

　　表的维度：一维

　　填表范围：从1~n

　　填表顺序：从右往左，从底自上

 

1.3.3 分析该算法的时间和空间复杂度

　　时间复杂度：O(n)

　　由于该算法只遍历了一次数组（只使用了一次for循环），所以该算法地时间复杂度为O(n)

 

　　空间复杂度：O(n)

　　因为运用了数组a[n]和D[n]来记录数据，所以该算法的空间复杂度为O(n)

 

1.3 心得体会（对本次实践收获及疑惑进行总结）

　　在本次实验课上，我收获颇多。与搭档的再次合作，进一步地提高了我对合作打代码这种模式的熟悉度，并且与搭档的讨论中，解决了许多我未曾想到过的问题。如对于7-1最大子段和这一题，虽然递归方程式当中运用了D[i]数组记录数据，当实际操作时，只需要一个变量就能解决。此外，在处理这一题时，我总是惯性思维地觉得应该从左往右填表，但是这个与动态规划的划分多个子问题理念不合，因此我一开始的递归方程式是错误的。不过多亏搭档的及时提醒，自己才能尽快修改并通过。

 

2. 你对动态规划算法的理解和体会

　　动态规划主要可以分为4个步骤：问题结构分析、递归关系建立、自底向上计算、最优方案追踪。个人认为，做这类题目时，最重要的就是找到递归方程式，并且在此基础上进行深一步的简化，看看能否进一步优化算法。此外，还要注意递归边界的判断，不要在细节方面出差错。