Macacher（马拉车）算法

关于Macacher算法，以前只知道一个模板，现在在理解的基础上记录一下它的思路

对于求字符串的回文子串的常见方法有：

1 暴力求解，即枚举中点，然后向左右扩散。

2 可以将字符串反转，然后通过dp求两个字符串的最长公共子序列。

这两种方法的时间复杂度都是O(n^2)。

Manacher算法充分用到了回文串的完全对称性，可以在O(n)的时间复杂度内求处字符串的最长回文子串。

回文串大致可以分为两种，奇回文和偶回文， 为了方便处理，马拉车算法将这两种回文串变为一种后再进行处理。如何变为一种呢？

例如：

 abcdcba

 #a#b#c#d#c#b#a#

在每个字符前后都加上#(不一定非要#，只要是没出现过的字符就可以了)

这样无论原来字符串是奇数还是偶数，新的字符串都是奇数，假如说之前存在回文串abba，加上#后就会变成#a#b#b#a#，长度为2x+1所以，新的字符串出现的回文串一定是奇数的。

然后我们定义一个数组p[i]，在新的字符串中，p[i]表示以i为中心的最大回文半径(包括i)。

i       0 1 2 3 4 5 6 7 8 9 10 11 12 13
arr[i]  $ # c # a # b # b # a  #  f  #
p[i]      1 2 1 2 1 2 5 2 1 2  1  2  1

我们可以发现以i为中心的回文串的长度为(2*p[i]-1-1)/2，减去第一个1是p[i]乘以2后，多算了一个i，减去第二个1是减去最后一个位置的#,然后除以2，就是回文串的实际长度了，
也就是p[i]-1，然后就是求p数组，另外定义mx和id，表示从1~i的回文串可到达的最右端，id是该回文串中心位置。
核心部分：p[i] = mx > i ? min(p[2*id-i], mx-i) : 1;

 

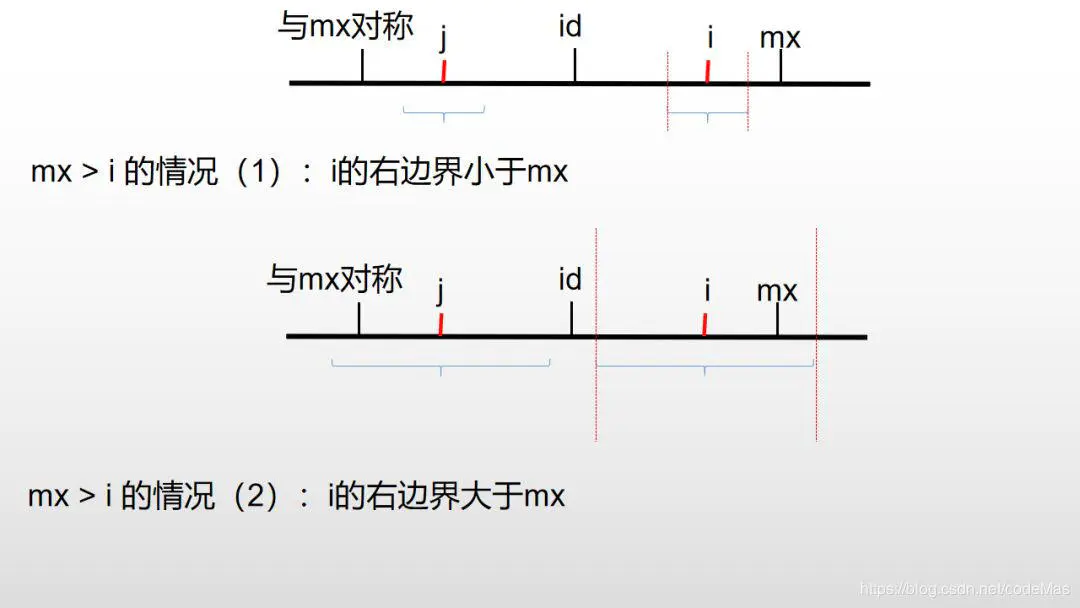
当i>mx的时候，p[i]=1;

当i<=mx的时候，可能会出现上述两种情况，j是i关于id的对称点.2*id-i。那么p[i]可完全由p[j]来决定，第一种情况就是以i为中新的回文串包含在以id为中心的回文串内部，

因此，p[i]=p[j]，第二种情况是p[j]太大了，使得j的左边界超过了与mx对称的左边界，同里p[i]可能会超过mx,为什么是可能呢？因为mx右边和与mx对陈的左边字符不一样，因此p[i]我们只能取mx-i。

所以p[i]=min(p[j],mx-i)

code：

 

void countSubstrings(string s) {
        string t = "$#";
        for(int i=0; i<s.size(); i++){
            t+=s[i];
            t+="#";
        } 
        vector<int> p(t.size() , 0); 
        int ans=0;
        int mx = 0, id = 0, reCenter = 0, reLen = 0;
        for(int i=1; i<t.size(); i++){
            p[i] = mx > i ? min(mx - i , p[2*id - i]) : 1;
            while(t[i + p[i]] == t[i - p[i]]) p[i]++;
            if(i+p[i] > mx){
                mx = i+p[i];
                id = i;
            }
        } 
    }