NOIP #1

题目。

T1

题面

给定正整数 $n$，求有多少三元组 $(a,b,c)$ 满足：

$a+b+c=n$
$1\le a<b<c\le n$
$a$ 是 $b$ 的因数，$b$ 是 $c$ 的因数

$1\le n\le 10^9$。

题解

$b=k_1\times a,c=k_2\times b=k_1\times k_2\times a$

$a+k_1\times a+k_1\times k_2\times a=n$

枚举 $a$，是 $O(d(n))$ 的。

$1+k_1+k_1\times k_2=\frac{n}{a}$

$k_1+k_1\times k_2=\frac{n}{a}-1$

$k_1\times (k_2+1)=\frac{n}{a}-1$

枚举 $\frac{n}{a}-1$ 的因数，由题意得 $k_1,k_2>1$，判断一下即可。

时间复杂度保证可以通过 $1e9$ 的数据。

代码

点击查看代码

#include<bits/stdc++.h> 
using namespace std; 
#define ll long long 
#define For(i,l,r) for(int i=l;i<=r;i++) 
ll n,ans,k1,k2;
int main(){ 
    // freopen("Autumn_Rain.in","r",stdin);
    // freopen("Autumn_Rain.out","w",stdout);
    ios::sync_with_stdio(0); 
    cin.tie(0);cout.tie(0); 
    cin>>n;
    For(i,1,n/3){
        if(n%i)continue;
        int t=n/i;
        t--;
        //k1(1+k2)=t
        for(int j=1;j*j<=t;j++){
            if(t%j)continue;
            int x=t/j;
            k1=j;k2=x-1;
            if(k1>1&&k2>1){
                ans++;
            }
            if(j*j!=t){
                x=j;
                k1=t/j;k2=x-1;
                if(k1>1&&k2>1){
                    ans++;
                }
            }
        }
    }
    cout<<ans;
    return 0; 
}

T2

题面

二维平面上有 $n$ 个点 $(x,y)$，且 $1\le x,y\le N$，每个点是黑色或白色。对于一个矩形（可以退化为线段或单点），定义其权值为其中黑点个数与白点个数的乘积。现在让矩形的上下和左右边界取遍 $1\sim N$，求所有 $\left(\frac{N(N+1)}{2}\right)^2$ 个矩形的权值和。答案对 $2^{64}$ 取模。$1\le n\le 2\times 10^5,1\le N\le 10^9,1\le x_i,y_i\le N$。

题解

选一个矩形再计算黑点白点乘积 $\rightarrow$ 选一个矩形，再选择其中的一个黑点和一个白点 $\rightarrow$ 枚举黑点 $(a,b)$ 和白点 $(c,d)$ 算有几个矩形同时包含它们。答案是：

$\operatorname{min}(a,c)\times (N-\operatorname{max}(a,c)+1)\times \operatorname{min}(b,d)\times(N-\operatorname{max}(b,d)+1)$

那么只需要对每个黑点，计算白点在左上、左下、右上、右下的权值总和，扫描线配合树状数组不难做到 $O(n\log n)$。当然要先离散化。

具体的，固定 $\operatorname{max}(a,c)=x$，原式变成：

\[(N-x+1)\times \operatorname{min}(a,c)\times\operatorname{min}(b,d)\times (N-\operatorname{max}(b,d)+1) \]

第一项固定暂时不管。然后是分类讨论当前枚举的 $y$ 是以最小值的身份做贡献，还是以最大值身份。讨论下面两种情况。

$(N-x+1)\times \operatorname{min}(a,c)\times y \times (N-\operatorname{max}(b,d)+1)$
$(N-x+1)\times \operatorname{min}(a,c)\times \operatorname{min}(b,d) \times (N-y+1)$

那么真正需要考虑的应该是：

$\sum( \operatorname{min}(a,c)\times (N-\operatorname{max}(b,d)+1))$
$\sum (\operatorname{min}(a,c)\times \operatorname{min}(b,d))$

树状数组第一维分颜色，第二维分最小最大值贡献。因为本身就给 $x$ 排序了，所以先前 add 进去的 $x$ 一定是比它小的值。可以放心食用。

代码

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define ll unsigned long long
#define For(i,l,r) for(int i=l;i<=r;i++)
const int N=2e5+10;
int n,nn;
ll ans;
struct node{
	ll x,y;bool c;
}p[N];
ll Y[N];
bool cmp(node a,node b){
	if(a.x==b.x)return a.y<b.y;
	return a.x<b.x;
}
struct BIT{
	ll t[N];
	inline void add(int x,ll v){
		for(;x<=n;x+=x&(-x)){
			t[x]+=v;
		}
	}
	inline ll qry(int x){
		ll res=0;
		for(;x;x-=x&(-x)){
			res+=t[x];
		}
		return res;
	}
	inline ll sum(int l,int r){
		return qry(r)-qry(l-1);
	}
}t[2][2];
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n>>nn;
	For(i,1,n){
		cin>>p[i].x>>p[i].y>>p[i].c;
		Y[i]=p[i].y;
	}
	sort(p+1,p+n+1,cmp);
	sort(Y+1,Y+n+1); 
	int cnt=unique(Y+1,Y+n+1)-Y-1;
	For(i,1,n)p[i].y=lower_bound(Y+1,Y+cnt+1,p[i].y)-Y;
	For(i,1,n){
		ll x=p[i].x,y=p[i].y;
		if(!p[i].c){
			ans+=(nn-x+1)*(nn-Y[y]+1)*t[1][0].sum(1,y-1);
			ans+=(nn-x+1)*Y[y]*t[1][1].sum(y,cnt);
			t[0][0].add(y,x*Y[y]);
			t[0][1].add(y,x*(nn-Y[y]+1));
		}
		else{
			ans+=(nn-x+1)*(nn-Y[y]+1)*t[0][0].sum(1,y-1);
			ans+=(nn-x+1)*Y[y]*t[0][1].sum(y,cnt);
			t[1][0].add(y,x*Y[y]);
			t[1][1].add(y,x*(nn-Y[y]+1));
		}
	}
	cout<<ans;
	return 0;
}

T3

题面

有 $n$ 个区间 $[l_i,r_i]$，其中 $1\le l_i<r_i\le m$。

现在会进行 $m$ 次操作，每次会给出 $x,s,t$，表示对 $s\le i\le t$ 的区间 $[l_i,r_i]$ 从 $x$ 处切割，保留较长的一段，两段相等时保留左侧的。具体的：

如果 $x< l_i$ 或者 $x> r_i$，则无事发生。
如果 $r_i\ge x\ge \frac{l_i+r_i}{2}$，则令 $r_i\leftarrow x$。
如果 $l_i\le x<\frac{l_i+r_i}{2}$，则令 $l_i\leftarrow x$。

求所有切割操作结束后，每个区间的左右端点。保证所有切割操作的位置 $x$ 恰好构成 $1\sim m$ 的排列。

对于所有数据：$1\le n\le 10^5,1\le m\le 10^6$。

子任务编号	$n\le $	$m\le $	特殊性质	分值
1	$5\times10^3$	$5\times10^3$	无	$10$
2	$1.6\times 10^4$	$2\times 10^5$	$AB$	$25$
3	$10^5$	$10^6$	$A$	$10$
4	$1.6\times 10^4$	$2\times 10^5$	$B$	$15$
5	$10^5$	$10^6$	$B$	$15$
6	$1.6\times 10^4$	$2\times 10^5$	无	$10$
7	$10^5$	$10^6$	无	$15$

特殊性质 A：所有 $x$ 构成 $1\sim m$ 的随机排列。

特殊性质 B：保证每次操作的 $s=1,t=n$。

题解

考虑这题简化版本，如果是保留长度较短的区间可以发现，一线段最多切 $\log$ 次。开差分数组记录每条线切割次数，暴力切割，时间复杂度 $O(n\log n)$。但是线段保留较长部分，就可能退化为 $O(nm)$ 的时间复杂度，只能得到 $10$ 分的坏成绩。

考虑子任务 2，具有 $AB$ 性质。

每个区间期望被切 $\log m$ 次。因为对于所有线段，$m$ 次每次选一个不同的 $1\sim m$ 的数字切下去。而且注意到这样构造：

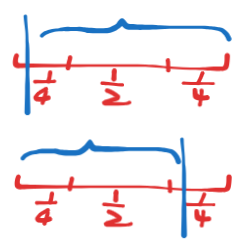
111111111

每次切割有 $\frac{1}{2}$ 的概率至少/至多变为原来的 $\frac{3}{4}$（这里我们考虑至多）。相当于两次切割变为原来的 $\frac{3}{4}$，假设一个超长区间长度为 $m$，也就是 $m\times(\frac{3}{4})^{\frac{1}{2}\times k}\le 1$，解得：期望次数 $k$ 不超过 $2\times log_{\frac{4}{3}}m$，也就是 $\log m$。这是在随机排列的情况下。如果刻意对着某个地方切就不一定了。

设 $t_i$ 表示位置 $i$ 的切割时间（因为 $x$ 是排列，不重复）。那么区间 $[l,r]$ 第一次被切的时间就是 $\operatorname{min}(t_{l+1}\sim t_{r-1})$。找到这个最小值 $t_p$ 后模拟得到的区间 $[l,p]$ 或 $[p+1,r]$，接着操作下去即可。可以用 ST 表，时间复杂度 $O(n\log m+ m\log m)$。

子任务 3，特殊性质 A。

1111111111111111111111111111

这个平方来源于每个区间期望被切 $\log m$ 次，线段树更新加上扫一遍是 $n\log m$ 的。$m$ 次询问，线段树找最小值复杂度是 $\log m$ 的。

子任务 4，5。只有 $B$ 性质。

神人注意力。

4545454

这个分段的真的是太神秘了。二分找到下一个操作以后，长度 $\times \frac{2}{3}$ 然后继续往下走，复杂度也是 $\log m$ 级别的。

复杂度里 $n$ 是扫一遍的复杂度，$\log m$ 是找 $\operatorname{min}$ 的复杂度。还有一只 $\log m$ 是区间切割次数。

没有特殊性质。

对于编号区间的限制，扫描线一下，给线段树二分加一个单点修改操作。时间复杂度 $O(n\log^2m+m\log m)$。题目略微卡常。

代码

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,l,r) for(int i=l;i<=r;i++)
const int N=1e5+10;
const int M=1e6+10;
int n,m,id;
int l[N],r[N],tim[M];
struct node{
	int x,l,r;
}q[M];
bool cmp(node a,node b){
	if(a.l==b.l)return a.r<b.r;
	return a.l<b.l;
}
vector<int>a[N];
struct Seg{
	int mn,pos;
}t[M<<2];
#define lc u<<1
#define rc u<<1|1
void pushup(int u){
	t[u].mn=min(t[lc].mn,t[rc].mn);
	if(t[lc].mn<=t[rc].mn){
		t[u].pos=t[lc].pos;
	}
	else t[u].pos=t[rc].pos;
}
void build(int u,int l,int r){
	if(l==r){
		t[u].mn=1e9;
		t[u].pos=l;
		return;
	}
	int mid=(l+r)>>1;
	build(lc,l,mid);
	build(rc,mid+1,r);
	pushup(u);
}
void upd(int u,int L,int R,int x,int v){
	if(L==R){
		t[u].mn=v;
		return;
	}
	int mid=(L+R)>>1;
	if(x<=mid)upd(lc,L,mid,x,v);
	else upd(rc,mid+1,R,x,v);
	pushup(u);
}
#define pii pair<int,int>
#define fi first
#define se second
pii qry(int u,int L,int R,int l,int r){
	pii res;
	if(l<=L&&R<=r){
		res={t[u].mn,t[u].pos};
		return res;
	}
	else if(!(r<L||l>R)){
		int mid=(L+R)>>1;
		pii lans=qry(lc,L,mid,l,r);
		pii rans=qry(rc,mid+1,R,l,r);
		res=min(lans,rans);
		return res;
	}
	else{
		res={1e9,1e9};
		return res;
	}
}
#define pb push_back
//[l,r]中min<v的最大位置 
int get(int u,int L,int R,int l,int r,int v){
	if(t[u].mn>=v)return -1;
	if(L==R)return t[u].pos;
	int mid=(L+R)>>1;
	int res=-1;
	//优先查右子树找最大位置
	if(r>mid)res=get(rc,mid+1,R,l,r,v);
	if(res!=-1)return res;
	if(l<=mid)res=get(lc,L,mid,l,r,v);
	return res;
}
//[l,r]中min<v的最小位置
int get2(int u,int L,int R,int l,int r,int v){
	if(t[u].mn>=v)return -1;
	if(L==R)return t[u].pos;
	int mid=(L+R)>>1;
	int res=-1;
	//优先查左子树找最小位置
	if(l<=mid)res=get2(lc,L,mid,l,r,v);
	if(res!=-1)return res;
	if(r>mid)res=get2(rc,mid+1,R,l,r,v);
	return res;
}
inline int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-48;c=getchar();}
    return x*f;
}
int main(){
	n=read();m=read();id=read();
	For(i,1,n){l[i]=read();r[i]=read();}
	For(i,1,m){
		q[i].x=read();
		q[i].l=read();
		q[i].r=read();
		tim[q[i].x]=i;
	}
	sort(q+1,q+m+1,cmp);
	build(1,1,m);
	int j=1;
	For(i,1,n){
		while(j<=m&&q[j].l<=i){
			upd(1,1,m,q[j].x,tim[q[j].x]);
			a[q[j].r+1].pb(q[j].x);
			j++;
		}
		for(int x:a[i])upd(1,1,m,x,1e9);
		int L=l[i],R=r[i];
		while(1){
			if(L==R-1||L>=R)break;
			int len=(R-L+1)/3;
			pii res=qry(1,1,m,L+len,R-len);
			int mn=res.fi,pos=res.se;
			int ql=get(1,1,m,1,L+len-1,mn);
			int qr=get2(1,1,m,R-len+1,R,mn);
			if(ql!=-1)L=max(L,ql);
			if(qr!=-1)R=min(R,qr);
			if(mn==1e9)break;
			if(2*pos>=L+R)R=pos;
			else L=pos;
		}
		printf("%d %d\n",L,R);
	}
	return 0;
}

T4

题面

有一张 $n$ 个点的无向图，初始图中没有任何边。

接下来不断重复以下操作：

设 $\deg_i$ 为第 $i$ 个点当前的度数（即有多少个点和它有直接连边），从所有满足 $\deg_u,\deg_v$ 中至少有一个是 $0$ 的点对 $(u,v)$ 中等概率选取一个（例如，假设当前有 $k$ 个点的度数非零，则一共有 $\binom{n}{2}-\binom{k}{2}$ 种可能选取的点对），然后加一条边 $(u,v)$。

最终无法进行操作，即不存在孤立点时停止操作。

给定 $m$，求恰好 $m$ 次操作后停止的概率，答案对给定的质数 $P$ 取模。

对于所有数据，保证 $2\le n\le 10^7,\lceil n/2\rceil \le m\le n-1,10^8\le P\le 10^9+9$，$P$ 是质数。

测试点编号	$n$	特殊性质
$1\sim 2$	$\le 5$	无
$3\sim 4$	$\le 100$	无
$5\sim 6$	$\le 4000$	无
$7\sim 9$	$\le 10^6$	$m=n-1$
$10\sim 14$	$\le 10^5$	$P=998244353$
$15\sim 17$	$\le 10^6$	无
$18\sim 20$	$\le 10^7$	无

题解

题解链接。

posted @ 2025-11-09 22:14 Accept_Reality 阅读(13) 评论(0) 收藏举报

刷新页面返回顶部

子任务编号	$n\le $	$m\le $	特殊性质	分值
1	\(5\times10^3\)	\(5\times10^3\)	无	\(10\)
2	\(1.6\times 10^4\)	\(2\times 10^5\)	\(AB\)	\(25\)
3	\(10^5\)	\(10^6\)	\(A\)	\(10\)
4	\(1.6\times 10^4\)	\(2\times 10^5\)	\(B\)	\(15\)
5	\(10^5\)	\(10^6\)	\(B\)	\(15\)
6	\(1.6\times 10^4\)	\(2\times 10^5\)	无	\(10\)
7	\(10^5\)	\(10^6\)	无	\(15\)

测试点编号	\(n\)	特殊性质
\(1\sim 2\)	\(\le 5\)	无
\(3\sim 4\)	\(\le 100\)	无
\(5\sim 6\)	\(\le 4000\)	无
\(7\sim 9\)	\(\le 10^6\)	\(m=n-1\)
\(10\sim 14\)	\(\le 10^5\)	\(P=998244353\)
\(15\sim 17\)	\(\le 10^6\)	无
\(18\sim 20\)	\(\le 10^7\)	无

AcceptReality

NOIP #1

T1

题面

题解

代码

T2

题面

题解

代码

T3

题面

题解

代码

T4

题面

题解