最小生成树算法——Prim算法 Kruskal算法

给定一个无向图，要去掉一些边使得边上权值加和最小，同时任意两个顶点互相连通。

显然最后把边去掉后只会剩下一个树。

Prim算法：

vis数组用于记录是否已访问该顶点。

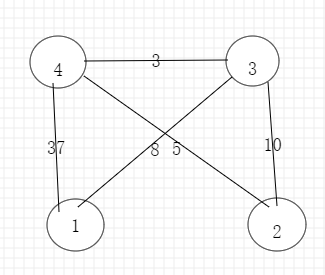
比如从1顶点出发，那么dis数组存的即为1到其他顶点的距离，也就是dis[1]=0,dis[3]=8,dis[4]=37

此时无法到达2节点，所以dis[2]=inf(很大的一个数）

此时vis[1]=1就视1已加入生成树中。此时会从dis数组找一个最小的dis[ i ]并且 i 节点未加入生成树中

也就是vis[ i ]=0；

下个加入树中的节点为 3 此时total=8；

然后vis[3]=1表示加入树中，更新dis数组，dis[ 2 ]=10 dis[ 4 ]=3

那么按照以小的原则，下一个加入的节点就是4 total=8+3

然后更新dis[ 2 ]=5。

最后加入2节点 total=8+3+5

 1 const int inf = 0x3f3f3f3f;
 2 int dis[5010], vis[5010], e[5010][5010];
 3 int prim(int n)
 4 {
 5     int i, j, v, min = 0, total = 0, p = 0;
 6     for (i = 1; i <= n; i++)//初始化
 7     {
 8         dis[i] = e[1][i];
 9         vis[i] = 0;
10     }
11     vis[1] = 1;
12     for (j = 1; j < n; j++)
13     {
14         min = inf;
15         for (i = 1; i <= n; i++)
16         {
17             if (vis[i] == 0 && dis[i] < min)
18             {
19                 min = dis[i];
20                 v = i;
21             }
22         }
23         if (min == inf)
24             break;
25         vis[v] = 1, total += dis[v];
26         for (p = 1; p <= n; p++)
27         {
28             if (vis[p] == 0 && dis[p] > e[v][p])
29                 dis[p] = e[v][p];
30         }
31     }
32     return total;
33 }

考虑到在找加入到生成树中的节点时找的是权值最小的边，因此可以考虑用堆优化

Prim算法（堆优化）：

counter用来记录已加入树中的节点

 1 const int inf = 0x3f3f3f3f;
 2 int dis[100010], vis[100010], head[100010];
 3 int p;
 4 struct edge
 5 {
 6     int to, next, w;
 7 }e[20010];
 8 void add(int s, int t, int w)
 9 {
10     e[++p].to = t;
11     e[p].next = head[s];
12     head[s] = p;
13     e[p].w = w;
14 }
15 struct Edge
16 {
17     int dis, to;
18     Edge(int a, int b) :dis(a), to(b) {};
19     bool operator <(const Edge&k)const
20     {
21         return dis > k.dis;
22     }
23 };
24 int prim(int n)
25 {
26     int i, j;
27     int sum = 0;
28     int counter = 0;
29     for (i = 1; i <= n; i++)
30     {
31         vis[i] = 0;
32         dis[i] = inf;
33     }
34     dis[1] = 0;
35     priority_queue<Edge>q;
36     q.push(Edge(0, 1));
37     while (q.size() && counter < n)
38     {
39         Edge t = q.top(); q.pop();
40         if (!vis[t.to])
41         {
42             counter++;
43             vis[t.to] = 1; sum += dis[t.to];
44             for (i = head[t.to]; i > 0; i = e[i].next)
45             {
46                 if (dis[e[i].to] > e[i].w)
47                 {
48                     dis[e[i].to] = e[i].w;
49                     q.push(Edge(dis[e[i].to], e[i].to));
50                 }
51             }
52         }
53     }
54     return sum;
55 }

Kruskal算法：

kruskal是基于边的，每次把权值最小的边加入生成树中，用并查集来将节点归为一个集合

当边的两个节点处于同一个并查集时，就不加入该边。

还是上图，一开始会按边 3 5 8 10 37 排列，

并且f [ i ] = i，即任意两个点不在同一集合

然后会加入权值为3的边此时会有f[ 4 ]=3 (或 f [ 3 ]=4)表示3 4节点处在同一并查集中

然后是权值为5的边此时会将｛3，4｝和｛2｝合并，就这样直到所有点都在同一集合后

得到的res即为最小生成树的值

 1 struct edge{int u,v,cost;};
 2 
 3 bool cmp_(edge a,edge b)
 4 {
 5     return a.cost<b.cost;
 6 }
 7 
 8 edge e[10010];
 9 int f[10010];
10 int V,E;// V是点数  E是边数
11 
12 int find_(int x)
13 {
14     if(x==f[x])return x;
15     return f[x]=find(f[x]);
16 }
17 int change_(int a,int b)
18 {
19     int x=find_(a),y=find_(b);
20     if(x!=y)
21         f[y]=x;
22 }
23 int kruskal()
24 {
25     int i,j;
26     sort(e+1,e+1+E,cmp_);//按边从小到大排列
27     for(i=1;i<=V;i++)
28         f[i]=i;
29     int res=0;
30     for(i=1;i<=E;i++)
31     {
32         if(find_(e[i].u)!=find_(e[i].v))//若不在一个集合则加入该边并将两个点的集合合并
33         {
34             change_(e[i].u,e[i].v);
35             res+=e[i].cost;
36         }
37     }
38     return res;
39 }

posted on 2020-12-14 19:46 丶蛋花拉面阅读(63) 评论(0) 收藏举报