[学习笔记] 生成函数

目录

0. 前置芝士

0.1. 导数

0.1.1. 常用导数

\[(a^x)'=a^x\ln a \]

特别地，\((e^x)'=e^x\ln e=e^x\).

\[(\sin x)'=\cos x \]

\[(\cos x)'=-\sin x \]

\[(x^a)'=ax^{a-1} \]

\[(\ln x)'=\frac{1}{x} \]

一个总结性公式

\[(x^a)^{(n)}=\frac{a!}{(a-n)!}x^{a-n} \]

0.1.2. 运算法则

  • 加减可以直接拆开。

  • 乘法：

    \[(f(x)g(x))'=f(x)'g(x)+f(x)g'(x) \]

  • 除法：

    \[(f(x)\div g(x))'=\frac{f(x)'g(x)-f(x)g'(x)}{g^2(x)} \]

0.2. 泰勒展开

详情请见 [干饭现场] 多项式全家桶。

1. 普通生成函数（\(\rm OGF\)）

1.1. 定义

对于一个无穷序列 \(\{a_0, a_1, a_2,...\}\)，定义其普通生成函数为形式幂级数：\(\sum_{k=0}^{\infty}a_kx^k\).

1.2. 常用普通生成函数

1.2.1. 斐波那契数列

首先可以推导出它的封闭形式。

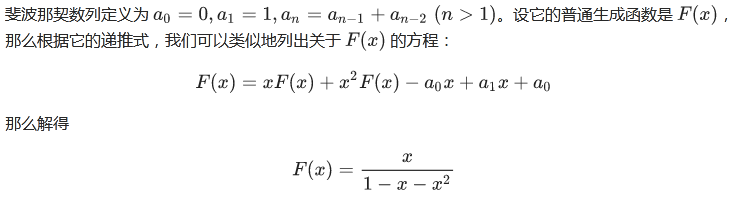
在泰勒展开的 0.1.2. 一些常见的展开 中，我们已经推导出 \(\frac{1}{(1-x)^{a+1}}\) 的展开。所以可以尝试利用它来展开 \(F(x)\).

比方说，考虑 $\frac{A}{1-ax}$ 的形式可以写成幂级数 $A\sum_{n\ge 0}(ax)^n$，我们可以将 $1-x-x^2$ 进行因式分解成 $(1-ax)(1-bx)$ 的形式。

或者，也可以使用整体法，不用因式分解，直接硬套。

1.2.2. 广义五边形数

1.2.2.1. 基本公式与定理

证明部分略去不讲。

  • 广义五边形数的通项公式为

\[p_n=\frac{n(3n\mp 1)}{2} \]

  • 定义欧拉函数为

    \[\phi(x)=\prod_{i=1}^{\infty} (1-x^i) \]

    五边形数定理即为

    \[\phi(x)=\sum_{i=0}^{\infty} (-1)^i\cdot x^{\frac{i(3i\mp 1)}{2}} \]

    \(\rm hint\)：\(\phi(x)\) 的第 \(n\) 项系数就是 "将 \(n\) 拆成偶数个正整数的方案数 \(-\) 将 \(n\) 拆成奇数个正整数的方案数"。注意这里拆分出来的数字 两两不同。

1.2.2.2. 整数拆分

定义 \(p_n\) 表示把 \(n\) 拆分成若干个 可以相等 的整数的方案数。由此设计出 \(p_n\) 的生成函数

\[F(x)=\sum_{i=1}^{\infty} p_i\cdot x^i=\prod_{i=1}^{\infty}(1+x^i+x^{2i}+\cdots)=\prod_{i=1}^{\infty} \frac{1}{1-x^i} \]

很容易发现有 \(F(x)\phi(x)=1\)。于是可以构造出 \(\phi(x)\) 然后直接多项式求逆做到 \(\mathcal O(n\log n)\).

如果并不要求更优秀的复杂度的话，我们可以暴力展开第 \(n\) 项的系数（右边由于只有常数项，所以系数为零）

\[p_n-p_{n-1}-p_{n-2}+p_{n-5}+p_{n-7}-\dots =0 \]

函数传入的值实际上是 \(n\) 减去广义五边形数。由于广义五边形数的增长速度是 \(n^2\) 的，所以可以递推 \(p\) 数列，单次递推 \(\mathcal O(\sqrt n)\)，总复杂度 \(\mathcal O(n\sqrt n)\).

1.2.3. 卡特兰数列

\(\mathcal{P}{\rm ortal.}\)

2. 指数生成函数（\(\rm EGF\)）

2.1. 定义

对于一个无穷序列 \(\{a_0, a_1, a_2,...\}\)，定义其指数生成函数为形式幂级数：\(\sum_{k=0}^{\infty}a_k\cdot \frac{x^k}{k!}\).

指数生成函数乘法的意义：🔗

2.2. 常用指数生成函数

  • \(\{1,1,1,1,1\dots\}\xrightarrow{\bf EGF}e^x\)；
  • \(\{1,-1,1,-1,1\dots\}\xrightarrow{\bf EGF}e^{-x}\)；
  • \(\{1,c,c^2,c^3\dots\}\xrightarrow{\bf EGF}e^{cx}\)；
  • \(\{1,0,1,0,1,0\dots\}\xrightarrow{\bf EGF}\dfrac{e^x+e^{-x}}{2}\)；
  • \(\{1,a,a^{\underline 2},a^{\underline 3},a^{\underline 4}\dots\}\xrightarrow{\bf EGF}(1+x)^a\)，同时这个序列第 \(i\) 项的意义是 \(a\) 个元素的 \(i\) 排列数，也就是 \(\text{C}(a,i)\cdot i!\).

2.3. 可爱的例题们

例 1：有 \(8\) 个元素，其中有 \(3\) 个 \(a_1\)，\(2\) 个 \(a_2\)，\(3\) 个 \(a_3\)。从中取 \(6\) 个元素，求可能的排列数。

\[\hat G(x)=\left(1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}\right)\cdot\left(1+\frac{x}{1!}+\frac{x^2}{2!}\right)\cdot \left(1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}\right)\\ \]

除以阶乘相当于去除内部元素的顺序，最终将 \(x^i\) 项前的系数统一提出 \(\frac{1}{i!}\)，分子就是取 \(i\) 个元素的排列数。考虑提出 \(\frac{1}{i!}\) 相当于给分子乘上 \(i!\).

例 2：带标号无向连通图计数。

首先设 \(f_i\) 表示 \(i\) 个点的有标号连通图个数，\(g_i\) 表示 \(i\) 个点的任意图个数，那么 \(g_i = 2^{\text{C}(i,2)}\).

设 \(f_i\) 的指数生成函数为 \(F(x)\)，\(g_i\) 的指数生成函数为 \(G(x)\)。那么有

\[G(x)=\sum_{i\geqslant 1} \dfrac{F^i(x)}{i!} \]

考虑证明。假设点个数为 \(n\)，分为大小为 \(a_1, a_2, \dots , a_k\) 的组。首先分配标号，系数为 \(\dfrac{n!}{\prod_{i=1}^k a_i!}\)，于是有

\[g_n = \sum_{k\geqslant 1} \frac{1}{k!}\cdot \left(\sum_{\sum a_i=n}\frac{n!}{\prod_{i=1}^k a_i!}\cdot \prod_{i=1}^k f_{a_i} \right) \]

前面的 \(1/k!\) 是将划分出的图的标号去除。化一下柿子得

\[\dfrac{g_n}{n!} = \sum_{k\geqslant 1} \frac{1}{k!}\cdot \left(\sum_{\sum a_i=n}\prod_{i=1}^k \dfrac{f_{a_i}}{a_i!} \right) \]

大括号那一坨是 \([x^n] F^k(x)\)。于是

\[\dfrac{g_n}{n!} = \sum_{k\geqslant 1} \dfrac{[x^n]F^k(x)}{k!} \Leftrightarrow G(x) = \sum_{k\geqslant 1} \dfrac{F^k(x)}{k!} \]

可以发现上面的 \(\dfrac{F^k(x)}{k!}\) 就是 \(e^{F(x)}\) 的泰勒展开，所以有

\[G(x) = \exp F(x) \Leftrightarrow F(x) = \ln G(x) \]

所以求出 \(G(x)\) 后再多项式求 \(\ln\) 即可得到答案。另外容易发现这个结论也可以结合 \(\rm pruefer\) 序列应用于生成树计数。

哦哟还可以发现这也是排列与圆排列的关系。同时还可以根据这个推导错排数的指数生成函数：考虑错排就是置换环中不存在自环的排列，先构造 "置换环不存在自环的圆排列" 的指数生成函数

\[\sum_{n\geqslant 2}\frac{(n-1)!\cdot x^n}{n!}=\sum_{n\geqslant 2}\frac{x^n}{n}=-\ln(1-x)-x \]

于是错排数的 \(\mathtt{EGF}\) 就是 \(\exp(-\ln(1-x)-x)\).

例 3：给出 \(n\)，在 有哈密顿回路的 \(n\) 个点的竞赛图中等概率选出一个，求哈密顿回路个数的期望。

首先对期望进行转化，就是所有 \(n\) 个点的竞赛图中哈密顿回路数量总和除以有哈密顿回路的 \(n\) 个点的竞赛图数量。

第一个部分是比较好计算的，就是 \((n-1)!\cdot 2^{\text{C}(n,2)-n}\)，也就是枚举哈密顿回路，再枚举其它边。

而关于有哈密顿回路的 \(n\) 个点的竞赛图数量，这里有个结论：一张竞赛图有哈密顿回路的充要条件是它是强连通的。证明我翻了翻网上的一些博客，也许是没有 get 到关键，感觉有些证明有些伪，所以现在就咕咕咕了（。

设 \(f_i\) 为 \(n\) 个点且强连通的竞赛图数量，可以正难则反

\[f_n=2^{\text{C}(n,2)}-\sum_{i=1}^{n-1}f_i\cdot \binom{n}{i}\cdot 2^{\text{C}(n-i,2)} \]

再移项得

\[2^{\text{C}(n,2)}=\sum_{i=1}^{n}f_i\cdot \binom{n}{i}\cdot 2^{\text{C}(n-i,2)} \]

右式类似卷积，用 \(\mathtt{OGF}\) 描绘中间的组合数是不易的。但考虑 \(\dbinom{n}{i}=\dfrac{n!}{i!(n-i)!}\)，这实际上就明示使用 \(\mathtt{EGF}\) 了！所以令

\[F(x)=\sum_{i=1}^{\infty} \frac{f_i}{i!}\cdot x^i,G(x)=\sum_{i=0}^{\infty} \frac{2^{\text{C}(i,2)}}{i!}\cdot x^i \]

把这两个函数卷起来（注意特判 \(i=0\) 的情况）

\[G(x)=F(x)G(x)+1 \]

多项式求逆即可求解 \(G(x)\).

posted on 2021-02-18 22:02  Oxide  阅读(196)  评论(0)    收藏  举报