BZOJ - 3512 DZY Loves Math IV

题意

求 。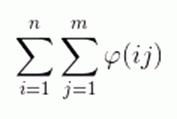

其中 \(n\le10^5,m\le 10^9\)。

解法

先开始没有注意到 \(n\) 比较小，拿着柿子就开始硬刚，刚出了这么个脑瘫产物：\(\sum_{i=1}^{n\times m}\varphi(i)d_0(i)\)。

不仅上界那么大，还没有办法用杜教筛（\(\varphi(i)\) 和 \(d_0(i)\) 都没有办法用简单函数 \(f\left(\frac{n}{i}\right)\) 来搞掉）。

不过这里有个结论：

若 \(m\) 的质因子种类包含在 \(n\) 的质因子种类中，那么 \(\varphi(n\times m)=\varphi(n)\times m\)。

证明用欧拉函数的展开式即可。

我们设 \(S(n,m)=\sum_{i=1}^m \varphi(n\times i)\)，令 \(n'\) 为 \(n\) 的所有种类质因子的乘积，\(n’'=\frac{n}{n'}\)。那么就有 \(S(n,m)=n''\sum_{i=1}^m \varphi(n'\times i)\)。由于答案是 \(\sum_{i=1}^nS(i,m)\)，为了方便算，我们将每个 \(i\) 的 \(i''\) 提出来，将 \(i’\) 代入 \(S\)。

\[\sum_{i=1}^m \varphi(n\times i)=\sum_{i=1}^m \varphi(\frac{n}{\gcd(n,i)}\times i\times \gcd(n,i)) \]

由于 \(n\) 的质因子指数均为 \(1\)，所以 \(\frac{n}{\gcd(n,i)}\) 与 \(\gcd(n,i)\) 互质，又因为 \(\frac{n}{\gcd(n,i)}\) 与 \(i\) 显然互质，故 \(\frac{n}{\gcd(n,i)}\) 和 \(i\times \gcd(n,i)\) 互质，可以拆开。

\[=\sum_{i=1}^m \varphi(\frac{n}{\gcd(n,i)})\times \varphi(i\times \gcd(n,i)) \]

\[=\sum_{i=1}^m \varphi(\frac{n}{\gcd(n,i)})\times \varphi(i)\times \text{id}(\gcd(n,i)) \]

\[=\sum_{i=1}^m \varphi(\frac{n}{\gcd(n,i)})\times \varphi(i)\times \sum_{d|\gcd(n,i)}\varphi(d) \]

\(\frac{n}{\gcd(n,i)}\) 与 \(\gcd(n,i)\) 的因子互质，故：

\[=\sum_{i=1}^m \varphi(i)\times \sum_{d|\gcd(n,i)}\varphi(\frac{n}{\frac{\gcd(n,i)}{d}}) \]

\[=\sum_{i=1}^m \varphi(i)\times \sum_{d|n,d|i}\varphi(\frac{n}{d}) \]

枚举 \(d\)，

\[=\sum_{d=1}^n\varphi(\frac{n}{d})\sum_{i=1}^{\frac{m}{d}} \varphi(i\times d) \]

\[=\sum_{d=1}^n\varphi(\frac{n}{d})S(d,\frac{m}{d}) \]

这样就可以记忆化搜索了，边界就是 \(n=1\)，此时 \(S(1,m)\) 就是欧拉函数前缀和，用杜教筛即可。

代码

#include <cstdio>

#define rep(i,_l,_r) for(register signed i=(_l),_end=(_r);i<=_end;++i)
#define fep(i,_l,_r) for(register signed i=(_l),_end=(_r);i>=_end;--i)
#define erep(i,u) for(signed i=head[u],v=to[i];i;i=nxt[i],v=to[i])
#define efep(i,u) for(signed i=Head[u],v=to[i];i;i=nxt[i],v=to[i])
#define print(x,y) write(x),putchar(y)

template <class T> inline T read(const T sample) {
    T x=0; int f=1; char s;
    while((s=getchar())>'9'||s<'0') if(s=='-') f=-1;
    while(s>='0'&&s<='9') x=(x<<1)+(x<<3)+(s^48),s=getchar();
    return x*f;
}
template <class T> inline void write(const T x) {
    if(x<0) return (void) (putchar('-'),write(-x));
    if(x>9) write(x/10);
    putchar(x%10^48);
}
template <class T> inline T Max(const T x,const T y) {if(x>y) return x; return y;}
template <class T> inline T Min(const T x,const T y) {if(x<y) return x; return y;}
template <class T> inline T gcd(const T x,const T y) {return y?gcd(y,x%y):x;}
template <class T> inline T lcm(const T x,const T y) {return x/gcd(x,y)*y;}
template <class T> inline T fab(const T x) {return x>0?x:-x;}
template <class T> inline T Swap(T &x,T &y) {x^=y^=x^=y;}

#include <map>
using namespace std;

const int mod=1e9+7,maxn=1e5+5,lim=1e6;

int n,m,pre[lim+5],phi[lim+5],low[lim+5],Ans,p[maxn],pc;
bool is[lim+5];
map <int,int> ans[maxn],mp;

void inc(int &x,int y) {
	x=x+y;
	if(x>=mod) x=x-mod;
}

void dec(int &x,int y) {
	x=x-y;
	if(x<0) x=x+mod;
}

void sieve() {
	phi[1]=low[1]=1;
	rep(i,2,lim) {
		if(!is[i]) p[++pc]=i,phi[i]=i-1,low[i]=i;
		rep(j,1,pc) {
			if(i*p[j]>lim) break;
			is[i*p[j]]=1;
			if(i%p[j]) phi[i*p[j]]=phi[i]*(p[j]-1),low[i*p[j]]=low[i]*p[j];
			else {
				phi[i*p[j]]=phi[i]*p[j],low[i*p[j]]=low[i];
				break;
			}
		}
	}
	rep(i,1,lim) pre[i]=(pre[i-1]+phi[i])%mod;
}

int Phi(int n) {
	if(n<=lim) return pre[n];
	if(mp.count(n)) return mp[n];
	int ret=1ll*(n+1)*n/2%mod,r;
	for(int l=2;l<=n;l=r+1) {
		r=(n/(n/l));
		dec(ret,1ll*(r-l+1)*Phi(n/l)%mod);
	}
	mp.insert(make_pair(n,ret));
	return ret;
}

int S(int n,int m) {
	if(!m) return 0;
	if(n==1) return Phi(m);
	if(ans[n].count(m)) return ans[n][m];
	int ret=0;
	for(int i=1;i*i<=n;++i)
		if(n%i==0) {
			inc(ret,1ll*phi[n/i]*S(i,m/i)%mod);
			if(i*i^n) inc(ret,1ll*phi[i]*S(n/i,m/(n/i))%mod);
		}
	ans[n].insert(make_pair(m,ret));
	return ret;
}

int main() {
	n=read(9),m=read(9);
	sieve();
	rep(i,1,n) inc(Ans,1ll*i/low[i]*S(low[i],m)%mod);
	print(Ans,'\n');
	return 0;
}