1. \(\text{exkmp}\)
2. \(\rm kmp\) 的各种应用
2.1. 在字符串中查找子串
给定一个文本 \(t\) 和一个字符串 \(s\),找到并展示 \(s\) 在 \(t\) 中的所有出现。
在 \(s\) 与 \(t\) 之间插入分隔符,再 \(\rm kmp\) 一遍,最后询问 \(t\) 中 \(\rm nxt\) 值为 \(|s|\) 的位置即可。
2.2. 字符串压缩
3. \(\rm border\) & \(\rm period\)
3.1. 定义
若 \(s\) 长度为 \(r\) 的前缀与长度为 \(r\) 的后缀相等,称 \(s\) 长度为 \(r\) 的前缀为 \(s\) 的 \(\rm border\).
若 \(0<p\leq |s|,s_i=s_{i+p},\forall i\in[1,|s|-p]\),则称 \(p\) 为 \(s\) 的一个 \(\text{period}\).
显然,\(r\) 为 \(\text{border} \iff |s|-r\) 为 \(\text{period}\). 这样利用 \(\rm kmp\) 可以在 \(\mathcal O(n)\) 时间内计算出 \(s\) 所有的周期,显然 \(|s|-\text{nxt}_{|s|}\) 是 \(s\) 的最小周期。
3.2. 引理
\(\text{Weak Periodicity Lemma}\):若 \(p\) 和 \(q\) 是 \(s\) 的周期,\(p+q≤|s|\),则 \(\gcd(p,q)\) 也为 \(s\) 的周期。
\(\cal Proof\):不妨设 \(p<q\),记 \(d=q-p\). 对于 \(i\in[1,|s|-d]\),我们进行分类讨论
- 若 \(i\le p\):此时有 \(i+q\le |s|\),所以有 \(s_i=s_{i+q}=s_{i+q-p}=s_{i+d}\);
- 若 \(i>p\):此时 \(i-p\ge 1\),所以有 \(s_i=s_{i-p}=s_{i-p+q}=s_{i+d}\).
综上,\(d\) 为 \(s\) 的一个 \(\rm period\). 利用错位相减法即可得到 \(\gcd(p,q)\) 为 \(s\) 的周期。
\(\text{Periodicity Lemma}\):若 \(p\) 和 \(q\) 是 \(s\) 的周期,\(p+q-\gcd(p,q)≤|s|\),则 \(\gcd(p,q)\) 也为 \(s\) 的周期。
3.3. 定理
\(\text{Theorem 1}\):若字符串 \(s,t\) 满足 \(|s|≥|t|/2\),则 \(s\) 在 \(t\) 中所有匹配位置构成一个等差数列,公差为 \(s\) 的最小周期。
\(\cal Proof\):
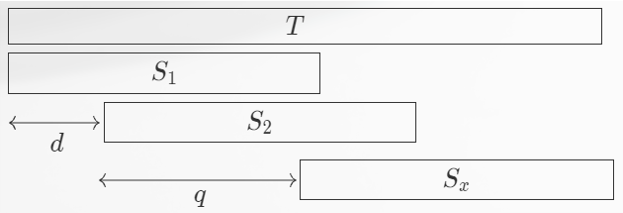
首先对于小于三的匹配数一定构成等差序列,这里不予讨论。
设第一,二次匹配间隔长度为 \(d\),之后的某次匹配 \(x\) 与第二次匹配的间隔为 \(q\). 由于 \(S_1,S_2\) 可以看作 \(S_1 \cup S_2\) 的前后缀 \(\rm border\),所以 \(d\) 为 \(S_1\cup S_2\) 的周期,那么易证 \(d,q\) 均为 \(s\) 的周期。由于 \(|s|≥|t|/2\),任意两个匹配要么有交要么紧贴,所以 \(d+q\le |s|\),由引理可知 \(r=\gcd(d,q)\) 也是 \(s\) 的周期。
设 \(s\) 的最小周期为 \(p\),显然 \(p\le r\),那么有 \(p\mid r\mid d\),否则由引理可以构造 \(\gcd(p,r)\) 为 \(s\) 更小的周期。由于 \(d\) 为 \(S_1\cup S_2\) 的周期,所以 \(p\) 也为 \(S_1\cup S_2\) 的周期。若 \(p<d\),那么由于 \(p\) 为 \(S_1\cup S_2\) 的周期,可以构造出比 \(S_2\) 更靠近 \(S_1\) 的匹配,矛盾。所以 \(p=r=d=\gcd(d,q)\),那么 \(q\) 为 \(d\) 的整数倍。对于两个匹配 \(S_x,S_y\),假设间隔为 \(q\),由 \(q\) 为 \(S_x\cup S_y\) 的周期可知 \(d\) 也为 \(S_x\cup S_y\) 的周期,所以它们之间匹配位置一定形成公差为 \(d\) 的等差数列。
\(\text{Theorem 2}\):字符串 \(s\) 所有不小于 \(|s|/2\) 的 \(\rm border\) 构成一个等差数列。
\(\cal Proof\):设 \(|s|-p,|s|-q\) 是 \(2\) 个长度不小于 \(|s|/2\) 的 不同 \(\rm border\) 的长度,且 \(p\) 是 \(s\) 的最小周期。由于 \(|s|-p\ge |s|/2+1,|s|-q\ge |s|/2\),所以 \(p+q\le |s|\). 由引理可得存在一个长度为 \(|s|-\gcd(p,q)\) 的 \(\rm border\),所以 \(\gcd(p,q)=p\). 接下来的情形就和上一条定理一样了。
\(\text{Theorem 3}\):字符串 \(s\) 的所有 \(\rm border\) 按长度排序后,可以被划分成 \(\log |s|\) 个等差数列。
\(\cal Proof\):

考虑先将不小于 \(|s|/2\) 的 \(\rm border\) 组成一个等差数列,接着,令 \(u=s_{1,|s|/2-1},v=s_{|s|-(|s|/2-1)+1,|s|}\),令 \(u\) 的前缀与 \(v\) 的后缀匹配最大值为 \(x\)(这实际上是原串的 \(\rm border\)),显然剩下的 \(\rm border\) 都属于 \(u\cap v\),就又化归到了规模缩小一半的原问题。定理得证。
4. 例题
题目做得还很少,可能会慢慢放上来……
例 1. \(\text{[POI 2005] SZA-Template}\)
多次重复考虑字符串 \(\rm border\). 先建出 \(\rm fail\) 树,答案一定是 \(n\) 到根节点路径上的一点,且答案合法的条件就是相邻两个能放置答案的位置下标差不超过答案的长度。"能放置答案的位置下标" 实际是答案子树的所有点,所以只需要维护子树下标差最大值即可。
从根节点向下爬,最大值是递减的,删除的时候用双向链表维护即可。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号