范畴论玩具:什么是单子 (monad)?
对于上了计概课的同学们, 相信大家都有很多问号, 什么是 monad 捏?
monad 就是自函子范畴上的一个"幺半群" (?)
我们来尝试理解一下这句话在说什么, 首先这里的"幺半群"是在通常意义上的幺半群的一个推广, 也就是说知道什么是幺半群的同学可以先忘掉原有概念
一个范畴 category \(\mathcal C\) 是指下述资料:
- 一些对象, 构成集合 \(\text{Ob}(\mathcal C)\);
- 一些态射, 构成集合 \(\text{Mor}(\mathcal C)\), 以及映射 \(s,t:\text{Mor}(\mathcal C)\to\text{Ob}(\mathcal C)\) 给出态射的来源和目标, 从而对于 \(X,Y\in\text{Ob}(\mathcal C)\), \(\text{Hom}_\mathcal C(X,Y):=s^{-1}(X)\cap t^{-1}(Y)\) 表示 \(X\) 到 \(Y\) 的态射构成的集合, 称为 \(\text{Hom}\)-集;
- 对于 \(X\in\text{Ob}(\mathcal C)\) 都有恒等态射 \(\text{id}_X\in\text{Hom}_\mathcal C(X,X)\);
- 对于 \(X,Y,Z\in\text{Ob}(\mathcal C)\) 都有运算 \(\circ:\text{Hom}_\mathcal C(Y,Z)\times\text{Hom}_\mathcal C(X,Y)\to\text{Hom}_\mathcal C(X,Z)\), 其将 \((f,g)\) 映至 \(f\circ g\), 满足下述性质:
- 对于 \(f,g,h\in\text{Mor}(\mathcal C)\), 若 \((f\circ g)\circ h\) 和 \(f\circ(g\circ h)\) 都有定义, 则 \((f\circ g)\circ h=f\circ(g\circ h)\).
- 对于 \(f\in\text{Hom}_\mathcal C(X,Y)\), 都有 \(f\circ\text{id}_X=\text{id}_Y\circ f=f\).
对象很好理解, 就是一些元素...吗? 大多数时候, 我们应该把对象看作具有某种代数结构的集合, 而态射就是保持这些代数结构的映射.
我们有成堆的数学上的例子, 当然这都不重要, 就看看下面两个:
- 全体集合作为对象构成范畴 \(\textsf{Set}\), 态射及其合成是自明的;
- 对于偏序集 \((P,\le)\), 我们构造范畴 \(\mathcal P\) 如下: 其对象即为 \(P\), 而对 \(x,y\in P\) 若 \(x\le y\) 则存在唯一态射 \(x\to y\), 否则不存在态射. 特别地, 对于 \(n\in\mathbb Z_{\ge 0}\), 将 \(n\) 看作序数等同于全序集 \(\{0,1,\cdots,n-1\}\), 这样构作的范畴记为 \(\bold n\).
虽然但是, 我们好像是学 Haskell 的, 那就来看看这是怎么扯上关系的.
定义范畴 \(\textsf{Hask}\) 的对象是 Haskell 语言的所有类型 a, 态射是所有函数 f :: a -> b, 态射的合成是运算符 (.) :: (b -> c) -> (a -> b) -> a -> c.
接下来就引出描述范畴之间态射的概念, 称为函子 functor, 它们要保持一个范畴所具有的"代数结构", 即对象之间的态射及其合成.
对于范畴 \(\mathcal C',\mathcal C\), 一个函子 \(F:\mathcal C'\to\mathcal C\) 是指下述资料:
- 对象间的映射 \(F:\text{Ob}(\mathcal C')\to\text{Ob}(\mathcal C)\);
- 对于 \(X,Y\in\text{Ob}(\mathcal C')\) 有态射间的映射 \(F:\text{Hom}_\mathcal{C'}(X,Y)\to\text{Hom}_\mathcal C(F(X),F(Y))\) 使得 \(F(f\circ g)=F(f)\circ F(g)\), \(F(\text{id}_X)=\text{id}_{F(X)}\).
对应到 Haskell 语言中, 因为我们现在还只有 \(\textsf{Hask}\) 这个范畴, 所以只能考虑 \(\textsf{Hask}\) 到 \(\textsf{Hask}\) 的函子, 这样的函子称为自函子 endofunctor, 写成代码就是大家熟悉的这个样子:
class Functor f where
fmap :: (a -> b) -> f a -> f b
-- Functor Law #1: fmap id = id
-- Functor Law #2: fmap (f . g) = fmap f . fmap g
这样的 f 称为类型构造器 type constructor, 其将一个类型"包装"为另一个类型, 注意不要与类型 type 搞混了.
有了 Functor 类之后, 在实践过程中我们会遇到 Maybe (Maybe a) 这样的东西, 这启发我们考虑函子的"合成运算", 甚至还有函子之间的态射, 而无聊的 Haskell 设计者们怎么会放过又一次提升抽象层次的机会呢 (?), 即所有自函子构成一个范畴, 称为自函子范畴 endofunctor category, 记作 \(\text{End}(\mathcal C):=\text{Fct}(\mathcal C,\mathcal C)\), 为此我们需要一些准备工作.
对于函子 \(F,G:\mathcal C'\to\mathcal C\), 定义自然变换 natural transformation \(\theta:F\to G\) 是指一族态射 \((\theta_X\in\text{Hom}_\mathcal C(FX,GX))_{X\in\text{Ob}(\mathcal C')}\) 使得下图对 \(\mathcal C'\) 中的态射 \(f:X\to Y\) 交换:
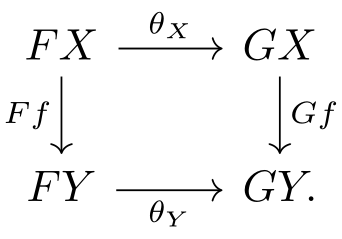
图表交换是指对于起点和终点相同的路径, 其上态射的合成相同, 例如上面的图表就是 \(\theta_Y\circ Ff=Gf\circ\theta_X\).
"自然"在数学上指的是能画出来的图表可交换, 翻译到 Haskell 语言, 实际上是说对于相同的对象构造的函数, 在类型确定的情况下是唯一的, Transformation 类的定义如下:
class (Functor f, Functor g) => Transformation f g t where
(#) :: t -> f a -> g a
-- Natural Law: fmap h . (r #) = (r #) . fmap h
至于函子间合成怎么办捏? 我们要在范畴上定义二元运算, 这引出幺半范畴 monoidal category 的概念. 为了简化理论我们只讨论严格幺半范畴 strict monoidal category, 这是说在范畴 \(\mathcal V\) 上有二元函子 \(\otimes:\mathcal V\times\mathcal V\to\mathcal V\) 和幺元 \(\bold 1\in\mathcal V\) 使得 \((X\otimes Y)\otimes Z=X\otimes(Y\otimes Z)\) 且 \(\bold 1\otimes X=X\otimes\bold 1=X\). 容易验证自函子 \(\text{End}(\mathcal C)\) 构成严格幺半范畴.
严格幺半范畴上的幺半对象 monoid object, 简称 monoid 错误地直译为幺半群是指对象 \(M\) 附带乘法 \(\mu:M\otimes M\to M\) 和幺元 \(\eta:\bold 1\to M\) 满足结合律和幺元性质, 即如下的交换图表:
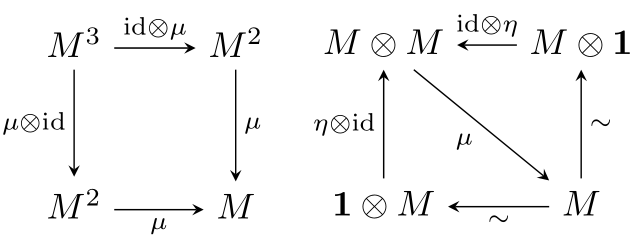
自函子范畴上的幺半对象即为单子 monad. 完成目标, 完结撒花 (?)
先看看远处的错误翻译"幺半群", 实际上不无道理! (哈?)
\(\textsf{Set}\) 作为幺半范畴, 其上的幺半对象确实是通常意义上的幺半群, 因而是一个推广定义!
再重复一遍: 具体到实际意义上时 \(M\) 是函子 (类型构造器) 而 \(\mu\) 和 \(\eta\) 都是自然变换, 而自然变换在定义上是对全体类型 a 的一族态射 (函数).
还是以无聊的 Maybe 举例子, \(\mu\) 称为 join 函数, 将 Maybe (Maybe a) 映至 Maybe a, \(\eta\) 称为 unit 函数, 也记作 pure, return, 将 a 映至 Maybe a, 写成代码就是大家熟悉的这个样子:
class Functor m => Monad m where
return :: a -> m a
join :: m (m a) -> m a
(>>=) :: m a -> (a -> m b) -> m b
-- Monad Law #1 (left identity): join . return = id
-- Monad Law #2 (right identity): join . fmap return = id
-- Monad Law #3 (associativity): join . fmap join = join . join
这里的 (>>=) 是个啥捏? 这就涉及到 monad 在 Haskell 中的具体应用, 例如实现管道操作和 do 语法糖, 与本文讲述理论的主题没啥关系, 而且大家在计概课也有学(
实际上, join 与 (>>=) 可以按照下述方式互相定义:
join :: Monad m => m (m a) -> m a
join x = x >>= id
(>>=) :: Monad m => m a -> (a -> m b) -> m b
x >>= f = join $ fmap f x
相信大家确实理解 monad 是什么了, 于是就真的完结撒花了)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号