issue5:model combination and boosting
model combination其实是和model selection相似的问题,两者都是在模型的选择和评估上做研究。首先说明学习算法:给定训练集D,使用学习算法A在D上学习一个预测规则![]() 。模型选择的目的是,给定这一系列的算法A,如何从中找出一个最好的?评价好坏的标准有两个,一个是可解释性,另一个是效果。显然,两者基本上是成反相关的。简单的模型肯定更加interpretable,但是performance上可能会有问题。
。模型选择的目的是,给定这一系列的算法A,如何从中找出一个最好的?评价好坏的标准有两个,一个是可解释性,另一个是效果。显然,两者基本上是成反相关的。简单的模型肯定更加interpretable,但是performance上可能会有问题。
combination是另一个问题,我们有了这么多模型,能不能从中选取最好的几个,或者是把所有模型使用一种方法组合起来,获得更好的效果呢?事实上,这个问题是有严格的数学证明的。
在PAC(probably approximately correct)的框架下,一个类,如果存在一个多项式的学习算法可以学习它,而且performance很好,那么这个概念成为strongly learnable,反之,如果一个算法performance不那么好,仅仅比50%可能的随机猜测稍好,那么成为weakly learnable。可以证明,strongly learnable与weakly learnable是等价的,即能够存在weakly learnable的类,就一定是strongly learnable。
那么,问题是,给定一组不那么好的算法(模型),能不能把他们提升为一个更好的模型?通过model combination就可以做到这一点。
model combination又称作model ensemble,blending or averaging。
简单的讲,通过等权值投票的方法,就可以将很多模型线性组合起来,形成一个更好的分类器。假设通过不同的模型![]() 生成了一系列预测函数
生成了一系列预测函数![]() ,通过观察组合起来的模型
,通过观察组合起来的模型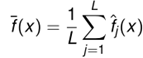 可以得到整体的test err和局部test err之间的关系:
可以得到整体的test err和局部test err之间的关系:
可见,整体模型的错误是比局部错误的平均还低,而多余出来的部分正好是模型多样性(diversity)!那么目标很明确了,为了能使组合之后的模型效果更优,那么需要增加模型之间的多样性。
通常来说,模型选择适用于有一个模型的performance要远超过其他的模型,那么就做模型选择,因为此时如果使用model combination的话,会让最好的效果平均掉。而在很多模型performance都差不多,但是模型之间的差异很大时,适合选择model combination,可以使多样性来增加性能。不同的模型之间结合可以看做一种使模型更加stable的方法。通过前面几节可知,模型越stable,性能就会越好。把多个模型combine到一起,会损失一些interpretation,但是可以更加stable。
在使用主体模型对社团划分时,通常为了使划分的结果更加平滑,所以会使用诸如最近邻的方法进行一个平滑,这就是model combination的思想。
很自然就引出了如何使得模型diversity加强?一般来说,不同的学习方法肯定有效,例如选择SVM和logistic regression以及其他的不同方法。调节模型参数(超参)和使用不同的feature也是不错的选择。还可以使用randomization的方法。
Bagging就是Randomization中的一种,通过把训练集做成几份抽样的结果,可以使用单一的算法训练处具有diversity的模型:
使用有放回抽样的方法,可以从训练数据中,生成很多不同的,但是同样大小不过具有重复样本的很多训练集,使用这些训练集单独训练模型。
boosting也是一种常用的方法,具体会在后续章节中介绍boosting方面的内容。
当然,不同的模型训练结束之后,把这些模型combine起来,不仅只有上述的equally weighted averaging的方法,还有很多其他的办法。exponential weighted averaging是另一种经常被研究的方法,稍稍比equally weighted averaging方法高阶一些:![]() 即把权值改变不同。而权值的计算方法为
即把权值改变不同。而权值的计算方法为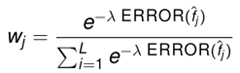 ,忽略掉下面的归一项,这种方法倾向于对较少犯错的模型赋予较大的权值,表明他在combination中起到的作用更重要。容易看出,当lamda=0时,模型退化为equally weighted averaging,当lamda为无穷大的时候,模型变成model selection,倾向于选择performance最佳的模型。 (后续可以参考boosting对model combination的方法)
,忽略掉下面的归一项,这种方法倾向于对较少犯错的模型赋予较大的权值,表明他在combination中起到的作用更重要。容易看出,当lamda=0时,模型退化为equally weighted averaging,当lamda为无穷大的时候,模型变成model selection,倾向于选择performance最佳的模型。 (后续可以参考boosting对model combination的方法)
stacking也是一种常用的model combination的方法。他是上述exponential weighted averaging方法更加general。不同之处在于,参数不是计算出来的,而是通过一种优化算法优化得到的,而优化算法的目标函数就是让combination error达到最小。
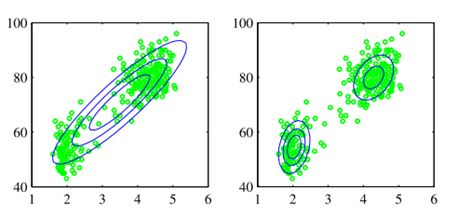
思考: 通常来说,bayesian model averaging要比model combination更进一步。考虑Gaussian Mixtrue Model,GMM假设数据由不同的分布生成,所以需要使用不同的高斯分布拟合每一部分数据,并使用latent variable表示某一段属于哪个Gaussian的概率,通常这个概率服从伯努利分布。可以用一个联合概率表示为![]() ,在观测数据x上的概率分布可以通过求边沿概率获得
,在观测数据x上的概率分布可以通过求边沿概率获得![]() ,在z分布为伯努利,而x在z上的概率分布为高斯的假设下,可以写成
,在z分布为伯努利,而x在z上的概率分布为高斯的假设下,可以写成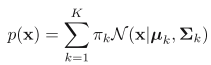 。可见,从intuition上可以看出,每个x都会对应一个z,这表明数据是由不同的分布生成的。这是一个model combination的例子。
。可见,从intuition上可以看出,每个x都会对应一个z,这表明数据是由不同的分布生成的。这是一个model combination的例子。
而bayesian model averaging却假设数据是由单个分布生成的,只不过我们不知道这个分布是什么样子的,他可以是一个高斯分布,或者是混合高斯的,或者是混合其他分布都无所谓,只是我们目前不知道,可能是由于训练集不充分。此时我们有h个不同的模型,每个模型的先验为pr(h)。此时边沿概率分布为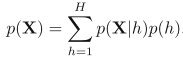 。其中每一个模型都是可以sample所有的数据的,这点和上面不同。pr(h)只不过表示了我们对他到底是什么的不确定性。随着数据的增长,不确定性逐渐降低,最终我们选择了后验概率最大的一个模型。这是model combination和bayesian model averaging的不同之处。
。其中每一个模型都是可以sample所有的数据的,这点和上面不同。pr(h)只不过表示了我们对他到底是什么的不确定性。随着数据的增长,不确定性逐渐降低,最终我们选择了后验概率最大的一个模型。这是model combination和bayesian model averaging的不同之处。

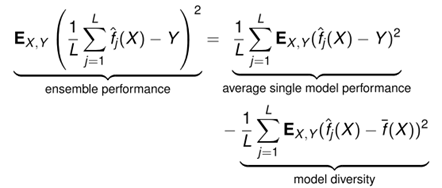



 浙公网安备 33010602011771号
浙公网安备 33010602011771号