issue1：linear regression

线性回归问题是机器学习中的基本问题。线性回归模型解决的是给定输入X，返回Y的过程，这里的Y一般都是连续的变量。

从一般的函数观点来看，线性回归就是找到一个函数，通过观测数据x，可以获得解y，而如此得到的对可以对原始数据拟合的很好。

在统计模型来看，有如下公式：

其中W是参数，b是截距，是噪声。X不是普通意义上的自变量，可以看做由自变量构成的一些特征，视为会更合适。所以线性回归使之参数线性，并非自变量线性。

通常情况下，噪声被认为是期望为0，方差为的高斯分布。即经典的高斯白噪声。（噪声是否可以不是白噪声？）其中期望一定为0，否则的话可以通过加入新的constant特征的方法将噪声中心迁移回原点。

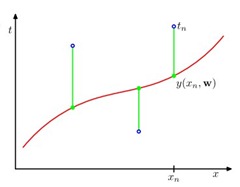
通过最小二乘法（least square）可以实现线性回归的参数求解。直观上看来，如果一条曲线可以让所有的点离该曲线距离（）的差值最小，那么这条曲线一定是表达这些点的最优曲线，有如下公式：

其中是估计值。

这是一个非常简单的凸优化问题，可以使用梯度下降的方法求解，或者直接使用普通二次凸优化的解直接求解。

 

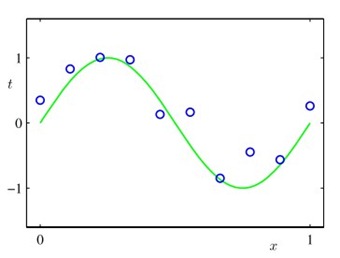
通过最小二乘法和统计模型，可以引出residual的含义。Residual即真实数据减去模型拟合之后滞留的部分。根据统计模型来看，如果滞留的部分是高斯白噪声，那么说明特征的选择是正确的，因为噪声数据是天然存在的，无需拟合。如果residual是有pattern存在的，分布不成噪声形式，那么说明数据中还有没能抽取出来的特征，还需要进一步拟合。

由上可见，通过观察分布的散点图，可以直观进行feature learning。 【待图】

噪声方差估计：

如果噪声的方差是各向同性的，即，则可以通过residual估计其方差。

其中p是特征维度。这种表示是无偏的，而是有偏的。 【待证明】

如果噪声不是各向同性，那么表示不同数据表达整个pattern的能力是不同的。方差越大者，表示其偏离数据中心的可能性更大，方差小者，表示其偏离数据中心点的可能性越小。意即方差较小者比方差较大者更好的fitting原始曲线。在这种情况下，应当对方差小者加大权重，而方差大者调小权重，原始最优化函数变为：

variable importance：

变量重要性衡量了不同的特征feature对回归模型的重要程度。有些变量即使移除，也不会影响整体回归模型的准确度；反之有些变量对模型的准确度有至关重要的影响。具体可以通过假设检验（hypothesis testing）来观察。

【待补充】