快速傅里叶变换（FFT）

引入

现有多项式乘法：

\[(5x^2+3x+7)(7x^2+2x+1) \]

计算时需要暴力展开，得到：

\[35x^4+31x^3+60x^2+17x+7 \]

此时我们一一相乘，时间复杂度为 \(O(n^2)\)。FFT就是一种可以使多项式相乘的时间复杂度降为 \(O(n\log n)\) 的算法。

点值表示

对于一个长度为 \(3\) 多项式 \(5x^2+3x+7\)，我们随便代入一个值作为 \(x\)，那么将得到多项式的值 \(y\)。当我们有 \(4(3+1)\) 个 \((x,y)\)，这些 \((x,y)\) 可以唯一确定这个多项式，这些 \((x,y)\) 就是这个多项式的点值表示。

复数与单位根

复数

复数，即形如 \(a+b\text{ i}\) 的数，其中 \(a\) 为该复数的实数部，\(b\) 为该复数的虚数部，\(\text{i}\) 表示虚数 \(\sqrt{-1}\)。

单位根

单位根，记作 \(w_n^i\)，其几何意义为：

将一个圆心为原点，半径为 \(1\) 的圆等分成 \(n\) 份，每条等分线与圆相交记如下：

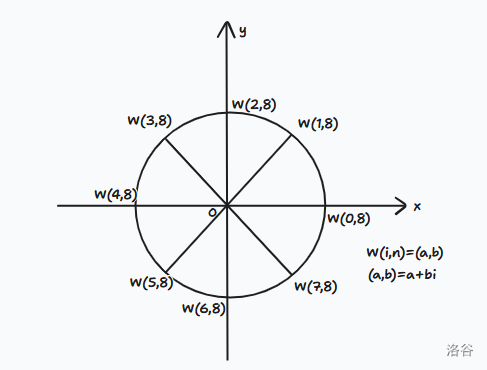
其中 \(w_n^0\) 是该圆与 \(x\) 轴的交点，同时每个单位根 \(w_n^i\) 代表的坐标 \((a,b)\) 表示一个复数 \(a+b\space \text{i}\)。

单位根具有一些性质，例如：

\[w_n^k=w_{2n}^{2k},w_n^{k+\frac{n}{2}}=-w_n^k,w_n^{-k}=\frac{1}{w_n^k} \]

离散傅里叶变化

对于一个长度为 \(n-1\) 的多项式 \(A(x)\)，我们将单位根 \(w_n^0,w_n^1,w_n^2 \cdots w_n^n-1\) 作为 \(x\) 带入 \(A(x)\)。带入后得到的点值表示便是离散傅里叶变化。