菲涅尔反射 Fresnel Reflectance

入射光射到平面上后会被分为反射和折射两个部分，反射向量 $\mathbf{r}_i$ 和入射向量 $\mathbf{l}$ 关于法线 $\mathbf{n}$ 有相同的夹角 $\theta_i$，反射向量 $\mathbf{r}_i$ 可以通过下式得到：

$$\mathbf{r}_i = 2(\mathbf{n}\cdot\mathbf{l})\mathbf{n}-\mathbf{l}$$

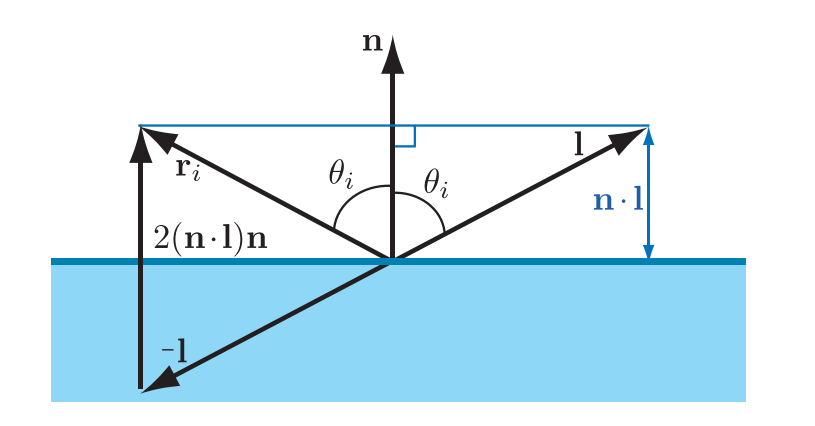
光穿过平面发生的反射和折射遵循菲涅尔方程，菲涅尔方程需要平面遵循几何光学的假设，即平面上不存在大小在$1$至$100$个波长范围内的不规则几何。

反射光占入射光的比例可以通过菲涅尔反射率(Fresnel reflectance) $F$ 描述，菲涅尔反射率和入射角 $\theta_i$ 有关。

光穿过平面时的反射和折射和平面两边物质的折射率有关，我们规定 $n_1$ 表示平面上方(即光照过来的一边)的折射率，$n_2$ 表示平面下方(即发生折射的一边)的折射率。

菲涅尔现象 Fresnel Effect

这种入射角大，反射效果强而清晰，入射角小，反射效果弱而模糊的现象称为菲涅尔现象。

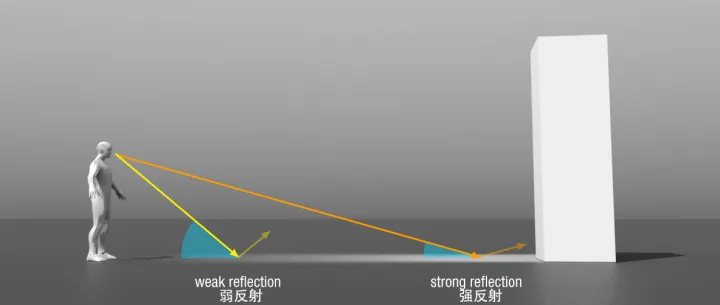
物体的边缘经常会出现菲涅尔现象，因为从物体边缘反射到摄像机的光线入射角较大，如下图：

外反射 External Reflection

当 $n_1<n_2$，即光从折射率较小的一边射到折射率较大的一边时发生的反射我们称为外反射，反之称为内反射。物体外面通常是空气，空气的折射率约是 $1.003$，为了简便，我们认为 $n_1=1$。

对于给定的物质，菲涅尔方程可以被描述成反射率函数 $F(\theta_i)$，虽然该函数在可见光谱上是连续的，但为了方便渲染，可以 be treated as RGB。$F(\theta_i)$ 有如下特征：

• 当 $\theta_i=0^\circ$，即垂直入射时，$F_0$ 可以被认为是该物质的镜面反射颜色；
• 当 $\theta_i$ 逐渐增大时，$F(\theta_i)$ 也逐渐增大，并且对于所有频率的光，当 $\theta_i$ 达到 $90^\circ$ 时，$F(\theta_i)=1$。

如下图是 $F(\theta_i)$ 关于波长和 $\theta_i$ 的可视化，可以看到对于有些物质，该曲线是高度地非线性；该曲线大部分都是单调的，但是对于有些物质（比如铝），该曲线在到达 $1$ 之前会先小幅下降再上升。

我们可以用 $F(\mathbf{n},\mathbf{l})$ 来代替 $F(\theta_i)$，其中 $\theta_i$ 是 $\mathbf{n}$ 和 $\mathbf{l}$ 的夹角。

可以使用一个包含镜面反射颜色 $F_0$ 的式子(Schlick Approximation)来近似菲涅尔反射率：

$$F(\mathbf{n},\mathbf{l}) \approx F_0 + (1 - F_0)(1-(\mathbf{n}\cdot \mathbf{l})^+)^5$$

这玩意其实就是根据入射角的变化对 RGB在 $F_0$ 和白色之间进行插值。

但是 Schlick Approximation 对有些物质的菲涅尔反射率曲线拟合的并不太准，比如下图第二行的铬、铁、锌，实线是真实值，虚线是拟合的结果，但按下方的 color bar 对比其实区别也不算特别明显。

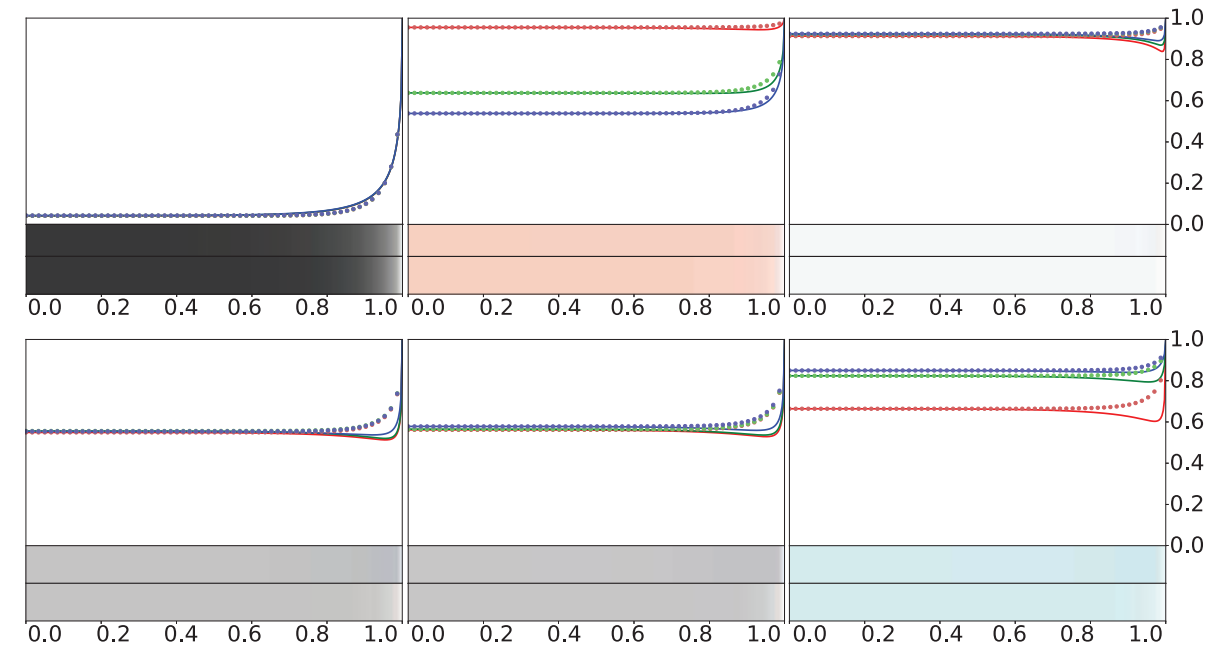
$F_0$ 也可以用折射率来计算，我们令空气的近似折射率 $n_1=1$，然后用 $n$ 代替 $n_2$ 表示物体的折射率，则有

$$F_0 = \left(\frac{n-1}{n+1}\right)^2$$

另一种更通用的近似是

$$F(\mathbf{n},\mathbf{l}) \approx F_0 + (F_{90} - F_0)(1-(\mathbf{n}\cdot \mathbf{l})^+)^5$$

该近似控制了入射角接近 $90^\circ$ 时的菲涅尔反射率，可以用于风格化效果，或是用来处理一些菲涅尔方程不能很好地进行描述的物质。

典型的菲涅尔反射率

物质可以根据它们的光学特性被分为三类：绝缘体(电介质)、导体(金属)、半导体

常见绝缘体的反射率如下，它们反射率 RGB 通道通常没有明显差异，因此给出标量值，对于未知的绝缘体，推荐使用 $0.04$ 作为反射率。

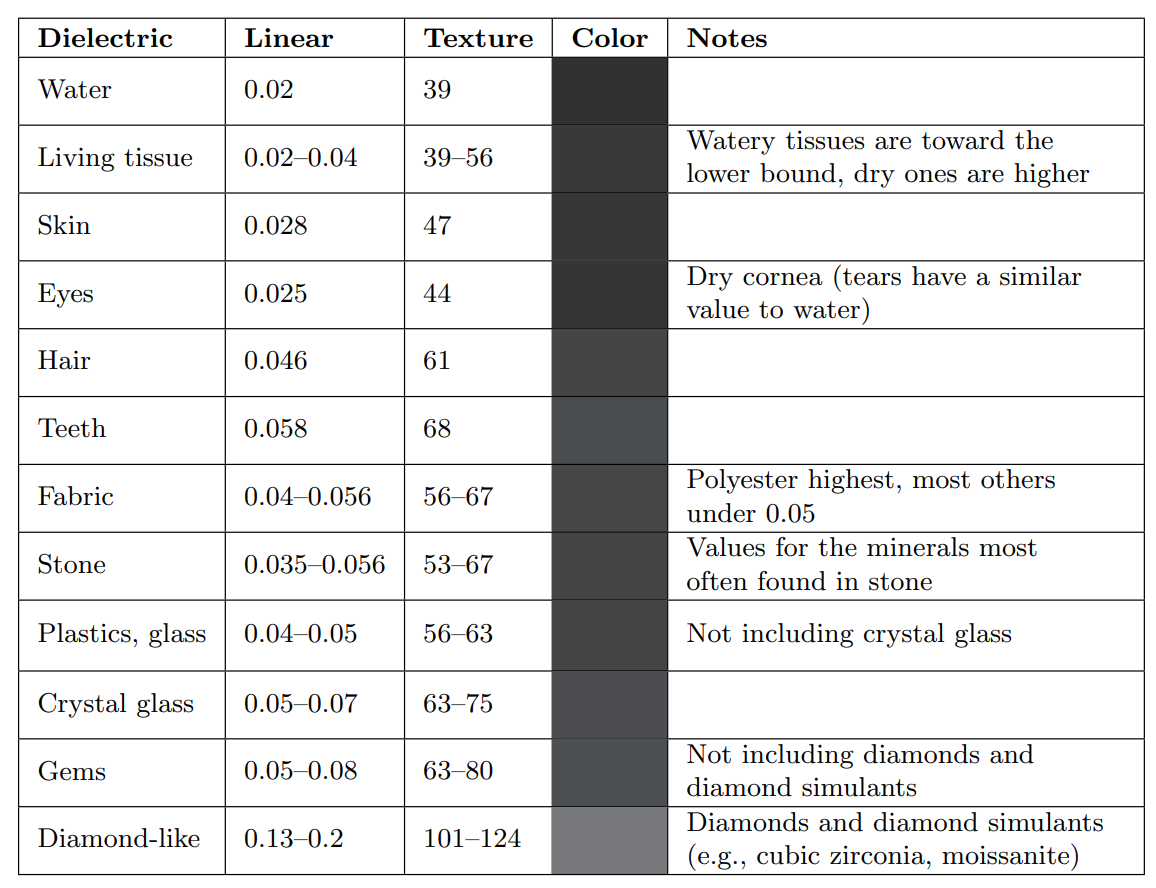
金属的反射率都较大，如下表所示：

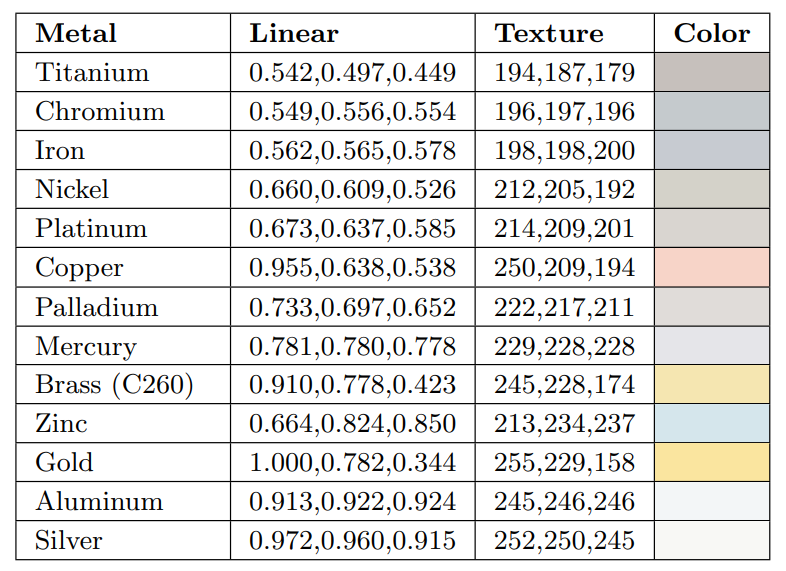
金属会直接吸收掉光，不会表现出次表面散射或透明，因此金属的所有可见颜色都来自 $F_0$。

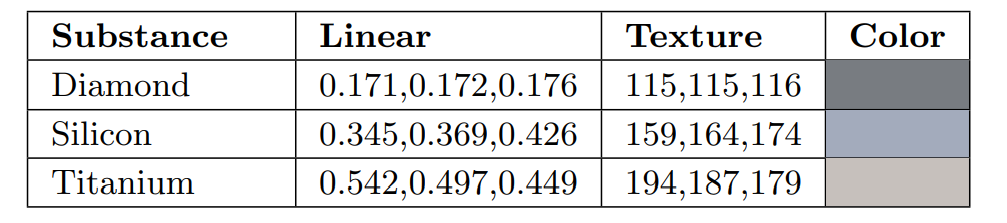
半导体的反射率介于绝缘体和金属之间，如下表所示。半导体在实际的渲染中用到的比较少。

之前我们讨论的外反射发生在空气-物体界面，因此可以认为 $n_1=1$。但如果物体外的介质不是空气，比如放在水中的物体，因为水的折射率 $n_1=1.33$，物质在水中的反射率 $F_0$ 和空气中不太一样：

$$F_0 = \left(\frac{n_1-n_2}{n_1+n_2}\right)^2$$

一些物质在水中和空气中的反射率对比如下，可以发现相比于金属，绝缘体的变化更大

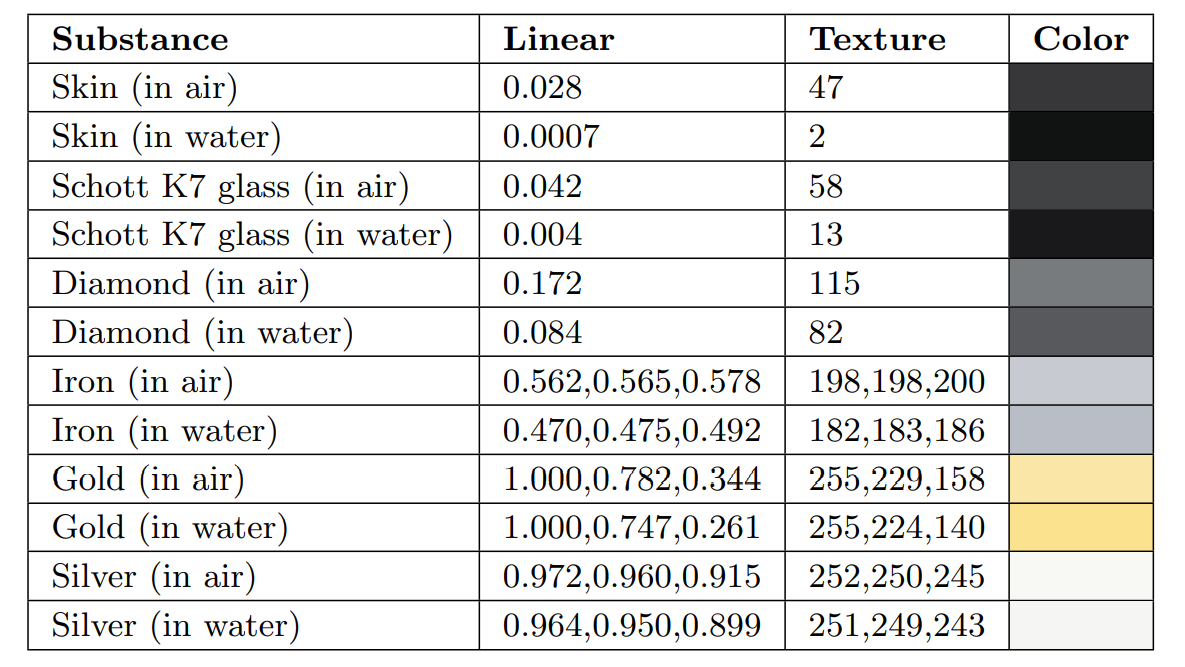
内反射 Internal Reflection

内反射发生在 $n_1>n_2$ 的时候，即光线从物体内部射到界面上的时候。

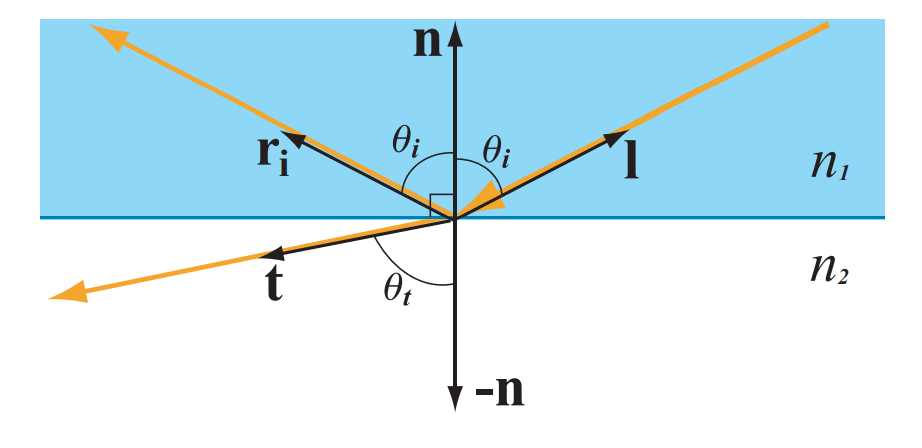
斯涅尔定律：

$$\sin(\theta_t) = \frac{n_1}{n_2} \sin(\theta_i)$$

其中 $\theta_t$ 是折射角。

当 $n_1>n_2$ 时，容易发现，当 $\sin(\theta_i)$ 还没到达 $1$ 时， $\sin(\theta_t)$ 就可能到达 $1$，此时 $\theta_i$ 再增大，将不会发生折射现象，入射光全部反射出去，此现象称为全反射。

因为菲涅尔方程是对称的，入射矢量和折射矢量可以互换。再根据斯涅尔定律，我们可以知道内反射的反射率曲线相比于外反射将会被压缩，并且 $\theta_i$ 达到临界角 $\theta_c$ 时反射率达到 $1$，发生全反射：

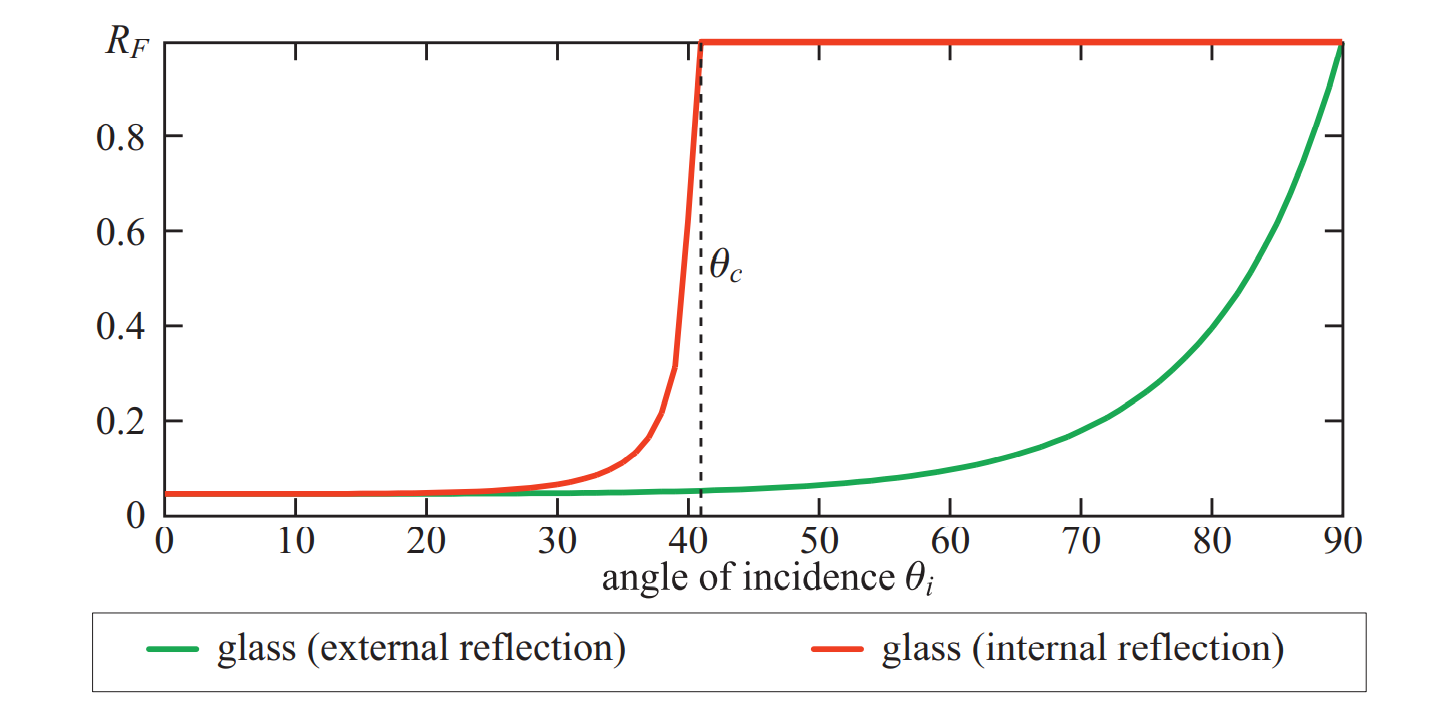
内反射只在绝缘体中出现，因为金属和半导体将迅速吸收在其内部传输的光。而绝缘体有实值折射率，因此全反射临界角 $\theta_c$ 可以由下式计算：

$$\sin(\theta_c) = \frac{1-\sqrt{F_0}}{1+\sqrt{F_0}}$$

推导过程如下：

$$1=\sin(\theta_t) = \frac{n_1}{n_2}\sin(\theta_c)\\ \sin(\theta_c) = \frac{n_2}{n_1}\\ F_0 = \left(\frac{n_1-n_2}{n_1+n_2}\right)^2\\ \sqrt{F_0} = \frac{n_1-n_2}{n_1+n_2}\\ (n_1+n_2)\sqrt{F_0}=n_1-n_2\\ \left(1+\frac{n_2}{n_1}\right)\sqrt{F_0} = 1 - \frac{n_2}{n_1}\\ \sin(\theta_c) = \frac{1-\sqrt{F_0}}{1+\sqrt{F_0}}$$