位运算(2)Amr and Chemistry
Amr and Chemistry
time limit per test1 second
Amr loves Chemistry, and specially doing experiments. He is preparing for a new interesting experiment.
Amr has n different types of chemicals. Each chemical i has an initial volume of ai liters. For this experiment, Amr has to mix all the chemicals together, but all the chemicals volumes must be equal first. So his task is to make all the chemicals volumes equal.
To do this, Amr can do two different kind of operations.
- Choose some chemical i and double its current volume so the new volume will be 2ai
- Choose some chemical i and divide its volume by two (integer division) so the new volume will be ai/2
![]()
Suppose that each chemical is contained in a vessel of infinite volume. Now Amr wonders what is the minimum number of operations required to make all the chemicals volumes equal?
Input
The first line contains one number n (1 ≤ n ≤ 105), the number of chemicals.
The second line contains n space separated integers ai (1 ≤ ai ≤ 105), representing the initial volume of the i-th chemical in liters.
Output
Output one integer the minimum number of operations required to make all the chemicals volumes equal.
input
3
4 8 2
output
2
input
3
3 5 6
output
5
Note
In the first sample test, the optimal solution is to divide the second chemical volume by two, and multiply the third chemical volume by two to make all the volumes equal 4.
In the second sample test, the optimal solution is to divide the first chemical volume by two, and divide the second and the third chemical volumes by two twice to make all the volumes equal 1.
1e5 * (1/2)^7 < 1; 所以 可以枚举每一个数的所有可以到达的位置,用vis[]记录该点出现次数,最后判断vis[] = n的,再比较step[]大小就ok了!
#include<cstdio> #include<algorithm> const int maxn = 1e5+5; using namespace std; int a[maxn]; int vis[maxn]; int step[maxn*2]; int main(){ int n; scanf("%d",&n); for(int i = 0; i < n; i++){ scanf("%d",&a[i]); int temp = a[i]; int step1 = 0,step2 = 0,step3 = 0; while(temp < maxn){ step1++; vis[temp]++; temp = temp<<1; step[temp] += step1; } while(a[i] >= 1){ if(a[i] & 1 && a[i]!=1){ int temp1 = a[i] = a[i] >> 1; step2++; step3 = step2; vis[a[i]]++; step[a[i]] += step3; while(temp1 < maxn){ step3++; temp1 = temp1<<1; vis[temp1]++; step[temp1] += step3; } } else { step2++; a[i] = a[i] >> 1; vis[a[i]]++; step[a[i]] += step2; } } } int ans = 1e9; for(int i = 1; i < maxn; i++){ if(vis[i] == n){ ans = min(step[i],ans); } } printf("%d\n",ans); return 0; }



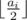

 浙公网安备 33010602011771号
浙公网安备 33010602011771号