498C Array and Operations (二分图最大匹配or最大流)
You have written on a piece of paper an array of n positive integers a[1], a[2], ..., a[n] and m good pairs of integers (i1, j1), (i2, j2), ..., (im, jm). Each good pair (ik, jk) meets the following conditions: ik + jk is an odd number and 1 ≤ ik < jk ≤ n.
In one operation you can perform a sequence of actions:
- take one of the good pairs (ik, jk) and some integer v (v > 1), which divides both numbers a[ik] and a[jk];
- divide both numbers by v, i. e. perform the assignments:
![]() and
and ![]() .
.
Determine the maximum number of operations you can sequentially perform on the given array. Note that one pair may be used several times in the described operations.
The first line contains two space-separated integers n, m (2 ≤ n ≤ 100, 1 ≤ m ≤ 100).
The second line contains n space-separated integers a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 109) — the description of the array.
The following m lines contain the description of good pairs. The k-th line contains two space-separated integers ik, jk (1 ≤ ik < jk ≤ n,ik + jk is an odd number).
It is guaranteed that all the good pairs are distinct.
Output the answer for the problem.
3 2
8 3 8
1 2
2 3
0
3 2
8 12 8
1 2
2 3
2
传送门: http://codeforces.com/problemset/problem/498/C
题意:给你整数a[1]~a[n],再给你m对序号,每对的序号和总是奇数,每次的操作:可以随便挑一对序号 ( i , j ) ,随便找个整数v同时分别去除a[i]和a[j], a[i],a[j]数值改变(要整除),问你这样的操作你最多能弄几次。
思路:首先要保证操作次数最大,每次除的时候都应该除质数,下标之和为奇数,不难发现它构成了一张二分图。于是我们可以枚举每个a[i]的质数,然后建立对应的图,跑网络流最大流即可。也就是枚举a[i]中存在的质数,将源点source与 a[奇数](可以被这个质数整除)相连,流量为存在这个质数的个数,汇点与a[偶数]相连,流量同理,最后将m对中的奇数偶数点相连,流量为inf,最后跑最大流。
当然这道题可以将a[奇数],a[偶数]中的质数都分别一个个全拆出来, (比如12就拆成2,2,3) 将m对中的a[奇数],a[偶数]点中有相同质数都相连,跑个最大二分图匹配就OK。
代码:最大流

#include <vector>
#include <memory.h>
#include <map>
#include <algorithm>
using namespace std;
const int MAXN = 110;
const int INF = 1000000000;
int vcnt, a[MAXN], u[MAXN], vt[MAXN];
bool marked[MAXN];
int cap[MAXN][MAXN];
vector<int> v;
map<int, int> cnt[MAXN];
int dfs(int v, int sink, int lim)
{
if (v == sink)
return lim;
if (marked[v])
return 0;
marked[v] = true;
for (int i = 0; i < vcnt; i++)
if (cap[v][i])
{
int x = dfs(i, sink, min(cap[v][i], lim));
if (x)
{
cap[v][i] -= x;
cap[i][v] += x;
return x;
}
}
return 0;
}
int maxFlow(int source, int sink)
{
int x;
int ans = 0;
do
{
memset(marked, false, sizeof marked);
x = dfs(source, sink, INF);
ans += x;
}
while (x);
return ans;
}
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
int tmp = a[i];
for (long long j = 2; j * j <= tmp; j++)
while (tmp % j == 0)
{
cnt[i][j]++;
tmp /= j;
v.push_back(j);
}
if (tmp > 1)
{
cnt[i][tmp]++;
v.push_back(tmp);
}
}
for (int i = 0; i < m; i++)
{
cin >> u[i] >> vt[i];
if (vt[i]%2 == 1)
swap(u[i], vt[i]);
}
sort(v.begin(), v.end());
v.resize(unique(v.begin(), v.end()) - v.begin());
int sink = n+1, source = n + 2, ans = 0;
vcnt = n + 3;
for (int j = 0; j < v.size(); j++)
{
memset(cap, 0, sizeof cap);
for (int i = 0; i < m; i++)
cap[u[i]][vt[i]] = INF;
for (int i = 1; i <= n; i++)
if (i % 2 == 1)
cap[source][i] = cnt[i][v[j]];
else
cap[i][sink] = cnt[i][v[j]];
ans += maxFlow(source, sink);
}
cout << ans << endl;
}
代码:最大二分匹配

#include <cstring>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
vector<pair<int,int> > fac[200];
int N, M, cnt,ent,A[200];
const int MAXN = 1000000;//点数的最大值
const int MAXM = 1000000;//边数的最大值
struct Edge
{
int to,next;
} edge[MAXM];
int head[MAXN],tot;
void init()
{
tot = 0;
memset(head,-1,sizeof(head));
}
void addedge(int u,int v)
{
edge[tot].to = v;
edge[tot].next = head[u];
head[u] = tot++;
}
int linker[MAXN];
bool used[MAXN];
int uN;
bool dfs(int u)
{
for(int i = head[u]; i != -1 ; i = edge[i].next)
{
int v = edge[i].to;
if(!used[v])
{
used[v] = true;
if(linker[v] == -1 || dfs(linker[v]))
{
linker[v] = u;
return true;
}
}
}
return false;
}
int hungary()
{
int res = 0;
memset(linker,-1,sizeof(linker));
for(int u = 0; u < uN; u++) //点的编号0~uN-1
{
memset(used,false,sizeof(used));
if(dfs(u))res++;
}
return res;
}
int main()
{
init();
scanf("%d %d", &N, &M);
for(int Ni = 1; Ni <= N; Ni++)
{
scanf("%d", &A[Ni]);
int x = A[Ni];
for(int i = 2; i*i <= x; i++)
while( x%i == 0 )
{
x /= i;
fac[Ni].push_back(make_pair(i, Ni%2==1? cnt++:ent++));
}
if(x != 1) fac[Ni].push_back(make_pair(x, Ni%2==1? cnt++:ent++));
}
for(int Mi = 1; Mi <= M; Mi++)
{
int a, b;
scanf("%d %d", &a, &b);
if(b%2 == 1)
swap(a,b);
for(int i = 0; i < fac[a].size(); i++)
for(int j = 0; j < fac[b].size(); j++)
if( fac[a][i].first == fac[b][j].first)
{
addedge(fac[a][i].second,cnt+fac[b][j].second);
}
}
uN=cnt;
printf("%d\n", hungary());
}





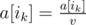
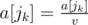 .
.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号