【DSP】 01 简介&离散系统概述

写这个文档大概是为了以后复习时用以及供未来查阅
文档内容不保证全部正确，如有错误和缺失大概是我上课睡着了……
文档内容主要是一些听课的笔记，目前未进行总结归纳之类（大概就是笔记ppt照搬）

现实中信号往往是连续的或者说是模拟的，但是在实际的通信系统中，几乎都是采用离散时间信号。

1. 离散信号概述

现代的信号处理系统往往会通过ADC进行采样，将模拟信号转换为数字信号后进行数字信号处理，这样做的原因主要是DSP技术成本低、效果好。

信号的分类

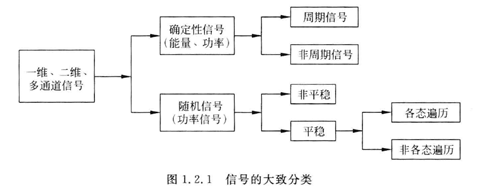
2. 信号空间

2.1. 赋范线性空间

Def: 范数：从不同的角度测量信号的某个特征量

\[\begin{align} \tag{1.1}||x||_\infty&=\max\{|x(n)|:-\infty<n<\infty\}\\ \tag{1.2}||x||_1&=\sum_{-\infty}^\infty|x(n)|\\ \tag{1.3}||x||_2&=\sqrt{\sum_{n=-\infty}^{+\infty}|x(n)|^2} \end{align} \]

显然 \(||x||_{\infty}\) 表示了信号的最大幅度，\(||x||_1\)表示了信号的绝对和，\(||x||_2\)表示了信号的能量。
对于上述的三个信号，我们可以定义三种空间：

\[\begin{align} \tag{1.4}L_\infty&=\{x:||x||_{\infty}<\infty\}\\ \tag{1.5}L_1&=\{x:||x||_{1}<\infty\}\\ \tag{1.6}L_2&=\{x:||x||_{2}<\infty\} \end{align} \]

\(L_\infty\)定义的空间表示幅度有界的信号的集和，\(L_2\)表示能量有界的信号的集和，上述三种空间都是线性空间，而定义了范数的线性空间又称为赋范线性空间。

那么为何要定义赋范线性空间？
TBD

为何要定义范数？

为了描述“大小”的概念

如果要定义一个范数必须满足下面3个条件

非负性：\(||x||\geq0\)，且只有\(x\)为全0信号时，才能取到0；
线性：\(||\lambda x||=|\lambda|\times||x||\)，\(\lambda\in\mathbb{R}\)
满足三角不等式：\(||x+y||\leq||x||+||y||\)

2.2. 度量空间

如何定义两个信号的“距离”：

\[\tag{2.1}d(x,y)=||x(n)-y(n)||_2 \]

定义的距离需要满足如下的性质：

非负性：\(0\leq d(x,y)<\infty\)，且当且仅当\(x(t),y(t)\)处处相等时or信号\(y(t)\)在均方意义上收敛于\(x(t)\)时才取等号。
互易性：\(d(x,y)=d(y,x)\)
三角不等式：\(d(x,y)\leq d(x,z)+d(z,y)\)
定义了距离的空间被称作度量空间，显然赋范线性向量空间是度量空间。

为何要定义距离
TBD

✨内积空间

定义内积：

\[\tag{2.2}\langle x,y \rangle=\sum_{n=-\infty}^{+\infty}x(n)y^*(n) \]

若要定义内积必须满足以下性质：

\[\tag{2.3}\langle x,y\rangle\times\\ \langle \alpha x+\beta y,z\rangle=\alpha\langle x,z\rangle+\beta\langle y,z\rangle\\ \langle x,x\rangle\geq0\]

信号距离及范数的关系

\[\tag{2.4}\begin{aligned} d^{2}(x, y) &=\int_{a}^{b}[x(t)-y(t)][x(t)-y(t)]^{*} \mathrm{d} t \\ &=\|x\|_{2}^{2}+\|\boldsymbol{y}\|_{2}^{2}-2 \operatorname{Re}\langle \boldsymbol{x}, \boldsymbol{y}\rangle \end{aligned}\]

3.离散时间系统的基本概念

一个离散时间系统，可以抽象为一种变换，或是一种映射，即把输入序列：\(x(n)\)变换为输出序列\(y(n)\)

对于离散时间系统的描述：

差分方程，卷积（convolution）关系
转移函数（Z 变换）, 频率响应（DTFT, DFT）

FIR&IIR

有限冲激响应（finite impulse response， FIR)系统，简称为 FIR 系统。一阶自回归模型中由于包含了由输出到输入的反馈， 因此其抽样响应为无限长，我们称这一类系统为 “ 无限冲激响应”（infinite impulse response， IIR)系统，简称为IIR 系统。

离散时间系统的性质

线性

线性的含义是指该系统的输入、输出之间满足叠加原理

移不变性

设一个离散时间系统对\(x(n)\)的响应是\(y(n)\) ，如果将\(x(n)\)延迟了\(k\)个抽样周期，输出\(y(n)\)也相应地延迟了\(k\)个抽样周期，那么，我们说该系统具有移不变性，即

\[T[x(n-k)]=y(n-k) \]

该性质的含义还可直观地解释为：对给定的输入，系统的输出和输人施加的时间无关。即不论何时加上输入，只要输入信号一样，输出信号的形态就保持不变。

因果性

一个 LSI 系统，如果它在任意时刻，例如的输出只决定于现在时刻和过去的输人，而和将来的输人无关，那么，我们说该系统是因果（causal )系统，

稳定性

一个信号\(x(n)\)，如果存在一个实数\(R\)，使得对所有的n都满足\(|x(n)|\leq R\)，那么，我们称是有界的。对一个LSI系统，若输入\(x(n)\)是有界的，输出：\(y(n)\)也有界， 那么该系统是稳定 (stable)的。

系统稳定性判据 1

\[\sum_{n=-\infty}^{\infty}|h(n)|<\infty \]

🎶线性卷积

信号通过一个系统，可以用卷积的形式表示

\[\tag{3.1}y(n)=\sum_{k=-\infty}^{\infty}x(k)h(n-k) \]

\[\tag{3.1}y(n)=\sum_{k=-\infty}^\infty h(k)x(n-k) \]

矩阵型式

若\(x(n)\)是一个\(N\)点的序列，\(h(n)\) 是一个 \(M\) 点的序列，那么卷积的结果\(y(n)\)幻将是 \(L=N+M-1\)点的序列。其矩阵表示形式入式\((3.3)\)

\[\tag{3.3} \left[ \begin{matrix} y(0)\\ y(1)\\ \vdots\\ y(M-1)\\ \vdots\\ y(N-1)\\ \vdots\\ y(L) \end{matrix} \right]=\left[ \begin{matrix} x(0)&\quad&\quad&\dots&\quad\\ x(1)&x(0)&\quad&\dots&0\\ x(2)&x(1)&x(0)&0&\dots\\ x(M-1)&\dots&\quad&\quad&x(0)\\ \vdots&\ddots&\dots&\quad&\vdots\\ 0&\quad&\quad&\quad&\quad\\ \quad&\quad&\quad&\quad&x(N-1) \end{matrix} \right] \left[ \begin{matrix} h(0)\\ h(1)\\ \vdots\\ h(M-1) \end{matrix} \right] \]

系统的频率响应

系统的频率响应，又称系统的特征值。上式实际上是离散序列的傅里叶变换(discrete time Fourier transform, DTFT)

\[\tag{3.4}H(e^{j\omega})=\sum_{n=-\infty}^{\infty}h(n)e^{-j\omega n} \]

幅度响应与相位响应

\[\begin{array}{l} \left|H\left(\mathrm{e}^{\mathrm{j} \omega}\right)\right|=\left[H_{\mathrm{R}}^{2}\left(\mathrm{e}^{\mathrm{i} \omega}\right)+H_{1}^{2}\left(\mathrm{e}^{\mathrm{j} \omega}\right)\right]^{1 / 2} \\ \varphi(\omega)=\arctan \frac{H_{1}\left(\mathrm{e}^{\mathrm{j} \omega}\right)}{H_{\mathrm{R}}\left(\mathrm{e}^{\mathrm{j} \omega}\right)} \end{array}\]

奇偶特性？

转移函数

\[H(z)=\sum_{n=-\infty}^{\infty}h(n)z^{-n} \]

Summary

离散系统的研究主要包括两方面的内容，一是系统的分析，二是系统的综合。
系统的分析是指，** 给定了一个系统(可能是\(h(n)\)，或\(H(e^{j\omega})\)，或 \(H(z)\)，或一个差分方程，或一个信号流图**，或是在给定输入下的输出) 后，如何去了解该系统的特性。这些特性包括系统的线性、移不变性、物理可实现性及稳定性，还包括频率特性（是低通、高通、带通还是带阻）、相位特性（相位是否具有线性相位，是否具有最小相位）。

晴耕雨读