20202317 2021-2022-1 《图》实验九报告
# 20202317 2021-2022-1 《图》实验九报告
课程:《程序设计与数据结构》
班级: 2023
姓名: 向岩杰
学号:20202317
实验教师:王志强
实验日期:2021年12月19日
必修/选修: 必修
实验内容:
(1) 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
(2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
(3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)
实验过程及结果
(1) 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)





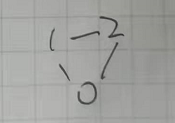
(2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
无向图:
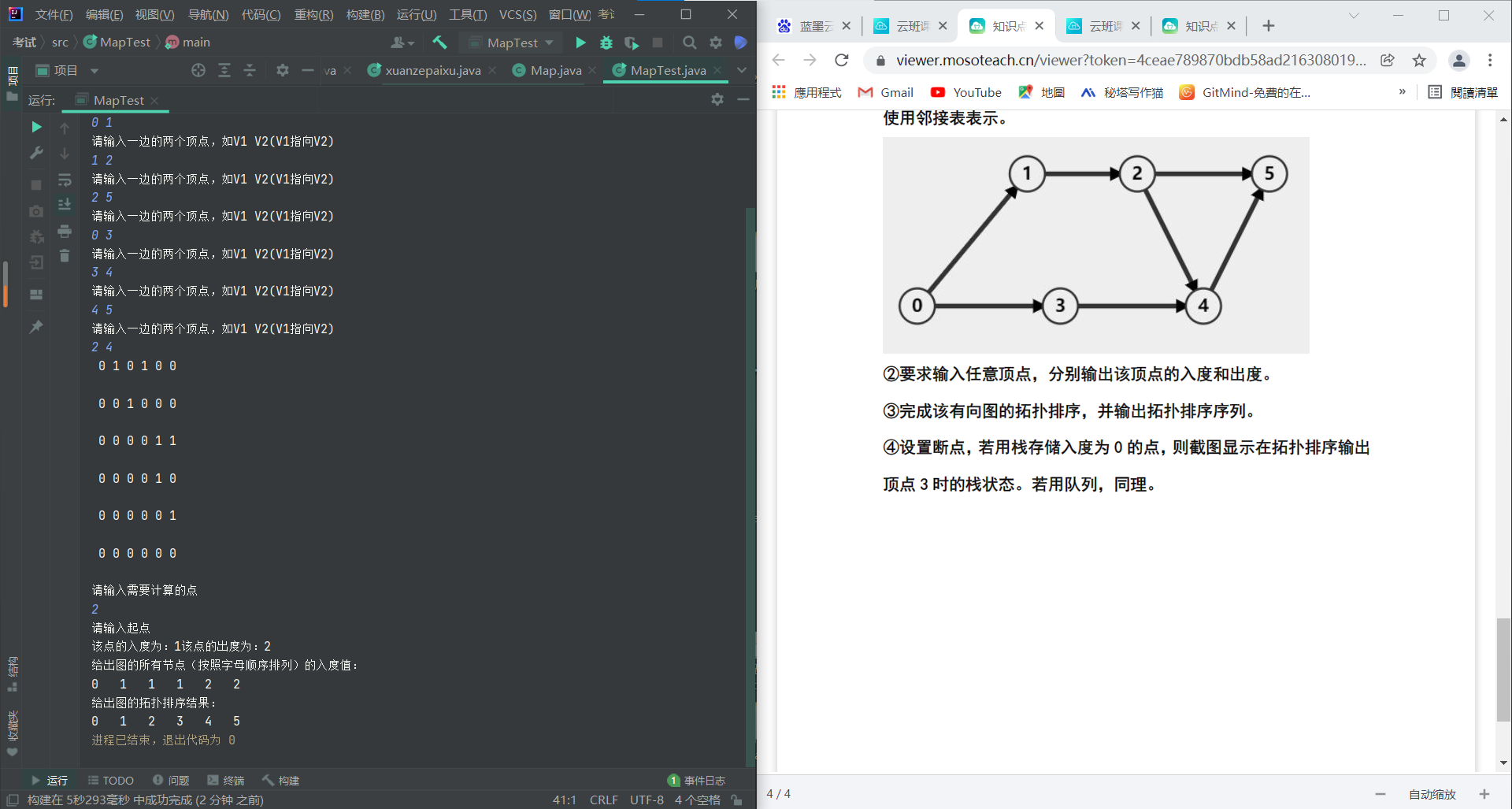
(3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
import java.util.Scanner;
public class MapTest {
public int[] getSourceSort(int[][] adjMatrix,int[] source){
int len = source.length;
int[] result = new int[len];
int count = 0;
boolean judge = true;
while(judge){
for(int i = 0;i < source.length;i++){
if(source[i] == 0){
result[count++] = (0+i);
source[i] = -1;
for(int j = 0;j < adjMatrix[0].length;j++){
if(adjMatrix[i][j] == 1)
source[j] -= 1;
}
}
}
if(count == len)
judge = false;
}
return result;
}
public int[] getSource(int[][] adjMatrix){
int len = adjMatrix[0].length;
int[] source = new int[len];
for(int i = 0;i < len;i++){
int count = 0;
for(int j = 0;j < len;j++){
if(adjMatrix[j][i] == 1)
count++;
}
source[i] = count;
}
return source;
}
public static void main(String[] args) {
int v = 0;
int e;
int[][] adjacencymatrix = new int[256][256];
Scanner scan = new Scanner(System.in);
Map xyjMap = null;
System.out.println("请输入顶点数");
v = scan.nextInt();
System.out.println("请输入边数");
e = scan.nextInt();
adjacencymatrix = new int[v][v];
xyjMap = new Map(adjacencymatrix,v,e);
xyjMap.createDgMap(adjacencymatrix, v, e);
System.out.println("请输入需要计算的点");
int begin;
begin = scan.nextInt();
xyjMap.inOrout(adjacencymatrix,begin,v);
MapTest test = new MapTest();
int[] source = test.getSource(adjacencymatrix);
System.out.println("给出图的所有节点(按照字母顺序排列)的入度值:");
for(int i = 0;i < source.length;i++)
System.out.print(source[i]+"\t");
System.out.println();
int[] result = test.getSourceSort(adjacencymatrix, source);
System.out.println("给出图的拓扑排序结果:");
for(int i = 0;i < result.length;i++)
System.out.print(result[i]+"\t");
}
}
(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
import java.util.*;
import java.io.*;
class S //栈类,先进后出
{
private final int SIZE = 20; //栈的大小是20
private int[] st; //栈内存储的是int类型的数字
private int top; //栈的头指针
public S() //构造方法
{
st = new int[SIZE];
top = -1; //注意,初始的时候,top指针指的是-1
}
public void push(int j) //向栈内送入元素
{
st[++top] = j;
}
public int pop() //栈内弹出栈顶元素
{
return st[top--];
}
public int peek() //显示栈顶元素
{
return st[top];
}
public boolean isEmpty() //判断栈是否为空
{
return (top == -1);
}
}
class Vertex //图中用此类来表示一个顶点
{
public char label;
public boolean wasVisited;
public Vertex(char lab)
{
label = lab;
wasVisited = false;
}
}
class G
{
private final int MAX_VERTS = 20;
private Vertex[] vertexList;
private int adjMat[][]; //邻接矩阵
private int nVerts;
//private char sortedArray[];
private S theStack; //栈,用来存储每一个图的节点
public G()
{
vertexList = new Vertex[MAX_VERTS]; //数组
adjMat = new int[MAX_VERTS][MAX_VERTS]; //二维数组模拟邻接矩阵
nVerts = 0;
for(int i = 0; i < MAX_VERTS; i++) //初始化邻接矩阵
{
for(int j = 0; j < MAX_VERTS; j++)
{
adjMat[i][j] = 0;
}
//sortedArray = new char[MAX_VERTS];
}
theStack = new S();
}
public void addVertex(char lab) //无向图插入一个顶点
{
vertexList[nVerts++] = new Vertex(lab);
}
public void addEdge(int start,int end) //无向图插入一条边,注意是无向图,所以两边都要插入
{
adjMat[start][end] = 1;
adjMat[end][start] = 1;
}
public void displayVertex(int v) //显示无向图
{
System.out.print(vertexList[v].label);
}
public int getAdjUnvisitedVertex(int v)
{
for(int i = 0; i < nVerts; i++)
if(adjMat[v][i] == 1 && vertexList[i].wasVisited == false) //某一个顶点有邻接节点并且是未访问过的
return i;
return -1;
}
public void mst() //用DFS来模拟最小生成树
{
vertexList[0].wasVisited = true;
theStack.push(0);
while(! theStack.isEmpty())
{
int currentVertex = theStack.peek();
int v = getAdjUnvisitedVertex(currentVertex);
if(v == -1)
theStack.pop();
else
{
vertexList[v].wasVisited = true;
theStack.push(v);
displayVertex(currentVertex);
displayVertex(v);
System.out.print(" ");
}
}
for(int j = 0; j < nVerts; j++) //最后,当栈内的所有节点都为空时,则将节点矩阵置为已访问过
vertexList[j].wasVisited = false;
}


(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)



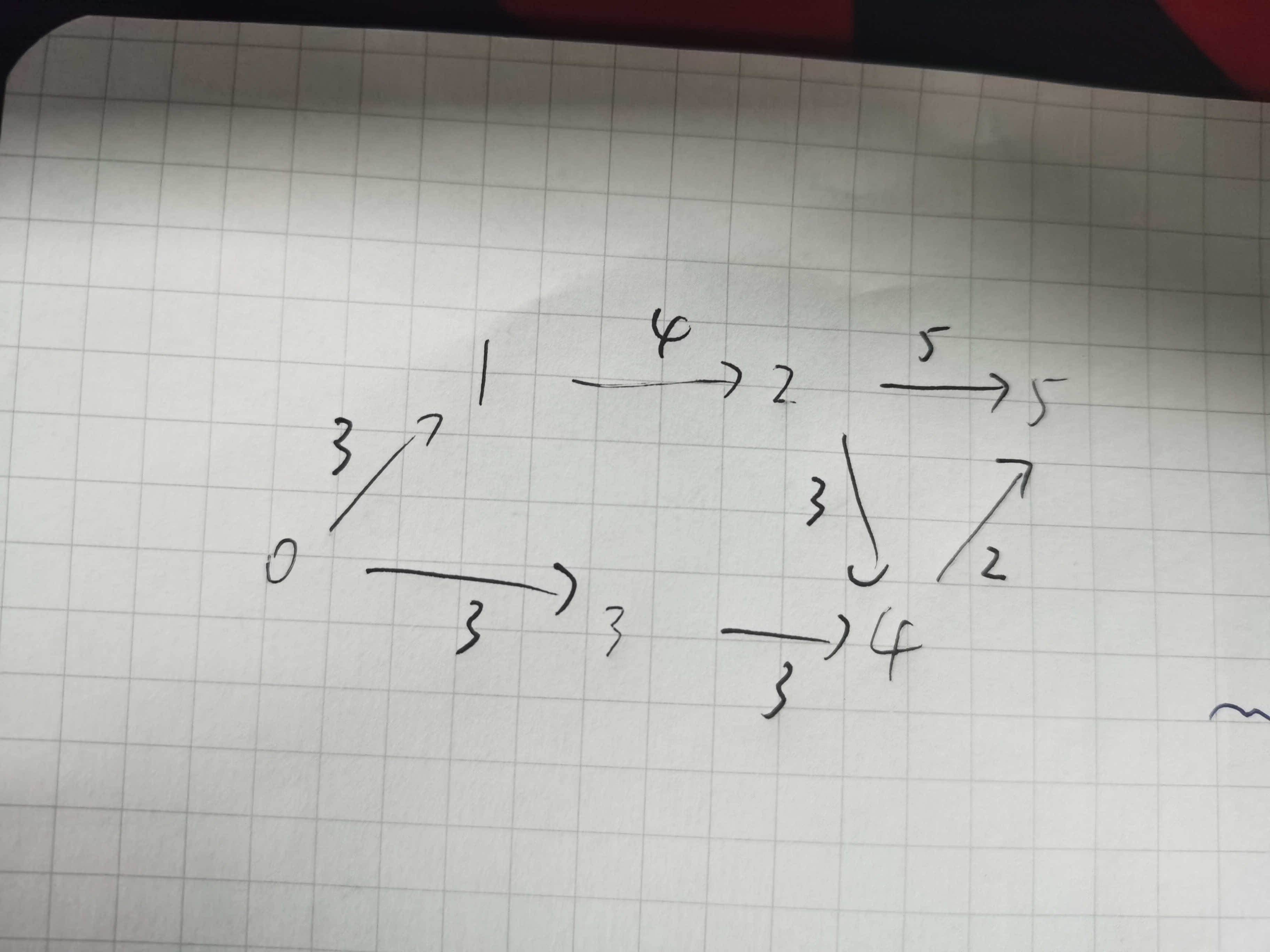
三. 实验过程中遇到的问题和解决过程
问题1:关于在递归时栈溢出和数组溢出的问题
解决方式:特别是遍历的时候,数组溢出的问题时有发生,主要是由于用来计数的变量在遇到需要回溯的地方时计数的变量不好选择,理清楚逻辑就好了
问题2:在遍历时由于是用的纯二维数组导致后续的递归逻辑不好控制
解决办法:硬写。。。效果不好,下次一定用邻接表
四、感悟
这次的实验比较不顺利,主要是被遍历拦住了,感觉我的代码还有很大问题和优化的地方。特别是如何回溯这一点还有待改善。加油



