归纳和递归
完全归纳
令依据情况为S（i0）,s(i0+1),…s(j0),并根据已经证明了对任意的n≥j0，S（i0）,S(i0+1),…，S（n）能一起推出S（n+1）。现在，假设至少存在一个不小于i0的n值使S（n）不成立，并设b是令S（b）为假的最小的不小于i0的整数。那么b就不能是i0和j0之间的整数，否则与归纳依据矛盾。此外b也不能大于j0。不然S（i0）,S(i0+1),…，S（b-1）全为真。而归纳步骤接着就回告诉我们S(b)也为真，这样就产生了矛盾。
现在探讨将算术表达式变形为等价形式的例子。它表明完全归纳利用了可假设待证明的命题S对所有n以下（包含n）的参数都为真这一事实。
作为一种激励形式，编程语言的编译器可以利用算术运算符的代数形式，重新排列所计算的算术表达式中操作数的顺序。这种重排的目标是为计算机找出一种比表达式原有计算顺序耗时更少的方式来计算该表达式。
现在，只考虑含有一种结合和交换运算符（比如+）的算术表达式，并看看可以对操作数进行怎样的重新排列。我们将证明，如果有任意只含“+”运算符的表达式，那么该表达式的值，要与其他任何只对同样操作数使用“+”的表达式的值相等，不管以何种顺序排列及（或）以何种形式组合。例如
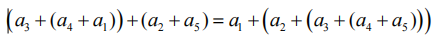
归纳：设E有 n +1个操作数，并假设S(i)对i = 2 , 3, …, n都为真。我们需要为 n≥ 2 证明该归纳步骤，所以可假设E最少有3个操作数，也就是至少出现两次“+”运算符。可以将E写为 E1+E2，其中E1和E2是某些表达式。因为E中正好有 n +1个操作数，而且E1和E2都一定至少含有这些操作数中的一个，这样一来E1和E2中的操作数都不能超过n个。因此，归纳假设适用于E1和E2，只要它们都不止有一个操作数（因为我们开始时将 n =2作为依据）。有4种情况必须考虑：a是在E1中还是在E2中，以及a是否为E1或E2中唯一的操作数。
(a) E1就是a本身。当E为a+(b+c)时，就是这种情况。这里E1就是a，而E2就是b+c 。在这种情况下，E2就是F，也就是说，E本身就已经是 a+F的形式。
(b)E1含有多个操作数，a是其中一个。比如E=(c+(d+a))+(b+e)
其中E1=c+(d+a),E2=b+e。这里，因为E1的操作数不超过n个，但至少达到了两个，所以可以应用归纳假设，使用交换律和结合律，将E1变成a+E3。因此，E可以变形成（a+E3）。因此，E可以变形为（a+E3）+E2。对该式应用结合律，就能将E进一步变形为a+（E3+E2）。这样，我们就可以选择F为E3+E2，这就证明了这种情况下的归纳步骤。对本例中的E，也可以假设将E1=c+（d+a）变形为a+(c+d)。那么E就可以重新分组为a+（（c+d）+（b+e））。
还有两种情况是E2就是a以及E2含有包括a在内的多个操作数，解决方法和a、b一样。在这四种情况中，都是将E变形为所需的形式。因此，归纳步骤得到了证明，可以得出S（n）对所有n≥2都为真的结论。
所有归纳推理的模板
以下形式的归纳证明，涵盖了具有多个依据情况的完全归纳。它还将弱归纳作为一种特例包含其中，并包含了只有一个依据情况的一般情况。
（1）指定要证明的命题S（n）。声明要通过对n 的归纳，证明S（n）对n≥i0为真。指定i0的值，通常是0或1，但也可以是其他整数。直观地解释n表示什么。
（2）陈述依据情况（一个或多个）。这些将是从i0起到某个整数j0的所有整数。通常j0=i0，不过j0也可以是其他整数。
（3）证明各个依据情况S（i0）,S（i0+1）,…,S（j0）。
（4）声明假设S（i0）,S（i0+1），…，S（n）为真（就是“归纳假设”），并要证明S（n+1）,以此来建立归纳步骤。声明自己在假设n≥j0，也就是n至少要跟最大的依据情况一样大。通过用n+1替换S（n）中的n来表示S（n+1）。
（5）在（4）中提到的假设下证明S（n+1）。如果归纳为弱归纳而不是完全归纳，那么证明中只需要用到S（n），不过用归纳假设中的任一或全部命题都是可以的。
（6）得出S（n）对所有n≥i0（但不一定对更小的n）都为真。
证明程序的属性
我们将深入到这样一个领域：证明程序能完成它声称能做的工作。在这个领域中，归纳证明起着举足轻重的作用。我们将看到一项技术，它可以解释迭代程序在进行循环的过程中在做些什么。如果理解循环在做什么，基本上就能明白需要对迭代程序有哪些了解。
要证明程序中循环的属性，关键是要选择循环不变式（或称归纳断言），也就是每次进入循环中某个特定点时都为真的命题S。然后通过对以某种方式衡量循环次数的参数进行归纳，证明该命题S。例如，该参数可以是我们到达某while循环测试的次数，也可以是for循环中循环下标的值，还可以是某个涉及每次循环时都递增1的程序变量的表达式。
（后面不再往下举例证明了，未来涉及证明的内容一律跳过）
在讲到形如
while (<condition>)
<body>
的while循环时，通常都可以为循环条件测试前的那一点找出合适的循环不变式。一般来说，我们会试着通过对循环次数的归纳来证明循环不变式成立。然后，当条件为假时，可以利用循环不变式以及条件为假的事实，得出一些关于while循环终止后什么为真的有用信息。
不过，与for循环不同的是，可能不存在为while循环计数的变量。更糟的是，尽管for循环可以保证最多只会迭代到循环的限制，我们却没理由相信while循环的条件可能会变为假。因此，证明while循环正确性的部分工作就是要证明while循环最终会终止。一般要通过涉及程序中变量的某个表达式E，按照如下方式一起来证明循环的终止。
(1) 每进行一次循环，E的值至少会减少1。
(2) 如果E的值小到某个指定的常数（比如0），循环条件就为假。
//计算n! int n; cin >> n; int i = 2; int fact = 1; while (i <= n) { fact = i * fact; i++; } cout << fact << endl;
递归定义
在递归定义（或归纳定义）中，我们用一类或多类紧密相关的对象或事实本身来对它们进行定义。这种定义一定不能是无意义的，比如“某个部件是某个有某种颜色的部件”，也不能是似是而非的，比如“当且仅当某事物不是glotz时它才是glotz”。归纳定义涉及：
(1) 一条或多条依据规则，在这些规则中，要定义一些简单的对象；
(2) 一条或多条归纳规则，利用这些规则，通过集合中较小的对象来定义较大的对象。
例如，我们可以通过迭代算法定义了阶乘函数：将1X2X…Xn相乘得到n!。其实，还可以按照以下方式递归地定义n!的值。
严格地讲，应该证明，n!的递归定义可以得出与原来的定义相同的结果，这里不进行证明
各种算术表达式是递归定义的，我们为这种定义的依据指定了原子操作数可以是什么。例如，在C语言中，原子操作数既可以是变量，也可以是常量。然后，归纳过程告诉我们可应用哪些运算符，以及每个运算符可以应用到多少个操作数上。
通常将如下的表达式称作“算术表达式”。
依据。以下类型的原子操作数是算术表达式：
(1) 变量；
(2) 整数；
(3) 实数。
归纳。如果E1和E2是算术表达式，那么以下表达式也是算术表达式：
(1) （E1+E2）
(2) （E1-E2）
(3) （E1×E2）
(4) （E1/E2）
运算符+、-、×和/都是二元运算符，因为它们都接受两个参数。它们也叫作中缀（插入）运算符，因为它们出现在两个参数之间。此外，我们允许减号在表示减法之外，还可以表示否定（符号改变）。这种可能性反映在了第5条，也是最后一条递归规则中：
(5) 如果E是算术表达式，那么 ( -E) 也是。
像规则(5)中的-这样只接受一个操作数的运算符，称为一元运算符。它也称为前缀运算符，因为它出现在参数之前。
出现在其参数之后的一元运算符，比如表达式n!中的阶乘运算符!，称为后缀运算符。如果接受多个操作数的运算符重复地出现在其所有参数之前或之后，那么它们也可以是前缀或后缀运算符。在C语言或普通算术中没有这类运算符的例子，不过我们在后面将要讨论一些所有运算符都是前缀或后缀运算符的表示法。接受3个参数的运算符就是三元运算符。举例来说，在C语言中，表示“若c则x，否则y”的表达式c?x:y中，运算符?:就是三元运算符。如果运算符接受k个参数，就称其是k元的。
可以出现在表达式中的圆括号串称为平衡圆括号。例如：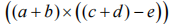
一般来说，判定圆括号串平衡的条件是，每个左圆括号都能与其右侧的某个右圆括号配对。因此，“平衡圆括号串”的一般定义由以下两个规则组成：
(1) 平衡圆括号串中左圆括号和右圆括号的数量相等；
(2) 在沿着括号串从左向右行进的过程中，该串的量变从不为负值，其中量变是对行进过程中已达到左括号数目减去已到达右括号数目的累计值。请注意，统计值必须从0开始，以0结束。例如：
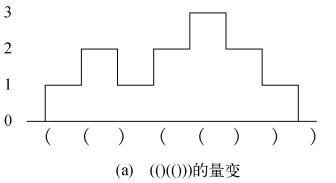
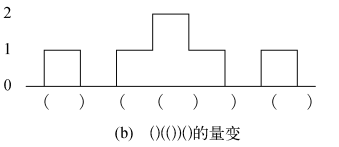
“平衡圆括号”的概念有着多种递归定义。下面的定义比较巧妙，（不进行证明）
依据。空字符串是平衡圆括号串。
归纳。如果x和y是平衡圆括号串，那么（x）y也是平衡圆括号串。
递归函数
递归函数是那些在自己的函数体中被调用的函数。这种调用通常是直接的，例如，函数F在它自己中包含对F的调用。不过，有时候这种调用也会是间接的，比如，某函数F1直接调用函数F2，F2又直接调用F3，等等，直到该调用链中的函数Fk调用F1。
通常可以通过模仿待实现程序的规范中的递归定义，来设计递归算法。实现递归定义的递归函数将含有一个依据部分与一个归案部分。依据部分一般会检查可由定义的依据解决的简单输入（不需要递归调用）。函数的归纳部分则需要一次或多次对其本身进行递归调用，并实现定义的归纳部分。下面的例子应该能说明这几点。
int fact(int n) { if (n <= 1) return 1;//依据 else return n * fact(n - 1);//归纳 }
如果将底层算法表示为如下形式，就可以将图2-2中的SelectionSort函数变成递归函数 recSS。此处假设要排序的数据是在数组A[0..n-1]中。
(1) 从数组A的尾部，也就是从A[i..n-1]中，选出最小的元素。
(2) 将步骤(1)中选出的元素与A[i]互换。
(3) 将剩下的数组A[i+1..n-1]进行排序。
我们可以用递归法表示选择排序
void recSS(int A[], int i, int n) { int j, small, temp; if (i < n - 1) //依据是i=n-1，在这种情况下，该函数会返回而不改变 { //归纳如下 small = i; for (j = i + 1; j < n; j++) { if (A[j] < A[small]) { small = j; } } temp = A[small]; A[small] = A[i]; A[i] = temp; recSS(A, i + 1, n); } }
浙公网安备 33010602011771号