方格稿纸题解

0-序言

本题主要考察的是二维差分以及二维前缀和的知识，已经熟练掌握的大佬可以直接康代码了。。。

1.1 一维

此类问题可表述为给定一个长度为 \(n\) 的序列 \(a\)，多次求长度为 \(k\) 的区间 \(a_i\) 至 \(a_j\) 之和(不包括 \(a_i\) )。
例题

1.1.1 一维前缀和

我们可以定义为 \(s_i=s_{i-1}+a_i\).
表示 \(s_i\) 的前缀和就是 \(s_i\) 加上 \(s_{i-1}\) 的前缀和.

1.1.2 一维差分

定义为 \(b_i=s_i-s_{i-k}\)

1.2 二维

理解一维后，我们再来看二维，二维只是上升了一个维度，在一维的基础上变通一下就可以了
可以理解为：
1.加上/减去沾边的
2.减去/加上重复加/减的，3.最后加上自己/无。

1.2.1 二维前缀和

\(s_{i,j}=s_{{i-1,}j}+s_{i,{j-1}}-s_{i-1,j-1}+a_{i,j}\)
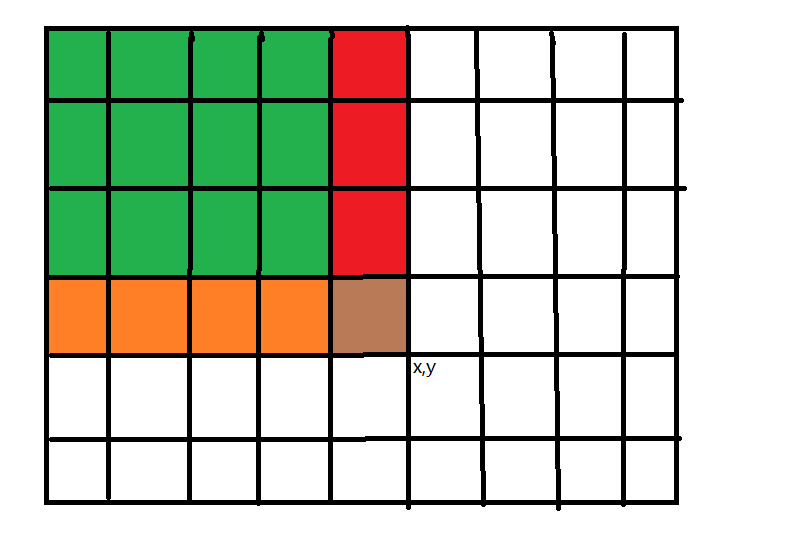
下图为例，要求所有有颜色区域的总和（\(s_{i,j}\)）
绿色和橙色部分是 \(s_{i,j-1}\)，绿色和红色是 \(s_{{i-1,}j}\)。
绿色部分多加了一次，所以要减掉，最后加上 \(a_{i,j}\)

1.2.2 二维差分

以下图为例，要求红色区域总和（\(b_{i,j},k\)）
\(b_{i,j}=s_{i,j}-s_{i-k,j}-s_{i,j-k}+s_{i-k,j-k}\)

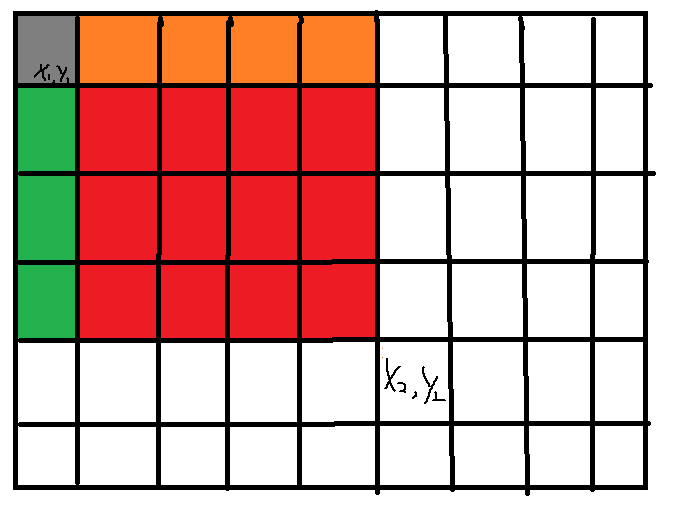
用 \(s_{i,j}\) (所有有颜色区域）减去 \(s_{i-k,j}\)（绿色和灰色部分）再减去
\(s_{i,j-k}\)（橙色和灰色部分），可以发现灰色部分被减了两次，再加回 \(s_{i-k,j-k}\) .

2 复杂度分析

很简单，模拟方块长度是一层，寻找i、j需要两层，总共就是\(\theta(nm·min(n,m))\)

3 代码

#include<iostream>
#include<cmath>
using namespace std;
struct qq
{
    int black=0,white=0;
};
int cnt;
qq a[305][305];
int main()
{
    int n,m,i,j,park;
    cin>>n>>m;
    if(n<2||m<2)
    {
        cout<<0;
        return 0;
    }
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=m;j++)
        {
            cin>>park;
            if(park==1)
            {
                a[i][j].black++;
            }
            else
            {
                a[i][j].white++;
            }
            a[i][j].black+=a[i-1][j].black+a[i][j-1].black-a[i-1][j-1].black;
            a[i][j].white+=a[i-1][j].white+a[i][j-1].white-a[i-1][j-1].white;
        }
    }
    for(int k=2;k<=min(n,m);k++)
    {
        for(i=k;i<=n;i++)
        {
            for(j=k;j<=m;j++)
            {
                int black_cnt=a[i][j].black-a[i-k][j].black-a[i][j-k].black+a[i-k][j-k].black;
                int white_cnt=a[i][j].white-a[i-k][j].white-a[i][j-k].white+a[i-k][j-k].white;
                if(abs(black_cnt-white_cnt)<=1)
                {
                    cnt++;
                }
            }
        }
    }
    cout<<cnt;
    return 0;
}

感谢各位阅读！