[ICCV2023]Inducing Neural Collapse to a Fixed Hierarchy-Aware Frame for Reducing Mistake Severity

这篇文章基于神经坍缩（Neural Collapse）现象，提出将样本的特征诱导到考虑类别层次的Simplex ETF（Equivalent Tight Frame）。首先，通过类别层次距离构建类别间的相似度。基于相似度，通过特征值分解构造固定的分类器权重向量。同时，增加隐藏层鼓励模型特征与对应类别的分类器权重向量对齐。广泛的对比试验和消融实验表明了作者方法的有效性。

背景知识

神经坍缩（Neural Collapse）

神经坍缩最早由 [1] 提出。它指出，在深度神经网络训练过程中，分类器向量倾向于形成简单对称结构，这个结构被称为simplex Equiangular Tight Frame, ETF。在这个结构中，向量两两之间夹角相同。它包括：

NC1：同一类别的不同样本，特征变异性（variability）坍缩到0；它们的特征趋向于类均值。
NC2：类均值坍缩到单纯形等角紧架构（Simplex ETF）， \(\cos(\mathbf{v}_{i}\mathbf{v}_{j})=-\frac{1}{K-1},\ \mathbf{v}_i\in\mathbb{R}^d,\ d\ge K-1\)。其中K是类别数。
NC3：自对偶性（self-duality），分类器向量也呈现ETF，和分类器矩阵和特征矩阵为线性关系：\(\frac{W}{\|W\|_F}=\frac{H}{\|H\|_F}\)。
NC4：对于样本标签预测，简化为选择与特征欧氏距离最近的类别均值。

Prevalence of Neural Collapse During the Terminal Phase of Deep Learning Training. Proceedings of the National Academy of Sciences of the United States of America (PNAS), 117, 09 2020.

不平衡数据集上的神经坍缩

神经坍缩造成的simplex ETF，让所有的类别两两间保持相同的夹角。然而，但训练的数据集是不平衡时，多个少数类可能坍缩到相同的向量。[2] 中发现：随着不平衡率增加，尾部类间的分类器权重向量余弦相似度趋近于1.

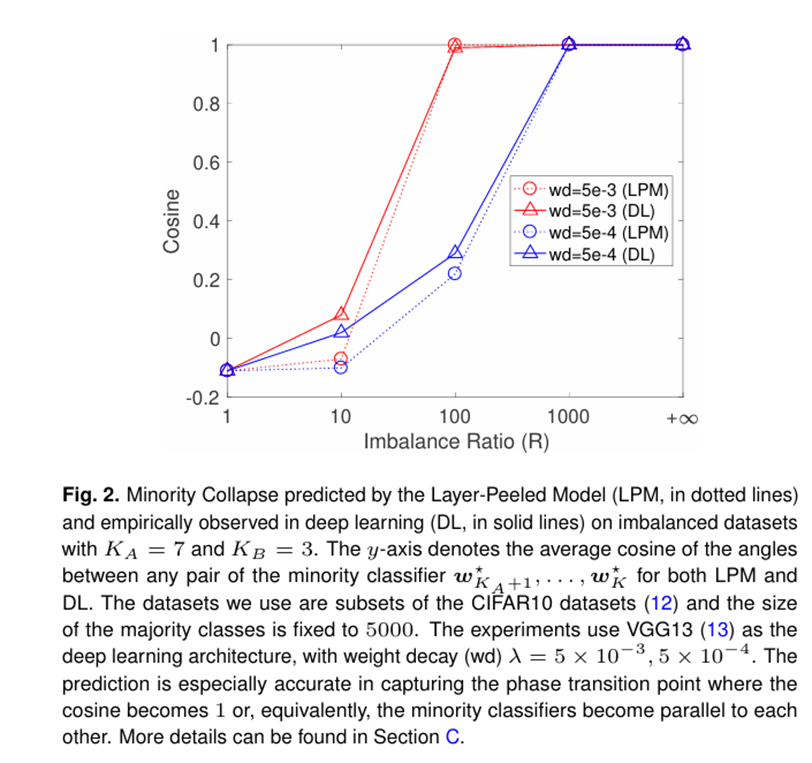
Exploring deep neural networks via layer-peeled model: Minority collapse in imbalanced training. Proceedings of the National Academy of Sciences of the United States of America (PNAS), 2021.

针对不平衡数据集上的神经坍缩，一些工作提出改进：

预先计算构造固定的ETF分类器权重，鼓励特征与固定的ETF对齐。
增加额外的正则项诱导神经坍缩

神经坍缩的局限性

当使用ETF分类错误时，它可能会随机错分到任意一个类。
传统的神经网络使用交叉熵损失和one-hot标签，忽视了潜在的层次关系。

然而在现实中，同样是分类错误，一些分类错误可能更严重，例如：将“狗” -> “狼”，比“狗” -> “猫”更严重。因此有必要在评估时，引入分类错误严重性。

方法

基于ETF，提出考虑包含了层次距离关系的ETF，并将分类器权重固定到层次ETF。图中，以A为例，A与B的夹角更小，A与C和D夹角相同且更大。

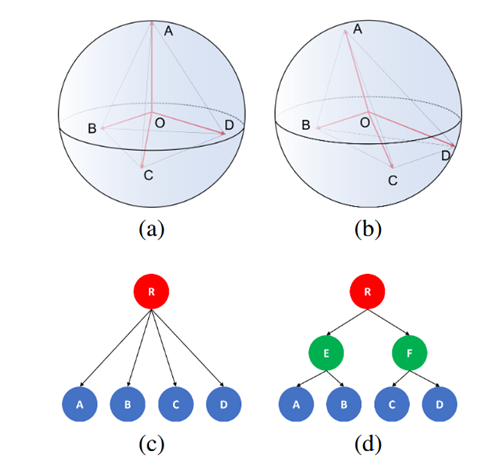
在训练时，通过一个辅助的基于相似度的损失项、和交叉熵损失，让特征诱导、坍缩到预先定义的层次ETF。

相似度的量化

这里相似度不是向量间的相似度，而是离散的类别间的相似度。首先计算两个类的最近公共祖先（Least Common Ancestor，LCA）的高度（叶子节点height=0）：

\[d_{i,j}=\mathrm{height}(\mathrm{LCA}(y_i,y_j)) \]

然后基于距离矩阵计算相似度：

\[S_{ij}=(1-s_\mathrm{min})\cdot e^{-\gamma\cdot\frac{d_{ij}}{d_\mathrm{max}}}+s_\mathrm{min} \]

其中\(s_\mathrm{min}\in(-1,1)\)是超参数，\(\gamma\)是超参数，更大的\(\gamma\)让层次距离对相似度的影响更大。

分类器权重构造

分类器权重矩阵由K个列向量组成，且每个向量2范数为1，我们要求\(\mathbf{S}=\mathbf{W}^T\mathbf{W}\)，其中\(\mathbf{W}=[\mathbf{w}_1,\dots,\mathbf{w}_K],\ \mathbf{w}_i\in\mathbb{R}^K,\ ||\mathbf{w}_i||_2=1\)，希望满足任意两个类别的分类器权重相似度等于它们的类别相似度：

\[cos\angle(\boldsymbol{w}_i,\boldsymbol{w}_j)=\boldsymbol{w}_i^T\boldsymbol{w}_j=S_{ij},\forall1\leq i\leq j\leq K \]

我们可通过特征值分解构造，首先\(\mathbf{S}\)是对称方阵，且对角线元素是行最大值，因此它的 K 个主元大于0（\(\begin{bmatrix} a & 1-a \\ b & 1-b \end{bmatrix}\)->\(\begin{bmatrix} a & 1-a \\ 0 & \frac{a-b}{a} \end{bmatrix}\)），K个特征值大于0（也就是正定矩阵）。

\[\mathbf{S}=\mathbf{Q}\mathbf{D}\mathbf{Q}^{T}=(\mathbf{Q}\mathbf{D}^{1/2}\mathbf{U}^{T})(\mathbf{U}\mathbf{D}^{1/2}\mathbf{Q}^{T})=\mathbf{W}^{T}\mathbf{W} \]

这里\(\mathbf{U}\in \mathbb{R}^{K\times K}\)是正交矩阵，是为了避免直接相乘导致部分向量稀疏，通过对随机初始化矩阵QR分解得到。

额外的转换层

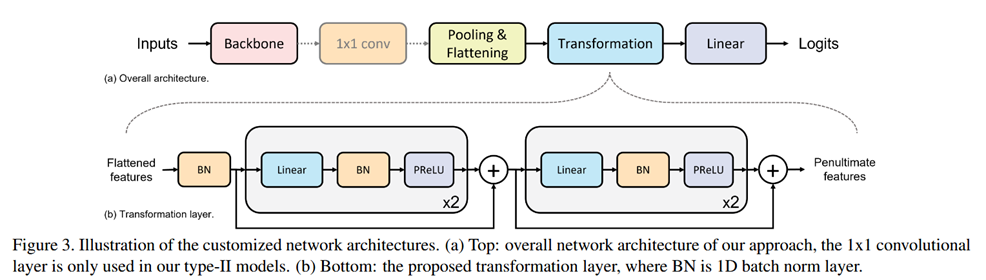
为了更好的让特征坍缩到层次ETF，加入了额外的可学习参数，包括一个 1x1 卷积层，BN层、线性层和激活层。

由于之前的方法都使用ReLU、GELU等激活函数，容易造成非负数的偏置。考虑到层次ETF的分类器权重矩阵含有负数。作者的激活函数选用

\[\mathrm{PReLU}=\begin{cases} x, & \mathrm{if}\ x\ge0 \\ ax, & \mathrm{otherwise} \end{cases} \]

\(a\)是可学习参数，可以学习输入为负数时的斜率。

基于余弦相似度的辅助损失函数

对于标签的预测，取与特征相似度最大的分类器权重向量：

\[\hat{y}=\arg\max_i\boldsymbol{W}^T\boldsymbol{h}=\arg\max_icos\angle(\boldsymbol{w}_i,\boldsymbol{h}) \]

为了使特征更好地坍缩到相应的分类器权重，引入了相似度辅助损失：

\[\mathcal{L}_{COS}=\sum_{i=1}^K(cos\angle(\boldsymbol{w}_i,\boldsymbol{h})-cos\angle(\boldsymbol{w}_i,\boldsymbol{w}_y))^2 \]

当\(\boldsymbol{h}\)与\(\boldsymbol{w}_y\)的对齐时，损失为0.

最终的损失为

\[\mathcal{L}=(1-\alpha)\mathcal{L}_{CE}+\alpha\mathcal{L}_{COS} \]

其中\(\mathcal{L}_{CE}\)是交叉熵损失，\(\alpha\)是超参数。

实验

数据集，模型

数据集涉及了不同层次高度、不同类别数（层次高度是人为预先定义好的）

Dataset	Height	Classes	Train	Val	Test
FGVC-Aircraft	3	100	3,334	3,333	3,333
CIFAR-100	5	100	45,000	5,000	10,000
iNaturalist2019	7	1010	187,385	40,121	40,737
tieredImageNet-H	12	608	425,600	15,200	15,200

由于之前的方法，都是对特征、损失进行操作，并没有直接修改模型架构，因此上面的结构作者称为 Type II。而没有可学习参数引入的，作者称为Type I: (Backbone -> BN -> Linear(in_features, out_features) -> BN -> ELU) 作为Baseline 模型。

评估指标

Top-1 Accuracy
平均错误严重性 (average mistake severity): \(\mathbb{E}_{\mathbb{I}\{y_i!=\hat{y}_i\}}[d_{y_i,\hat{y}_i}]\)。计算所有预测错误的样本，真实标签和预测标签间的层次距离。
前k个平均层次距离 (average hierarchical distance at k): \(\text{HierDist@}K = \mathbb{E}_{i\in N}[\frac{1}{K}\sum_{k=1}^Kd_{y_i,\hat{y}_{i,k}}],\ K=1,5,20\)。计算所有样本中，每个样本前k个置信度最大的预测标签和真实标签的层次距离。

对比实验结果

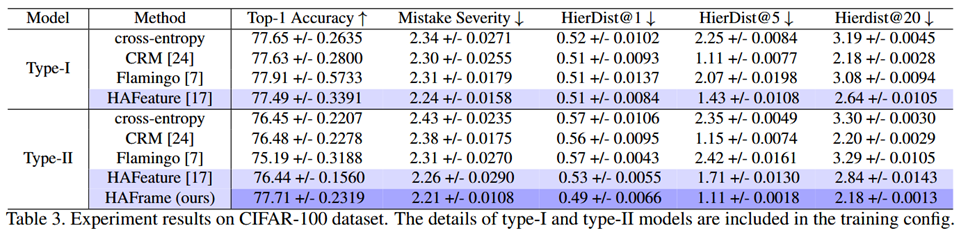
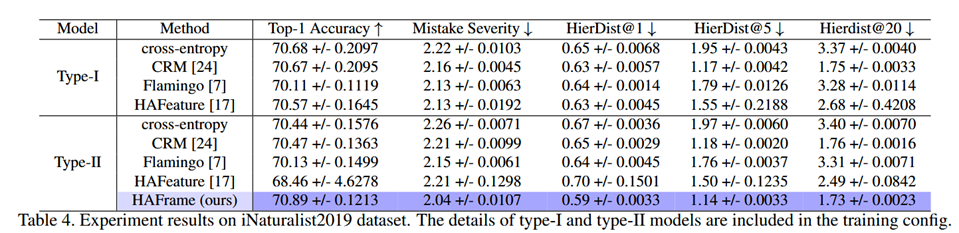
作者的方法在自己改良后的模型架构上取得了较好的结果，这说明，引入额外的参数有助于特征坍缩到层次ETF上。

消融实验

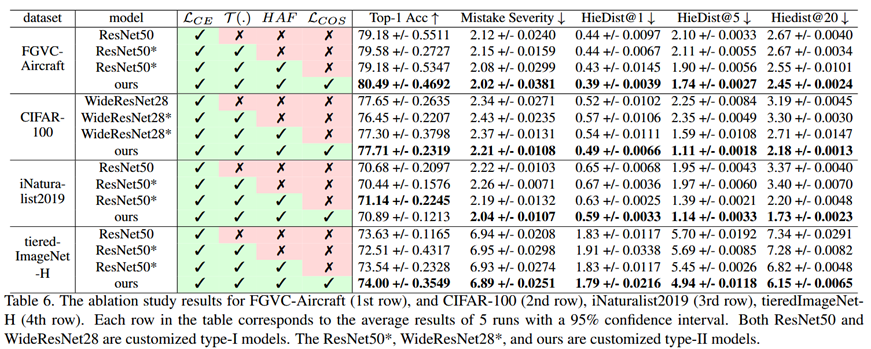
消融实验中，可以看到，单独添加额外的层，并不能提高表现，需要同时搭配层次ETF分类器使用，才能提高结果的表现。

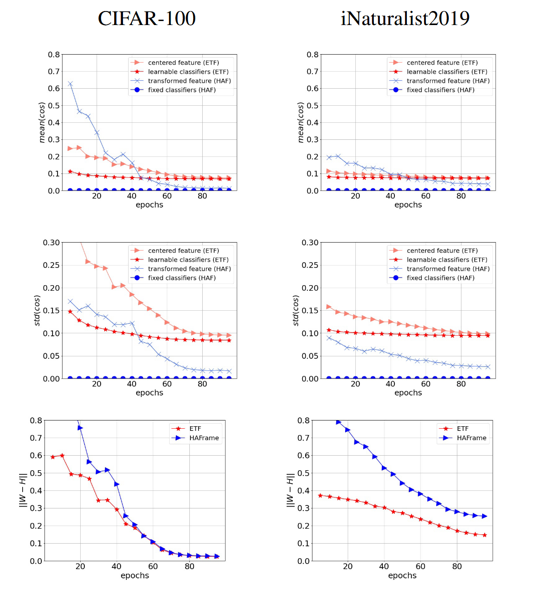
额外的实验：观察训练时的神经坍缩和自对偶

验证是否发生神经坍缩，可观察实际计算的相似度和预定义相似度差的绝对值：

均值：\(Avg_{1\leq i<j\leq K}(|cos\angle(\boldsymbol{x}_i,\boldsymbol{x}_j)-\hat{S}_{ij}|)\)
标准差：\(Std_{1\leq i<j\leq K}(|cos\angle(\boldsymbol{x}_i,\boldsymbol{x}_j)-\hat{S}_{ij}|)\)

特征和分类器权重是否呈自对偶性，可观察它们的F范数差的绝对值：\(\left\|\frac{W}{\|W\|_F}-\frac{H}{\|H\|_F}\right\|_F\)。可以看到，相较于ETF，层次ETF更容易坍缩；但是层次ETF在较大的数据集上较难发生自对偶，需要更多的训练轮次。

参考文献

posted @ 2025-05-25 22:34 片刻的自由阅读(70) 评论(0) 收藏举报

刷新页面返回顶部