算法学习【第八篇】：贪心算法找零问题与分糖果问题

找零问题：假设商店老板需要找零n元钱，钱币的面额有：100元、50元、20元、5元、1元，如何找零使得所需钱币的数量最少？

# greedy algorithm

money = [100,50,20,5,1]

def change_money(x):
    change = [0,0,0,0,0]
    for i,m in enumerate(money):
        change[i] = x // money[i]
        x = x % money[i]   #取余数
    if x > 0:
        print("还剩%s" % x)
    return change

print(change_money(356.2))

分糖果问题

已知有一些孩子和一些糖果，每个孩子都有需求因子g，每个糖果有大小s；如果某个糖果的大小s>=某个孩子的需求因子
时，代表该糖果可以满足该孩子，使用这些糖果，最多可以满足多少孩子？（注意：某个孩子最多只能被一块糖果满足）
1、举个实例
孩子的需求因子为g=[5，10，2，9，15，9]；糖果的大小数组为：s=[6，1，20，3，8]，那么，这种情况下，最多
可以，满足3个孩子。
2、贪心规律
（1）某个糖果不能满足某个孩子，那么，该糖果一定不能满足更大需求因子的孩子。
（2）某个孩子可以用更小的糖果满足，则没必要用更大的糖果，留着更大的糖果去满足需求因子更大的孩子。（贪
心！！）
（3）孩子的需求因子更小则其更容易被满足，故优先从需求因子小的孩子开始，因为用一个糖果满足一个较大需求因子
的孩子或满足较小需求因子的孩子效果一样。（最终总量不变）（贪心！！）
3、算法思路
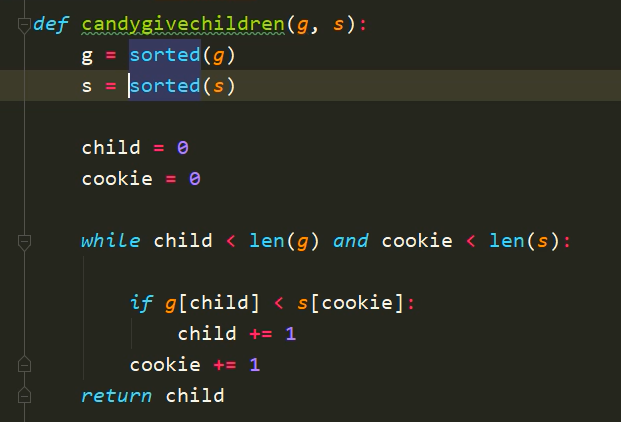
（1）对需求因子数组g和糖果大小数组s进行从小到大排序；

 （2）按照从小到大的顺序使用各糖果，尝试是否可以满足某个孩子，每个糖果只尝试一次，若成功，则换下一个糖果尝试