算法时间复杂度的计算
在我们编程的过程中，可能会遇到这样的情况。（下面只是一个小小的例子，现实中不会这么简单，这里只是取到一个抛砖引玉的作用哈）
计算1-100的和：1+2+3+... ...+100
或者我们直接升级，计算1到n的和：1+2+3+... ...+n
我们不会能那个计算机搁哪儿摁，对不。我们写程序实现之。
那么我们在程序中应该怎样去实现了
有的人可能会这样写：
$a=0;
for ($i=1;$i<=n;$i++){
$a+=$i;
}
echo $a;
这样的写法确实能达到效果，但是当我们的n特别大时，会发生生么样的情况呢？答案是：会发生以下情况（n=100000000000）
计算机没有办法处理这么大的数字。
我们这里就可以引入一个时间复杂度的概念了。
时间复杂度就是
一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。算法的时间复杂度是指执行算法所需要的计算工作量。
我们上面的算法的时间复杂度为T(n) = O(n)
而有的人会这样改写上面的算法
$n = 100000000000;
$a = $n+($n*($n-1)/2);
echo $a;
这样写的结果就是：秒算出来结果
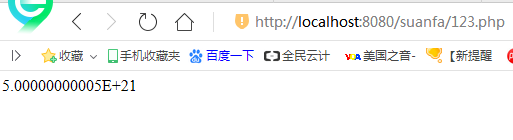
要不要科学计算法可以自己设置的哈。
那为什么下面的这个算法会运行的这么快呢？
因为它只做一次计算，时间复杂度为T(n) = O(1)
通过这个例子，大家应该对时间复杂度有了一个比较入门的印象了。
下面我们来说说具体应该怎样去计算一个算法的时间复杂度。
比如我们有如下算法：
对于顺序执行的语句或者算法，总的时间复杂度等于其中最大的时间复杂度。
void aFunc(int n) {
for (int i = 2; i < n; i++) {
i *= 2;
printf("%i\n", i);
}
}
我们需要计算上述算法的时间复杂度，是不是看的有点懵，放轻松，我们一步步分析。
假设循环次数为 t，则循环条件满足 2^t < n。
可以得出，执行次数t = log(2)(n)，即 T(n) = log(2)(n)，可见时间复杂度为 O(log(2)(n))，即 O(log n)。
再次进阶
long aFunc(int n) {
if (n <= 1) {
return 1;
} else {
return aFunc(n - 1) + aFunc(n - 2);
}
}
是不是更懵了，下面我们来分析：
显然 T(n) = T(n - 1) + T(n - 2) 是一个斐波那契数列，通过归纳证明法可以证明，当 n >= 1 时 T(n) < (5/3)^n，同时当 n > 4 时 T(n) >= (3/2)^n。
所以该方法的时间复杂度可以表示为 O((5/3)^n)，简化后为 O(2^n)。
