python第二章课后习题

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.1.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

import matplotlib.pyplot as plt

def chx(x):
    return (np.exp(x) + np.exp(-x)) / 2

def shx(x):
    return (np.exp(x) - np.exp(-x)) / 2

def half_exp(x):
    return 0.5 * np.exp(x)

x = np.linspace(-5, 5, 1000)  


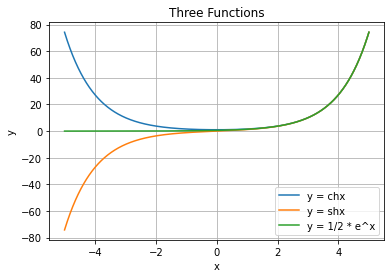
plt.plot(x, chx(x), label='y = chx')


plt.plot(x, shx(x), label='y = shx')


plt.plot(x, half_exp(x), label='y = 1/2 * e^x')

plt.xlabel('x')
plt.ylabel('y')
plt.title('Three Functions')
plt.legend()  
plt.grid(True) 
plt.show()


print("学号：2023310143028")


print("学号：2023310143028")

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.2.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

import matplotlib.pyplot as plt
from scipy.integrate import quad
 
def fun(t, x):
    return np.exp(-t) * (t ** (x - 1))
 
 
x = np.linspace(0, 10, 100)  
y = [quad(fun, 0, np.inf, args=i)[0] for i in x]  
 
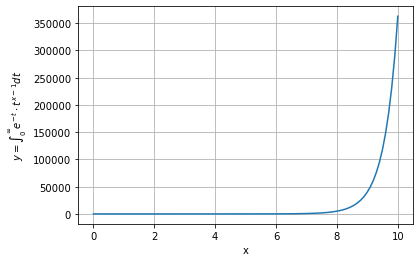
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('$ y = \int_0^{\infty} e^{-t} \cdot t^{x-1} dt $')
plt.grid(True)
plt.show()
 
print("学号：3028")



print("学号：2023310143028")

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.3.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

import numpy as np  
  
 
x = np.linspace(-10, 10, 400) 
  
  
y_values = []  
  
  
for k in range(1, 7):  
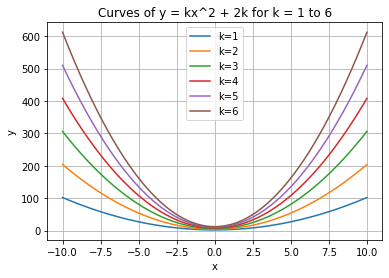
    y = k * x**2 + 2*k  
    plt.plot(x, y, label=f'k={k}')    
    y_values.append(y)    
  
 
plt.legend()  
  
 
plt.title('Curves of y = kx^2 + 2k for k = 1 to 6')  
plt.xlabel('x')  
plt.ylabel('y')  
  
  
plt.grid(True)   
plt.show()


print("学号：2023310143028")

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.4.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

import numpy as np  
  
fig, axs = plt.subplots(2, 3, figsize=(12, 8))  
x = np.linspace(-10, 10, 400)  
  
for k, ax in enumerate(axs.flat, 1):  
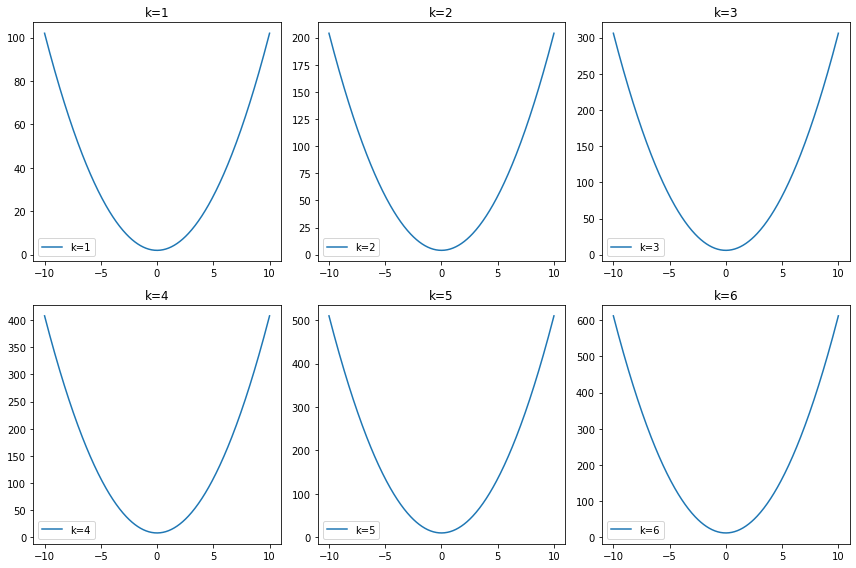
    y = k * x**2 + 2*k  
    ax.plot(x, y, label=f'k={k}')  
    ax.set_title(f'k={k}')  
    ax.legend()  
  
plt.tight_layout()  
plt.show()


print("学号：2023310143028")

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.5.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

import matplotlib.pyplot as plt  
import numpy as np  
  
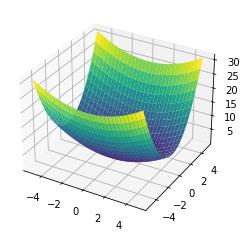
fig = plt.figure()  
ax = fig.add_subplot(111, projection='3d')  
  

a, b = 2, 1  
X = np.outer(np.linspace(-5, 5, 30), np.ones(30))  
Y = X.copy().T  
Z = X**2 / a**2 + Y**2 / b**2  
  
ax.plot_surface(X, Y, Z, cmap='viridis')  
plt.show()


print("学号：2023310143028")

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.6.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

import matplotlib.pyplot as plt  
from mpl_toolkits.mplot3d import Axes3D  
  
 
x = np.linspace(0, 43.65, 40)  
y = np.linspace(0, 58.2, 50)  
X, Y = np.meshgrid(x, y)  
Z = np.sin(np.sqrt(X**2 + Y**2)) * 100  # 使用一个简单的函数来生成高程数据  
  

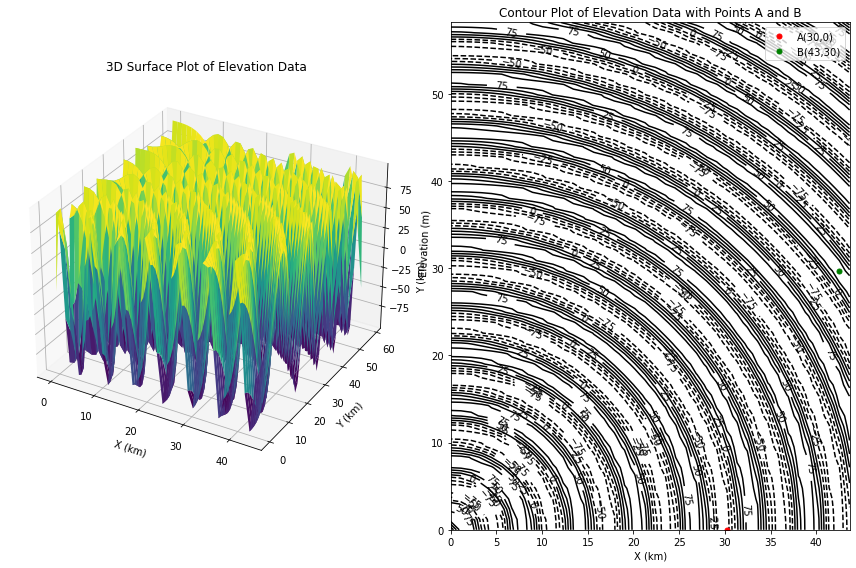
fig = plt.figure(figsize=(12, 8))  
ax = fig.add_subplot(121, projection='3d')  
ax.plot_surface(X, Y, Z, cmap='viridis', edgecolor='none')  
ax.set_xlabel('X (km)')  
ax.set_ylabel('Y (km)')  
ax.set_zlabel('Elevation (m)')  
ax.set_title('3D Surface Plot of Elevation Data')  
  
  
plt.subplot(122)  
CS = plt.contour(X, Y, Z, colors='k')  
plt.clabel(CS, inline=1, fontsize=10)  
  
  
idx_a_x = np.argmin(np.abs(x - 30))  
idx_a_y = np.argmin(np.abs(y - 0))  
idx_b_x = np.argmin(np.abs(x - 43))  
idx_b_y = np.argmin(np.abs(y - 30))  
  
plt.plot(x[idx_a_x], y[idx_a_y], 'ro', markersize=5, label='A(30,0)')  
plt.plot(x[idx_b_x], y[idx_b_y], 'go', markersize=5, label='B(43,30)')  
plt.xlabel('X (km)')  
plt.ylabel('Y (km)')  
plt.title('Contour Plot of Elevation Data with Points A and B')  
plt.legend()  
  
）  
real_area = 43.65 * 58.2  
print(f"Actual Surface Area (ignoring elevation changes): {real_area} km^2")  
  
 
plt.tight_layout()  
plt.show()
 
print("学号：3028")


print("学号：2023310143028")

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.7.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

  
 
A = np.array([[2, 1, -1], [3, -1, 2], [-2, 1, 2]])  
b = np.array([8, -11, -3])  
  
 
if np.linalg.det(A) != 0:  
     
    x = np.linalg.solve(A, b)  
    print("唯一解:", x)  
else:  
    
    x_lsq = np.linalg.lstsq(A, b, rcond=None)[0]  
    print("最小二乘解:", x_lsq)  


print("学号：2023310143028")

唯一解: [ 0.10526316 4.26315789 -3.52631579]

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.8.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

  
 
n = 1000  
A = np.zeros((n, n))  
b = np.arange(1, n+1)  
  
  
for i in range(n):  
    A[i, i] = 4  # 对角线元素为4  
    if i < n-1:  
        A[i, i+1] = 1  # 每一行的下一个元素为1  
    if i > 0:  
        A[i, i-1] = 1  # 每一行的上一个元素为1（除了第一行）  
  

x = np.linalg.solve(A, b)  
  

print("解向量 x:")  
for i in range(n):  
    print(f"x{i+1} = {x[i]:.4f}")
 
print("学号：3028")



print("学号：2023310143028")

x504 = 84.0000
x505 = 84.1667
x506 = 84.3333
x507 = 84.5000
x508 = 84.6667
x509 = 84.8333
x510 = 85.0000
x511 = 85.1667
x512 = 85.3333
x513 = 85.5000
x514 = 85.6667
x515 = 85.8333
x516 = 86.0000
x517 = 86.1667
x518 = 86.3333
x519 = 86.5000
x520 = 86.6667
x521 = 86.8333
x522 = 87.0000
x523 = 87.1667
x524 = 87.3333
x525 = 87.5000
x526 = 87.6667
x527 = 87.8333
x528 = 88.0000
x529 = 88.1667
x530 = 88.3333
x531 = 88.5000
x532 = 88.6667
x533 = 88.8333
x534 = 89.0000
x535 = 89.1667
x536 = 89.3333
x537 = 89.5000
x538 = 89.6667
x539 = 89.8333
x540 = 90.0000
x541 = 90.1667
x542 = 90.3333
x543 = 90.5000
x544 = 90.6667
x545 = 90.8333
x546 = 91.0000
x547 = 91.1667
x548 = 91.3333
x549 = 91.5000
x550 = 91.6667
x551 = 91.8333
x552 = 92.0000
x553 = 92.1667
x554 = 92.3333
x555 = 92.5000
x556 = 92.6667
x557 = 92.8333
x558 = 93.0000
x559 = 93.1667
x560 = 93.3333
x561 = 93.5000
x562 = 93.6667
x563 = 93.8333
x564 = 94.0000
x565 = 94.1667
x566 = 94.3333
x567 = 94.5000
x568 = 94.6667
x569 = 94.8333
x570 = 95.0000
x571 = 95.1667
x572 = 95.3333
x573 = 95.5000
x574 = 95.6667
x575 = 95.8333
x576 = 96.0000
x577 = 96.1667
x578 = 96.3333
x579 = 96.5000
x580 = 96.6667
x581 = 96.8333
x582 = 97.0000
x583 = 97.1667
x584 = 97.3333
x585 = 97.5000
x586 = 97.6667
x587 = 97.8333
x588 = 98.0000
x589 = 98.1667
x590 = 98.3333
x591 = 98.5000
x592 = 98.6667
x593 = 98.8333
x594 = 99.0000
x595 = 99.1667
x596 = 99.3333
x597 = 99.5000
x598 = 99.6667
x599 = 99.8333
x600 = 100.0000
x601 = 100.1667
x602 = 100.3333
x603 = 100.5000
x604 = 100.6667
x605 = 100.8333
x606 = 101.0000
x607 = 101.1667
x608 = 101.3333
x609 = 101.5000
x610 = 101.6667
x611 = 101.8333
x612 = 102.0000
x613 = 102.1667
x614 = 102.3333
x615 = 102.5000
x616 = 102.6667
x617 = 102.8333
x618 = 103.0000
x619 = 103.1667
x620 = 103.3333
x621 = 103.5000
x622 = 103.6667
x623 = 103.8333
x624 = 104.0000
x625 = 104.1667
x626 = 104.3333
x627 = 104.5000
x628 = 104.6667
x629 = 104.8333
x630 = 105.0000
x631 = 105.1667
x632 = 105.3333
x633 = 105.5000
x634 = 105.6667
x635 = 105.8333
x636 = 106.0000
x637 = 106.1667
x638 = 106.3333
x639 = 106.5000
x640 = 106.6667
x641 = 106.8333
x642 = 107.0000
x643 = 107.1667
x644 = 107.3333
x645 = 107.5000
x646 = 107.6667
x647 = 107.8333
x648 = 108.0000
x649 = 108.1667
x650 = 108.3333
x651 = 108.5000
x652 = 108.6667
x653 = 108.8333
x654 = 109.0000
x655 = 109.1667
x656 = 109.3333
x657 = 109.5000
x658 = 109.6667
x659 = 109.8333
x660 = 110.0000
x661 = 110.1667
x662 = 110.3333
x663 = 110.5000
x664 = 110.6667
x665 = 110.8333
x666 = 111.0000
x667 = 111.1667
x668 = 111.3333
x669 = 111.5000
x670 = 111.6667
x671 = 111.8333
x672 = 112.0000
x673 = 112.1667
x674 = 112.3333
x675 = 112.5000
x676 = 112.6667
x677 = 112.8333
x678 = 113.0000
x679 = 113.1667
x680 = 113.3333
x681 = 113.5000
x682 = 113.6667
x683 = 113.8333
x684 = 114.0000
x685 = 114.1667
x686 = 114.3333
x687 = 114.5000
x688 = 114.6667
x689 = 114.8333
x690 = 115.0000
x691 = 115.1667
x692 = 115.3333
x693 = 115.5000
x694 = 115.6667
x695 = 115.8333
x696 = 116.0000
x697 = 116.1667
x698 = 116.3333
x699 = 116.5000
x700 = 116.6667
x701 = 116.8333
x702 = 117.0000
x703 = 117.1667
x704 = 117.3333
x705 = 117.5000
x706 = 117.6667
x707 = 117.8333
x708 = 118.0000
x709 = 118.1667
x710 = 118.3333
x711 = 118.5000
x712 = 118.6667
x713 = 118.8333
x714 = 119.0000
x715 = 119.1667
x716 = 119.3333
x717 = 119.5000
x718 = 119.6667
x719 = 119.8333
x720 = 120.0000
x721 = 120.1667
x722 = 120.3333
x723 = 120.5000
x724 = 120.6667
x725 = 120.8333
x726 = 121.0000
x727 = 121.1667
x728 = 121.3333
x729 = 121.5000
x730 = 121.6667
x731 = 121.8333
x732 = 122.0000
x733 = 122.1667
x734 = 122.3333
x735 = 122.5000
x736 = 122.6667
x737 = 122.8333
x738 = 123.0000
x739 = 123.1667
x740 = 123.3333
x741 = 123.5000
x742 = 123.6667
x743 = 123.8333
x744 = 124.0000
x745 = 124.1667
x746 = 124.3333
x747 = 124.5000
x748 = 124.6667
x749 = 124.8333
x750 = 125.0000
x751 = 125.1667
x752 = 125.3333
x753 = 125.5000
x754 = 125.6667
x755 = 125.8333
x756 = 126.0000
x757 = 126.1667
x758 = 126.3333
x759 = 126.5000
x760 = 126.6667
x761 = 126.8333
x762 = 127.0000
x763 = 127.1667
x764 = 127.3333
x765 = 127.5000
x766 = 127.6667
x767 = 127.8333
x768 = 128.0000
x769 = 128.1667
x770 = 128.3333
x771 = 128.5000
x772 = 128.6667
x773 = 128.8333
x774 = 129.0000
x775 = 129.1667
x776 = 129.3333
x777 = 129.5000
x778 = 129.6667
x779 = 129.8333
x780 = 130.0000
x781 = 130.1667
x782 = 130.3333
x783 = 130.5000
x784 = 130.6667
x785 = 130.8333
x786 = 131.0000
x787 = 131.1667
x788 = 131.3333
x789 = 131.5000
x790 = 131.6667
x791 = 131.8333
x792 = 132.0000
x793 = 132.1667
x794 = 132.3333
x795 = 132.5000
x796 = 132.6667
x797 = 132.8333
x798 = 133.0000
x799 = 133.1667
x800 = 133.3333
x801 = 133.5000
x802 = 133.6667
x803 = 133.8333
x804 = 134.0000
x805 = 134.1667
x806 = 134.3333
x807 = 134.5000
x808 = 134.6667
x809 = 134.8333
x810 = 135.0000
x811 = 135.1667
x812 = 135.3333
x813 = 135.5000
x814 = 135.6667
x815 = 135.8333
x816 = 136.0000
x817 = 136.1667
x818 = 136.3333
x819 = 136.5000
x820 = 136.6667
x821 = 136.8333
x822 = 137.0000
x823 = 137.1667
x824 = 137.3333
x825 = 137.5000
x826 = 137.6667
x827 = 137.8333
x828 = 138.0000
x829 = 138.1667
x830 = 138.3333
x831 = 138.5000
x832 = 138.6667
x833 = 138.8333
x834 = 139.0000
x835 = 139.1667
x836 = 139.3333
x837 = 139.5000
x838 = 139.6667
x839 = 139.8333
x840 = 140.0000
x841 = 140.1667
x842 = 140.3333
x843 = 140.5000
x844 = 140.6667
x845 = 140.8333
x846 = 141.0000
x847 = 141.1667
x848 = 141.3333
x849 = 141.5000
x850 = 141.6667
x851 = 141.8333
x852 = 142.0000
x853 = 142.1667
x854 = 142.3333
x855 = 142.5000
x856 = 142.6667
x857 = 142.8333
x858 = 143.0000
x859 = 143.1667
x860 = 143.3333
x861 = 143.5000
x862 = 143.6667
x863 = 143.8333
x864 = 144.0000
x865 = 144.1667
x866 = 144.3333
x867 = 144.5000
x868 = 144.6667
x869 = 144.8333
x870 = 145.0000
x871 = 145.1667
x872 = 145.3333
x873 = 145.5000
x874 = 145.6667
x875 = 145.8333
x876 = 146.0000
x877 = 146.1667
x878 = 146.3333
x879 = 146.5000
x880 = 146.6667
x881 = 146.8333
x882 = 147.0000
x883 = 147.1667
x884 = 147.3333
x885 = 147.5000
x886 = 147.6667
x887 = 147.8333
x888 = 148.0000
x889 = 148.1667
x890 = 148.3333
x891 = 148.5000
x892 = 148.6667
x893 = 148.8333
x894 = 149.0000
x895 = 149.1667
x896 = 149.3333
x897 = 149.5000
x898 = 149.6667
x899 = 149.8333
x900 = 150.0000
x901 = 150.1667
x902 = 150.3333
x903 = 150.5000
x904 = 150.6667
x905 = 150.8333
x906 = 151.0000
x907 = 151.1667
x908 = 151.3333
x909 = 151.5000
x910 = 151.6667
x911 = 151.8333
x912 = 152.0000
x913 = 152.1667
x914 = 152.3333
x915 = 152.5000
x916 = 152.6667
x917 = 152.8333
x918 = 153.0000
x919 = 153.1667
x920 = 153.3333
x921 = 153.5000
x922 = 153.6667
x923 = 153.8333
x924 = 154.0000
x925 = 154.1667
x926 = 154.3333
x927 = 154.5000
x928 = 154.6667
x929 = 154.8333
x930 = 155.0000
x931 = 155.1667
x932 = 155.3333
x933 = 155.5000
x934 = 155.6667
x935 = 155.8333
x936 = 156.0000
x937 = 156.1667
x938 = 156.3333
x939 = 156.5000
x940 = 156.6667
x941 = 156.8333
x942 = 157.0000
x943 = 157.1667
x944 = 157.3333
x945 = 157.5000
x946 = 157.6667
x947 = 157.8333
x948 = 158.0000
x949 = 158.1667
x950 = 158.3333
x951 = 158.5000
x952 = 158.6667
x953 = 158.8333
x954 = 159.0000
x955 = 159.1667
x956 = 159.3333
x957 = 159.5000
x958 = 159.6667
x959 = 159.8333
x960 = 160.0000
x961 = 160.1667
x962 = 160.3333
x963 = 160.5000
x964 = 160.6667
x965 = 160.8333
x966 = 161.0000
x967 = 161.1667
x968 = 161.3333
x969 = 161.5000
x970 = 161.6667
x971 = 161.8333
x972 = 162.0000
x973 = 162.1667
x974 = 162.3333
x975 = 162.5000
x976 = 162.6667
x977 = 162.8333
x978 = 163.0000
x979 = 163.1667
x980 = 163.3333
x981 = 163.5000
x982 = 163.6667
x983 = 163.8333
x984 = 164.0000
x985 = 164.1667
x986 = 164.3333
x987 = 164.5000
x988 = 164.6667
x989 = 164.8333
x990 = 165.0001
x991 = 165.1663
x992 = 165.3345
x993 = 165.4956
x994 = 165.6832
x995 = 165.7716
x996 = 166.2304
x997 = 165.3067
x998 = 169.5429
x999 = 154.5219
x1000 = 211.3695
学号：3028

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.9.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

  
x, y = sp.symbols('x y')  
  

equation1 = sp.Eq(3*x - 2*y, 23)  
  
 
solutions = sp.solve(equation1, y, dict=True)  
  
print("符号解:", solutions)



print("学号：2023310143028")

符号解: [{y: 3*x/2 - 23/2}]

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.10.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

import numpy as np  
  
  
def V1_quad(y):  
    return np.pi * (4*y - y**2)  
  
V1_corrected, _ = quad(V1_quad, 1, 3)  
  
 
V2 = 0.5 * (4/3) * np.pi * 2**3 - (1/3) * np.pi * 2**2 * 1  
  
 
total_volume_corrected = V1_corrected + V2  
print(total_volume_corrected)
 
import numpy as np  
import math  
  
  
V2 = 4 * math.pi  
y2 = 0.5   
  
  
rho = 1000   
g = 9.81  
  
  
final_y = 10  
delta_E_p = rho * V2 * g * (final_y - y2)  
W = delta_E_p  
  
print(f"圆柱面部分所需功: {W} 焦耳")  
 
 
print("学号：3028")

print("学号：2023310143028")

圆柱面部分所需功: 1171122.909405203 焦耳
学号：3028

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.11.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

  
def f(x):  
    return (abs(x + 1) - abs(x - 1)) / 2 + np.sin(x)  
  
def g(x):  
    return (abs(x + 3) - abs(x - 3)) / 2 + np.cos(x)
 
from scipy.optimize import fsolve  
  
def equation_system(vars):  
    x1, x2, y1, y2 = vars  
    eq1 = 2*x1 - 3*f(y1) - 4*g(y2) + 1  
    eq2 = 3*x2 - 2*f(y1) - 6*g(y2) + 2  
    eq3 = y1 - f(x1) - 3*g(x2) + 3  
    eq4 = 5*y2 - 4*f(x1) - g(x2) + 1  
    return [eq1, eq2, eq3, eq4]  
  
  
initial_guess = [0, 0, 0, 0]  
  
 
solution = fsolve(equation_system, initial_guess)  
  
print("解为：", solution)
 
print("学号：3028")
</details>

解为： [-0.24271363  0.06728599 -0.28798181 -0.37343636]
学号：3028

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.12.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')
<details>
<summary>点击查看代码</summary>

```import numpy as np  
from scipy.linalg import eig  
  
  
A = np.array([[-1, 1, 0],  
              [-4, 3, 0],  
              [1, 0, 2]])  
  
  
eigenvalues, eigenvectors = eig(A)  
  

print("特征值:")  
print(eigenvalues)  
  
 
print("特征向量:")  
for i in range(eigenvectors.shape[1]):  
    print(f"特征值 {eigenvalues[i]:.2f} 对应的特征向量:")  
    print(eigenvectors[:, i].real)  # 取实部，因为有时特征向量会有复数部分，但在这个特定例子中它们是实数
 
print("学号：3028")

print("学号：2023310143028")

特征值:
[2.+0.j 1.+0.j 1.+0.j]
特征向量:
特征值 2.00+0.00j 对应的特征向量:
[0. 0. 1.]
特征值 1.00+0.00j 对应的特征向量:
[ 0.40824829 0.81649658 -0.40824829]
特征值 1.00+0.00j 对应的特征向量:
[ 0.40824829 0.81649658 -0.40824829]
学号：3028

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题2.13.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

  
def f(x):  
    return (abs(x + 1) - abs(x - 1)) / 2 + np.sin(x)  
  
def g(x):  
    return (abs(x + 3) - abs(x - 3)) / 2 + np.cos(x)  
  
  
x1_guess = 0.5  
x2_guess = 1.0  
y1_guess = 0.2  
y2_guess = 0.3  
  
 
def create_system(x1, x2, y1, y2):  
    A = np.array([  
        [0, 0, 3*f(y1), 4*g(y2)],  
        [2, 0, 2*f(y1), 6*g(y2)],  
        [f(x1), 3*g(x2), -1, 0],  
        [4*f(x1), g(x2), 0, -1],  
        [1, -3, 0, -10*f(y1)],  
    ])  
    b = np.array([-1, -2, -3, -1, 2])  
    return A, b  
  
 
A, b = create_system(x1_guess, x2_guess, y1_guess, y2_guess)  
  

sol, residuals, rank, s = np.linalg.lstsq(A, b, rcond=None)  
  
print("最小二乘解：")  
print("x1 =", sol[0])  
print("x2 =", sol[1])  
print("y1 =", sol[2])  
print("y2 =", sol[3])  
print("残差平方和：", residuals[0])
 
print("学号：3028")


print("学号：2023310143028")

最小二乘解：
x1 = -0.17277867902432983
x2 = -0.4694091689677689
y1 = 0.4295234103214414
y2 = -0.26396136331851094
残差平方和： 0.19072492658048873
学号：3028