DS博客作业03--树

0.PTA得分截图

1.本周学习总结

1.1 总结树及串内容

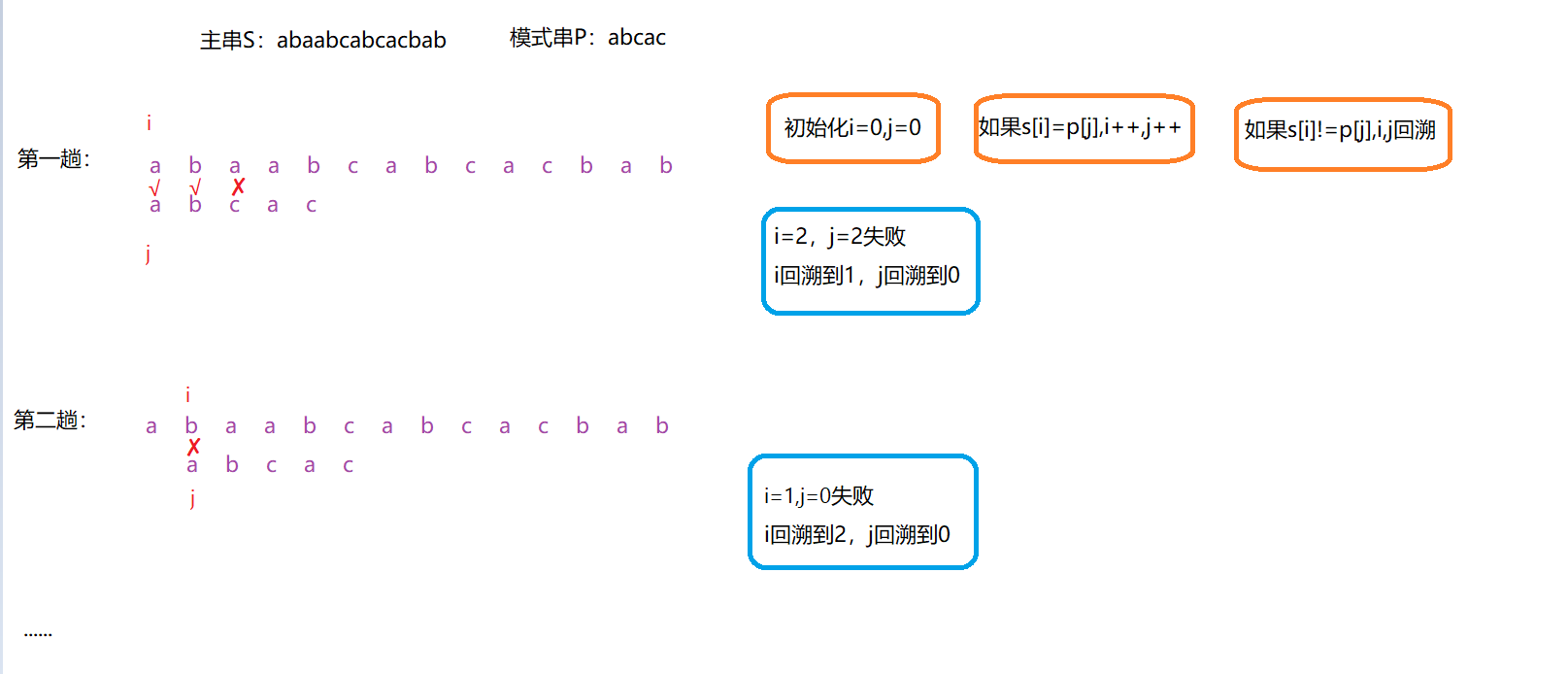
BF算法

实现代码：

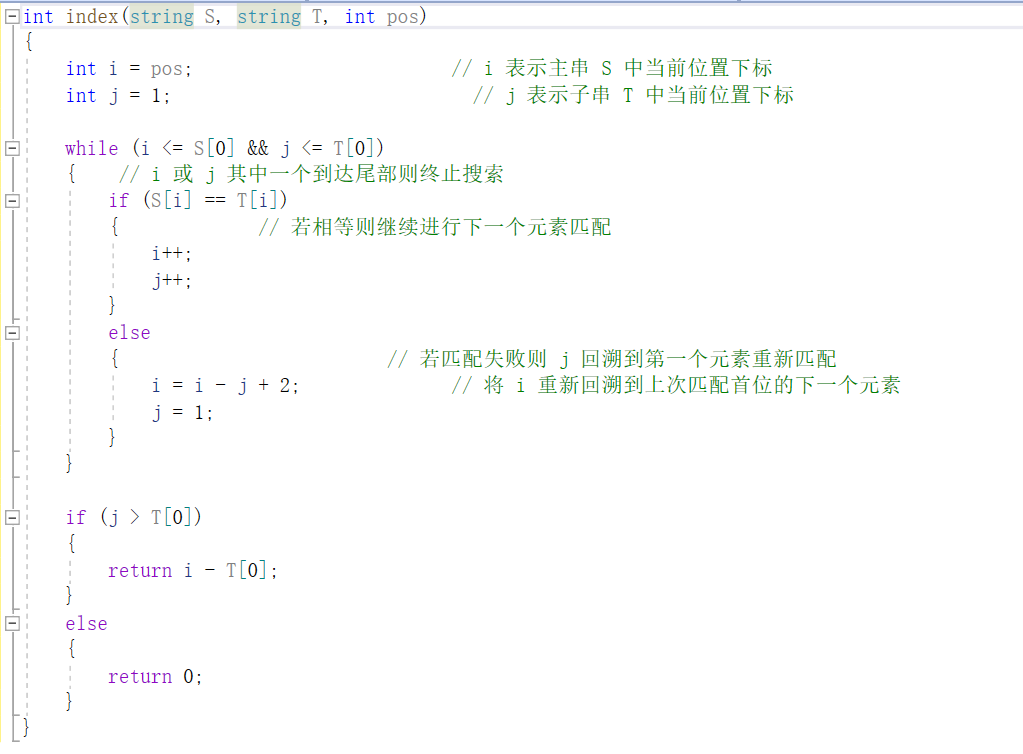
总结：
BF算法在主串和字串匹配失败时，主串进行的回溯操作会影响效率，回溯之后，主串与字串一部分比较是无用的，因此其效率低效。

KMP算法

求next数组算法：

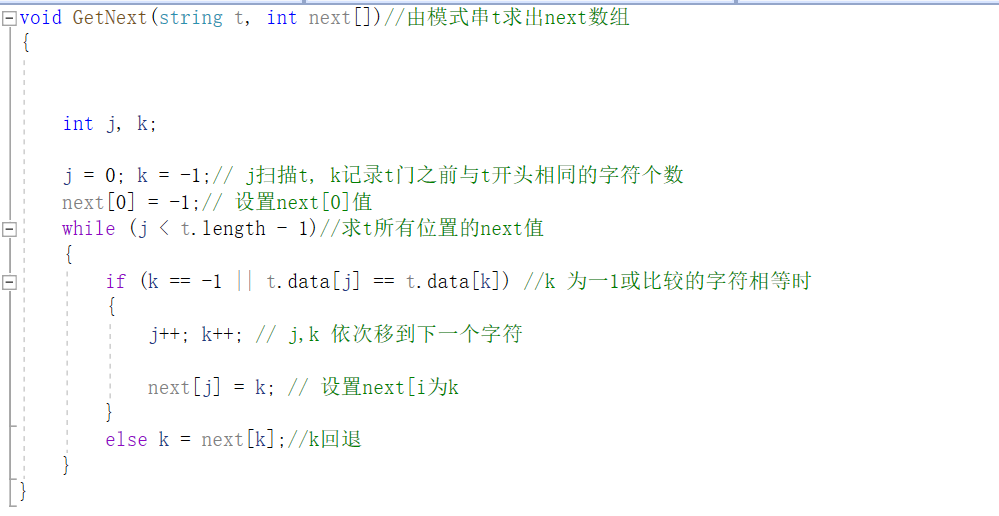
KMP实现代码：

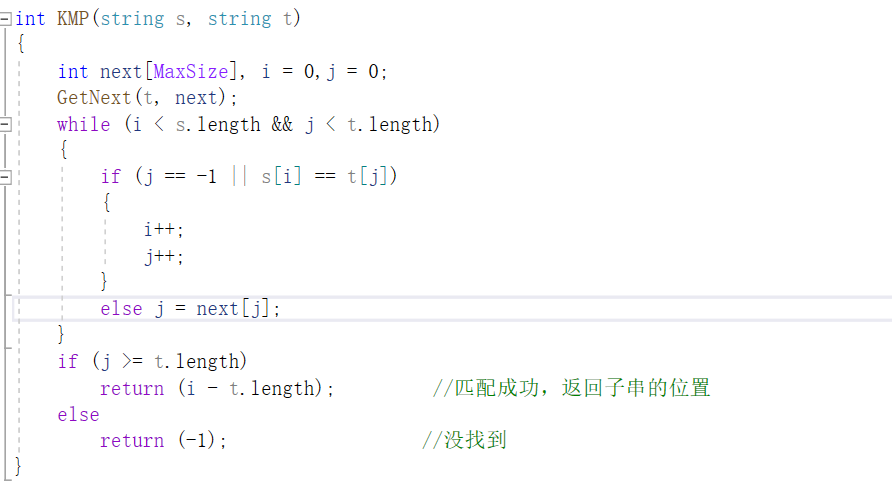
二叉树存储结构

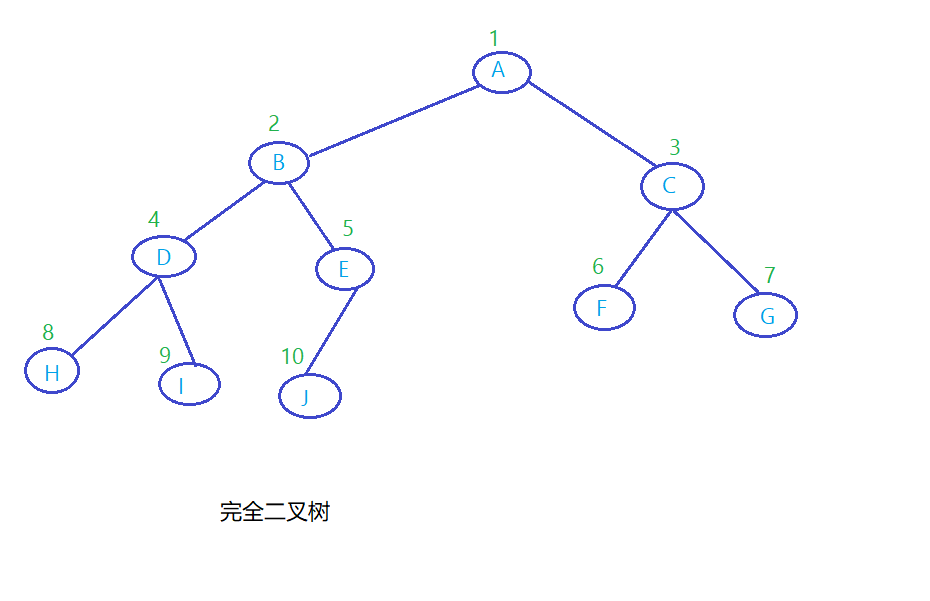
• 顺序存储：
  
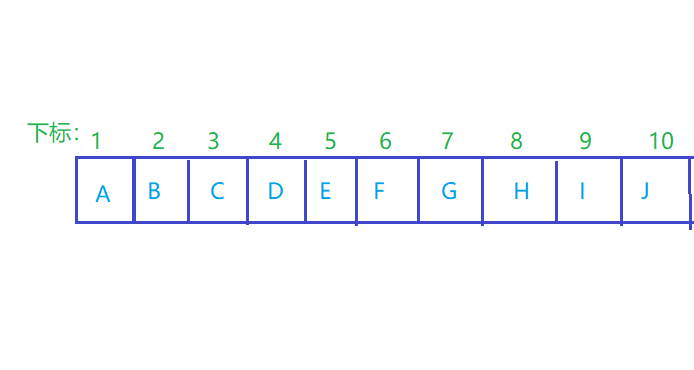
  将这颗二叉树存入到数组中，相应的下表对应其同样的位置，如图：
  
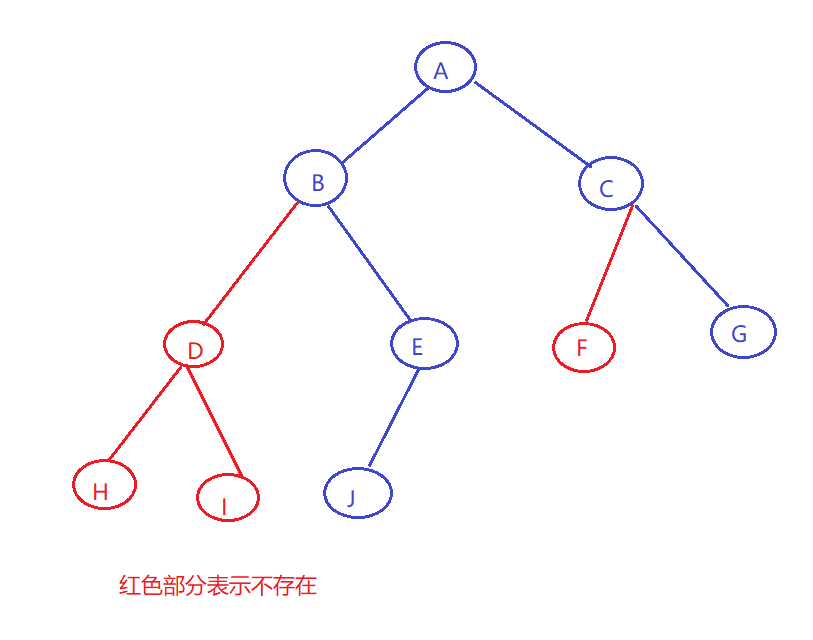
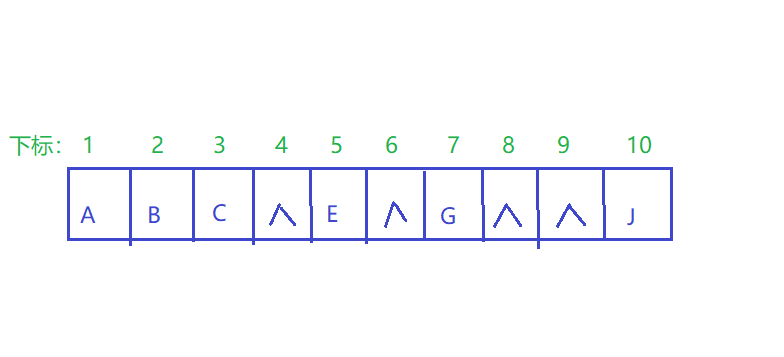
  对于一般的二叉树，尽管层序编号不能反映逻辑关系，但是可以将其按完全二叉树编号，只需把不存在的结点设置为^。
  
  相应的下表对应其同样的位置，如图：
  
• 二叉链表
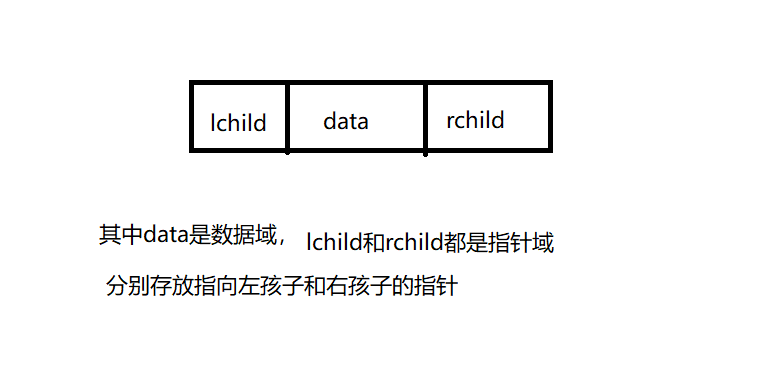
  二叉树最多有两个孩子，所以可以设计一个数据域和两个指针域，这样的链表叫做二叉链表。结构图如下：
  
  二叉链表的结点结构定义代码：

typedef char TElemType;
typedef struct BinaryTreeNode{
    TElemType data;    
    struct BinaryTreeNode *lchild;//lchild指向左结点的指针
    struct BinaryTreeNode *rchild;//rchild指向右结点的指针
}BinaryTreeNode,*BinaryTree;

二叉树的建立及遍历

建二叉树：先输入根，再输入左子树，再输入右子树（左边优先）

void CreatBiTree(BiTree &T)
{
    TElemType ch;
cin >> ch;
if(ch == '#')    //#代表为空
        T = BULL;
else
    {
        T = new BiTNode;    //生成根节点
if(!T)
exit(1);
        CreatBiTree(T->lchild); //构造左子树
        CreatBiTree(T->rchild); //构造右子树
    }
}

遍历二叉树:
二叉树的的遍历主要分为4种：前序遍历，中序遍历，后序遍历，层序遍历
前序遍历：若树为空返回，不为空先访问根节点，再访问左子树，再访问右子树（根左右）
递归法的前序遍历：

void PreOrderTraverse(BiTree T)
{
if(!T)
return ;
else
    {
cout << T->data;
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}

中序遍历：若树为空返回，不为空先访问左子树，再访问根节点，再访问右子树（左根右）
递归法的中序遍历：

void InOrderTraverse(BiTree T)
{
if(!T)
return ;
else
    {
        InOrderTraverse(T->lchild);
cout << T->data;
        InOrderTraverse(T->rchild);
    }
}

后序遍历：若树为空返回，不为空先访问左子树，再访问右子树，再访问根节点（左右根）
递归法的后序遍历：

void PostOrderTraverse(BiTree T)
{
if(!T)
return ;
else
    {
        PostOrderTraverse(T->lchild);
        PostOrderTraverse(T->rchild);
cout << T->data;
    }
}

层次遍历：用一个队列保存被访问的当前节点的左右孩子以实现层序遍历

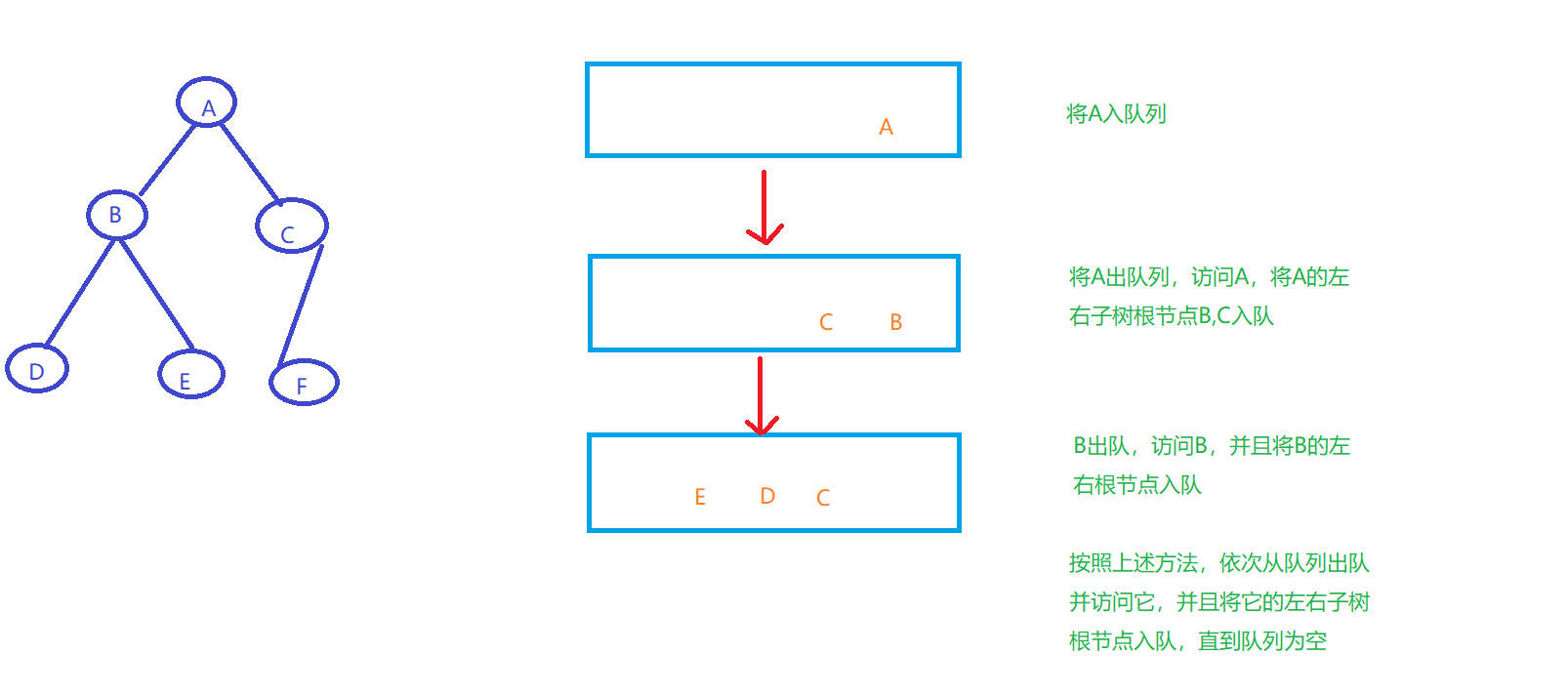
void BinaryTreeLevelOrder(BiNode* root)
 {
    Queue q;
    
    if(root == NULL) //树为空直接返回
   {
        return;
    }
    //初始化队列
    QueneInit(&q);
    //先将根节点入队
    QueuePush(&q, root);
    while (!QueueEmpty(&q))
    {
        //出队保存队头并访问
        BiNode *p= QueuePop(&q);
        visit(p->data);
        if(p->lchild)
        {
            QueuePush(&q, p->lchild);
        }
        if(p->rchild)
        {
            QueuePush(&q, p->rchild);
        }
    }
    DestroyQueue(q);  // 释放队列空间
    return;
}

二叉树的应用：

1.输出二叉树中的叶子结点，利用先序遍历

void PreOrderTraversal ( BinTree BT )
{
if ( BT )
{
if( !BT -> Left && !BT -> Right )
printf ( “%d”, BT -> Data );
PreOrderTraversal ( BT -> Left );
PreOrderTraversal ( BT -> Right );
}
}

2.求二叉树的高度

void PostOrderGetHeight ( BinTree BT )
{     int HL, HR, MaxH ;
if ( BT )
{
HL = PostOrderGetHeight ( BT -> Left ); // 求左子树的深度
HR = PostOrderGetHeight ( BT -> Right ); //求右子树的深度
MaxH = ( HL > HR ) ? HL : HR ; //取左右子树较大的深度
return ( MaxH + 1 ); //返回树的深度
}
else return 0; // 空树深度为0
}

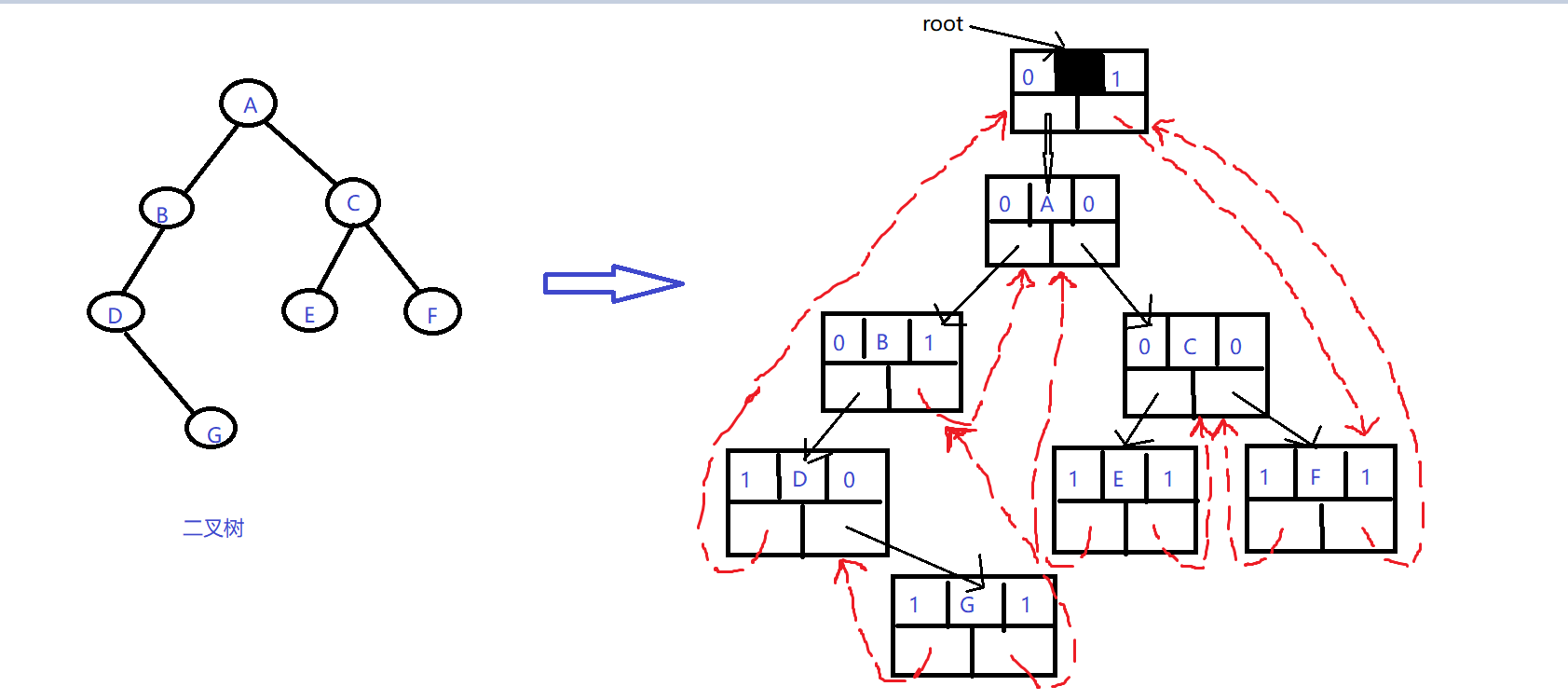
线索二叉树

• 当某结点的左指针为空时,令该指针指向这个线性序列中该结点的前驱结点;当某结点的右指针为空时，令该指针指向这个线性序列中该结点的后继结点,这样的指向该线性序列中的“前驱结点”和“后继结点”的指针称为线索。
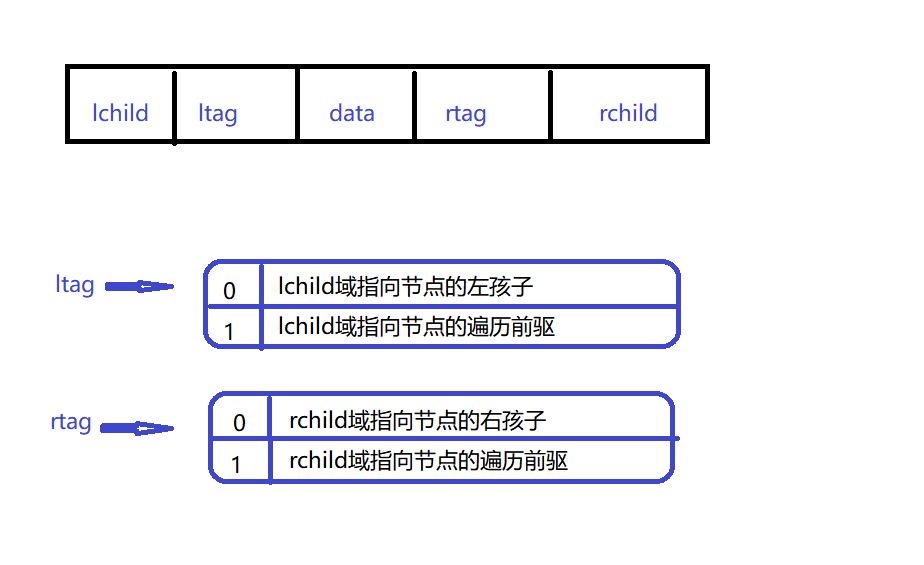
  其节点存储结构：
  

二叉树的二叉链表结点结构定义:

typedef char DataType;
typedef struct Node
{
    DataType data;//结点数据
    struct Node * LChild;//左孩子指针
    struct Node * RChild;//右孩子指针
    int Ltag;//左标记位
    int Rtag;//右标记位
}BiTNode, * BiTree;

二叉树的线索化

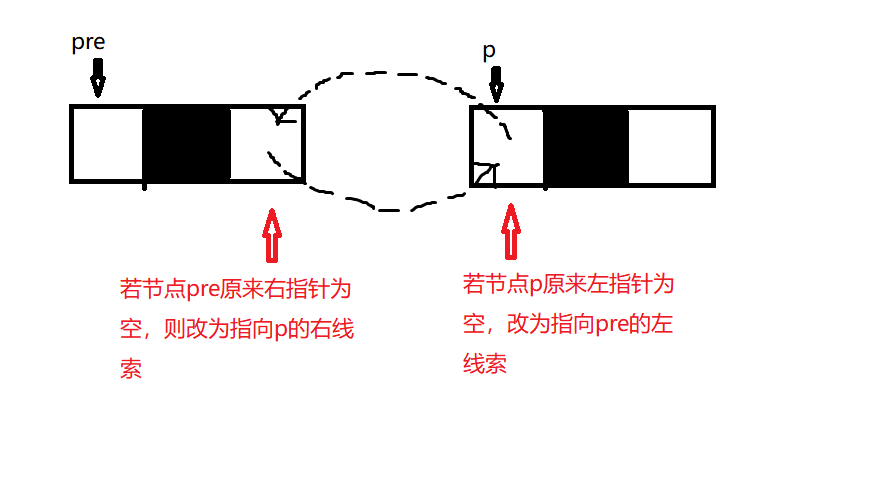
• 空节点的线索化：
  

中序线索二叉树算法：

TBTNode * pre;

void Thread(TBTNode* &p)
{
 if (p!= NULL)
   {
    Thread(o-> lchild)//左子树线索化
    if (p-> lchild= = NULL)//左孩子不存在.进行前驱结点线索化
       {
        p-> lehild= pre;//建立当前结点的前驱结点线索
        p->ltag=1;
       }
    else
        p->lag=0;//p结点的左子树已线索化
    if (pre -> rchild== NULL)//对pre的后继结点线索化
      {
       pre -> rchild= p;//建立前驱结点的后继结点线索
       pre->rtag=1:
      }
    else
        pre->rtag=0 ;
    pre=p;
    Thread(p -> rchild) ;//右子树线索化
    }
}
TBTNode * CreateThread(TBTNode *b)//中序线索化二叉树
{
   TBTNode * root;
   root= (TBTNode * malloec( sizcof(TBTNode)); //创建头结点
   root-> ltag=0;root-> rtag=1;
   root -> rchild= b
   if (b== NULL)//空二叉树
       root > lchild= root;
   else
   {
       root -> lchild= b;
    pre= root;//pre是结点p的前驱结点，供加线索用
    Thread(b);//中序遍历线索化二叉树
    pre -> rchild= root;//最后处理，加入指向头结点的线索
    pre-> rtag=1;
    root -> rchild= pre;//头结点右线索化
   }
    return root;
}

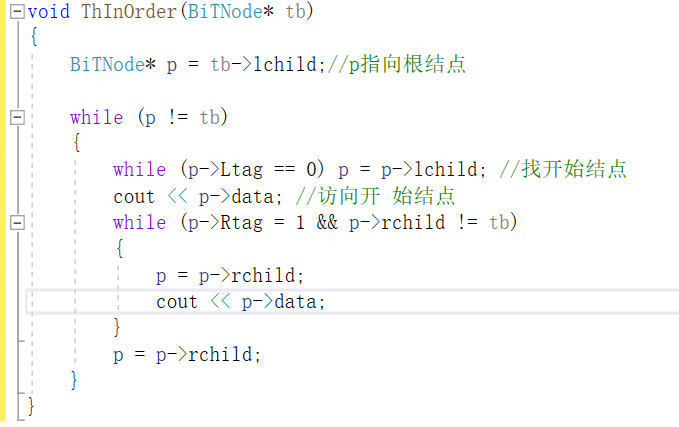
遍历线索化二叉树

伪代码：

p指向根结点;
while(p!=root)
{
 找开始结点p;
 访问p结点;
 while(p结点有右线索)
      一直访问下去;
 P转向右孩子结点:
}

其对应算法：

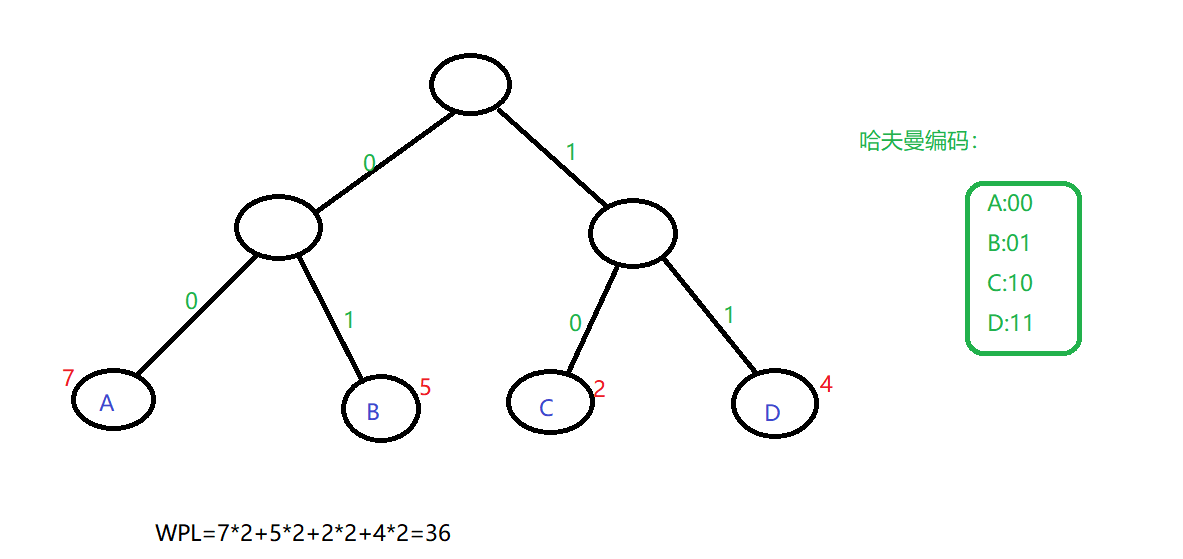
哈夫曼树与并查集

• 基本概念：
  路径:从一个结点到另一个结点之间的分支序列。
  路径长度:从一个结点到另一个结点所经过的分支数目。
  结点的权:树中每个结点所赋子的具有某种实际意义的实数。结带权路径长度:从树根到某一结点的路径长度与该结点的权的乘积。
  内树的带权路径长度:树中从根到所有叶子结点的各个带权路径长度之和。
  

哈夫曼树构建过程：

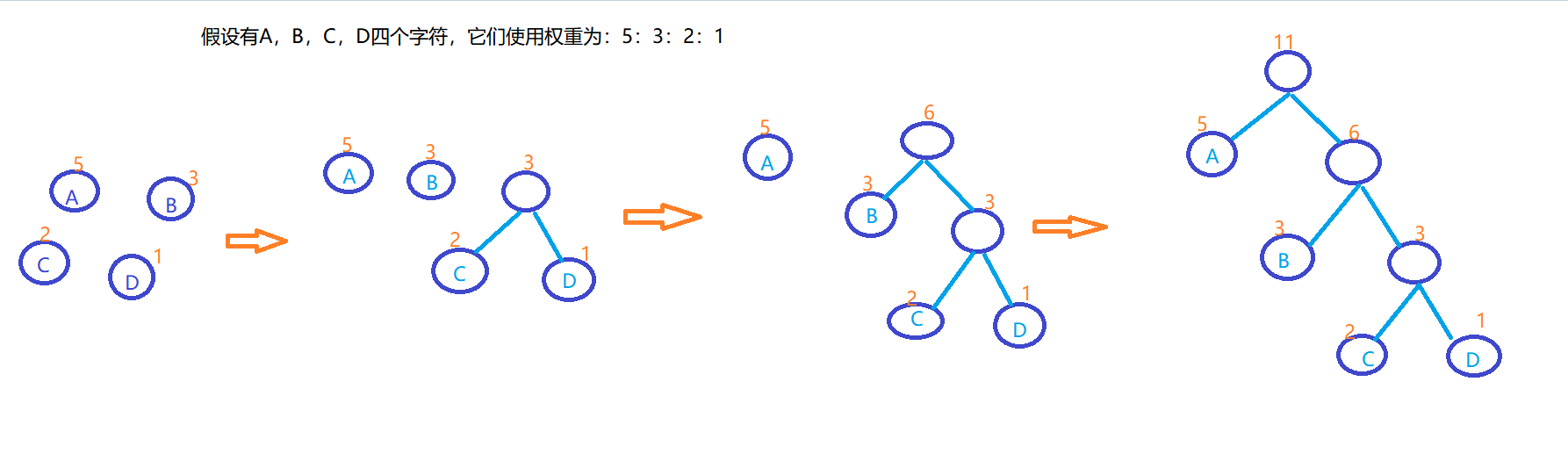
并查集树的结点类型：

始化并查集树：

查找一个元素所属集合：

两个元素各自所属集合的合并：

1.2.谈谈你对树的认识及学习体会。

• 本章主要学习树与二叉树的内容，感觉内容多又复杂，不花很多时间是不会消化得完的，树就分为很多种，若满二叉树，完全二叉树等等，它们的构建就有很多种方法，还有先序，中序，后序等遍历方法，其中又分为递归和非递归的方式，总之构建起来不会像线性表那样方便，因为有的构建方式需要借助栈和队列来来构建，应用的时候要用到很多知识点，所以经常会思绪混乱，无从下手。

2.阅读代码

2.1 题目及解题代码

题目：二叉树最大宽度

解题代码：

2.1.1 该题的设计思路

• 本题使用层序搜索，我们要记录每一层中最左边结点的位置，如果根结点是深度1，那么每一层的结点数就是 2n-1，那么每个结点的位置就是 [1, 2n-1] 中的一个，假设某个结点的位置是i，则其左右子结点的位置分别为 2i 和 2i+1。所以，每一层的宽度为为当前层的 最右边的节点编号减去最左边的编号。

2.1.2 该题的伪代码

int widthOfBinaryTree(TreeNode* root)
{
 if(根节点为空)返回0
 初始化队列
 将根节点入队
 while(队列不空)
 {
  重置编号并将左边编号等于右边编号
     while(队列长度不为0）
     { 
      取队头元素
      右边编号等于第二个元素
      出队
      if(左孩子不空)将左孩子的编号入队
      if(右孩子不空)将右孩子的编号入队
     }
     当前层的宽度=最右边的节点编号减去最左边的编号
 }
}

2.1.3 运行结果

2.1.4分析该题目解题优势及难点

• BFS层序搜索是本题最优解法，可以防止爆int。难点是我们要理解题目所说的最大宽度不是满树的时候的最大宽度，若是满树的最大宽度，则是最后一层的结点数最多。本题的最大宽度应该是两个存在的结点中间可容纳的总的结点个数，中间的结点可以为空。所以我们要求每一层中最左边和最右边的结点的位置，才能算出每一层的宽度，从而求出最大宽度。

2.2 题目及解题代码

题目：根据二叉树创建字符串

解题代码：

2.2.1 该题的设计思路

• 采用前序遍历的方式，省略不必要的括号，将一个二叉树转换成由括号和整数的字符串。当左右子树都为空时， 省略所有括号;当右子树为空，左子树不为空,省略右子树括号；当左子树为空，右子树不为空,左子树括号保留。

2.2.2 该题的伪代码

首先返回空字符串
if(根节点为空)返回0
if(左子树或右子树不为空)给左子树打上括号并递归构造左子树
if(右子树不为空)给右子树打上括号并递归构造右子树

2.2.4分析该题目解题优势及难点

• 本题解题代码比较精简，效率高了许多。难点是左子树和右子树打上括号的条件判断。

2.3 题目及解题代码

题目：搜索树判断

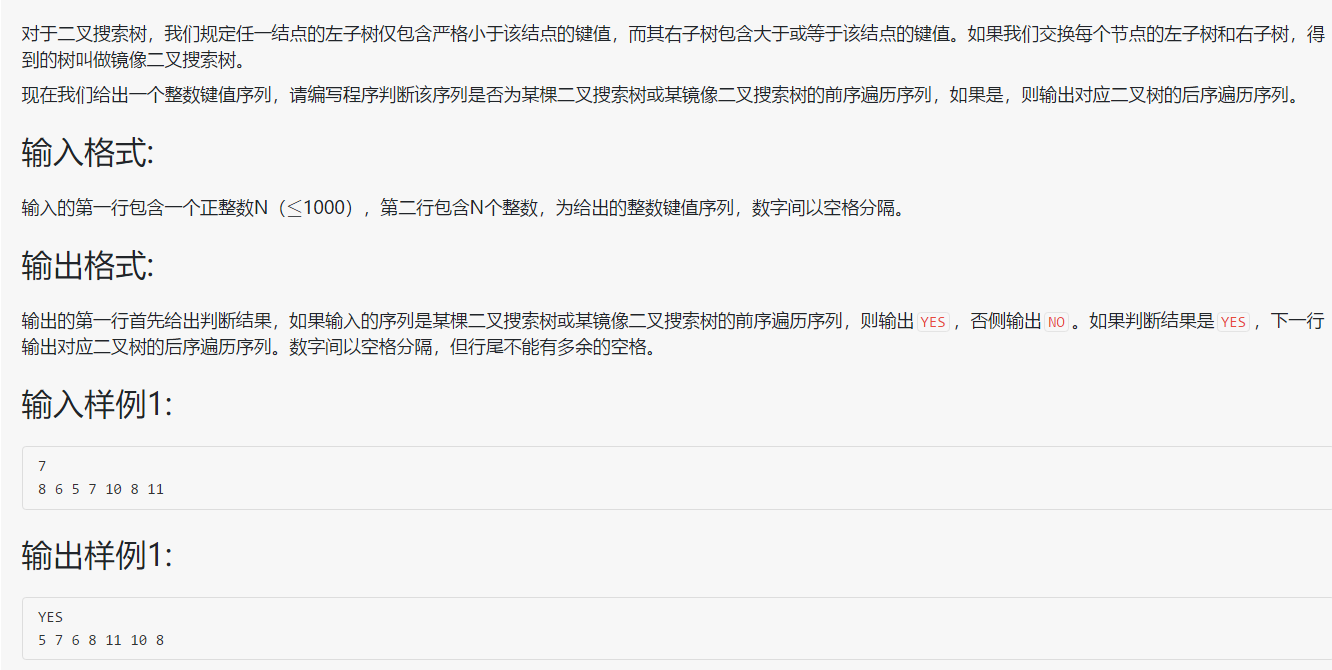
解题代码：

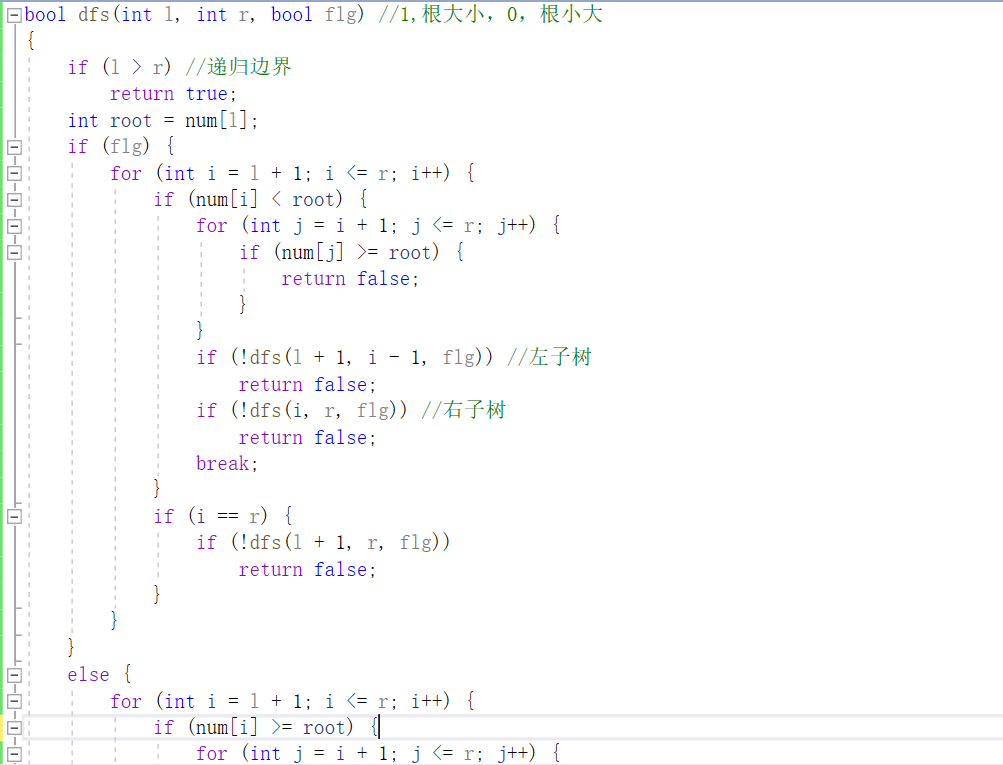
2.3.1 该题的设计思路

• 首先判断序列是否为二叉搜索树，通过先序找大于等于数组第一个数的下标，如果在此数之后的数全都大于等于数组第一个数则是二叉搜索树；判断为二叉搜索树后则通过递归构造树。

2.3.3 运行结果

2.3.4分析该题目解题优势及难点

• 本题运用数组辅助判断是否是二叉搜索树，比较好清晰易懂。难点是理解是二叉搜索树的条件，在大于等于数组第一个数的数后面的数都大于数组第一个数则是二叉搜索树。

2.4 题目及解题代码

题目：堆 笛卡尔树

解题代码：

#include<iostream>
using namespace std;
#define null -1 //表示空
typedef struct BiNode {
    int k1, k2, lchild, rchild;
}BiNode;
BiNode T[1001];
int chick[1001];
int createTree(int n)
{
    for (int i = 0; i < n; i++)
        chick[i] = 0;
    for (int i = 0; i < n; i++)
    {
        cin >> T[i].k1 >> T[i].k2 >> T[i].lchild >> T[i].rchild;
        if (T[i].lchild != -1)
            chick[T[i].lchild] = 1;
        if (T[i].rchild != -1)
            chick[T[i].rchild] = 1;
    }
    for (int i = 0; i < n; i++)
    {
        if (chick[i] == 0)
            return i;
    }
    return null;
}

bool isBST(int r)
{
    int p;
    if (r == null)
        return true;
    if (T[r].lchild == null && T[r].rchild == null)
        return true;
    p = T[r].lchild;
    if (p != null)
    {
        while (T[p].rchild != null)
            p = T[p].rchild;
        if (T[r].k1 < T[p].k1)
            return false;
    }

    p = T[r].rchild;
    if (p != null)
    {
        while (T[p].lchild != null)
            p = T[p].lchild;
        if (T[r].k1 > T[p].k1)
        return false;
    }
    return isBST(T[r].lchild) && isBST(T[r].rchild);
}

bool isHeap(int n)
{
    for (int i = n; i >= 0; i--)
    {
        if (T[i].lchild != null)
        {
            if (T[i].k2 > T[T[i].lchild].k2)
                return false;
        }
        if (T[i].rchild != null)
        {
            if (T[i].k2 > T[T[i].rchild].k2)
                return false;
        }
    }
    return true;
}
int main()
{
    int n, root;
    cin >> n;
    root = createTree(n);
    if (isBST(root) && isHeap(n))
        cout << "YES" << endl;
    else
        cout << "NO" << endl;
    return 0;
}

2.4.1 该题的设计思路

• 笛卡尔树的判定：中序遍历可得到原序列，任意树结点的左子树结点所对应的数列元素下标比该结点所对应元素的下标小，右子树结点所对应数列元素下标比该结点所对应元素下标大。
• 最小堆的判定：采用递归的方式，任意树结点所对应数值大(或小)于其左、右子树内任意结点对应数值。

2.4.2 该题的伪代码

bool isBST(int r)
{
 if(根节点为空)返回true
 if(根节点的左子树和右子树都空)返回true
 if(左子树不空)
  {  
    if(结点左子树的所有K1值都比该结点的K1值大)返回false
  }
  
 if(左子树不空)
  {  
    if(结点右子树的所有K1值都比该结点的K1值大)返回false
  }
}
bool isHeap(int n)
{
 for(i=n to o)
 {
  if(左子树不空)
    {
     if(该结点的K2值比其子树中所有结点的K2值大)返回false
    }
  if(右子树不空)
    {
     if(该结点的K2值比其子树中所有结点的K2值大)返回false
    }
 }
 end for
}

2.4.3 运行结果

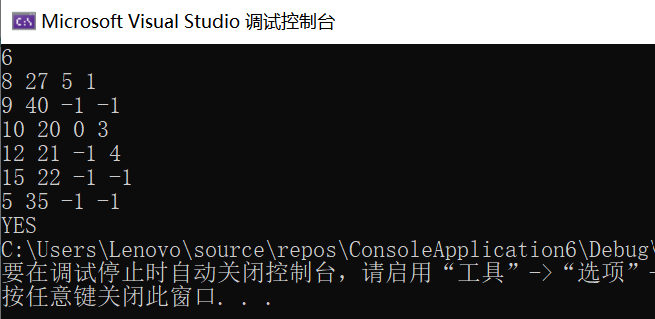
2.4.4分析该题目解题优势及难点

• 本题采用静态树保存树的信息，并记录树的根节点信息，更加方便，简化。难点是理解笛卡尔树的慨念及其判定，还要理解树的堆序性质：笛卡尔树根结点为序列的最大/小值，左、右子树则对应于左右两个子序列，其结点同样为两个子序列的最大/小值。