数据结构与算法

复杂度通常包括时间复杂度和空间复杂度，其中时间复杂度与代码的结构设计高度相关；空间复杂度与代码中数据结构的选择高度相关。

　　1、它与具体的常系数无关，O(n) 和 O(2n) 表示的是同样的复杂度。

　　2、复杂度相加的时候，选择高者作为结果，也就是说 O(n²)+O(n) 和 O(n²) 表示的是同样的复杂度。

　　3、O(1) 也是表示一个特殊复杂度，即任务与算例个数 n 无关。

经验性结论：

　　1、一个顺序结构的代码，时间复杂度是 O(1)。

　　2、二分查找，或者更通用地说是采用分而治之的二分策略，时间复杂度都是 O(logn)。这个我们会在后续课程讲到。

　　3、一个简单的 for 循环，时间复杂度是 O(n)。

　　4、两个顺序执行的 for 循环，时间复杂度是 O(n)+O(n)=O(2n)，其实也是 O(n)。

　　5、两个嵌套的 for 循环，时间复杂度是 O(n²)。

将“昂贵”的时间复杂度转换成“廉价”的空间复杂度

　　降低时间复杂度的方法有递归、二分法、排序算法、动态规划等

　　降低空间复杂度的核心思路就是，能用低复杂度的数据结构能解决问题，就千万不要用高复杂度的数据结构

程序优化的方法：

　　第一步，暴力解法。在没有任何时间、空间约束下，完成代码任务的开发。

　　第二步，无效操作处理。将代码中的无效计算、无效存储剔除，降低时间或空间复杂度。

　　第三步，时空转换。设计合理数据结构，完成时间复杂度向空间复杂度的转移。

 

线性表是 n 个数据元素的有限序列，最常用的是链式表达，通常也叫作线性链表或者链表。在链表中存储的数据元素也叫作结点，一个结点存储的就是一条数据记录。每个结点的结构包括两个部分：

　　第一是具体的数据值；

　　第二是指向下一个结点的指针。

　　单向链表：链表只能通过上一个结点的指针找到下一个结点，反过来则是行不通的。

　　循环链表：最后一个元素的指针指向第一个元素，就得到了循环链表

　　双向链表：有指向下一个结点的指针以外，再增加一个指向上一个结点的指针

　　增：链表在执行数据新增的时候非常容易，只需要把待插入结点的指针指向原指针的目标，把原来的指针指向待插入的结点，就可以了

 

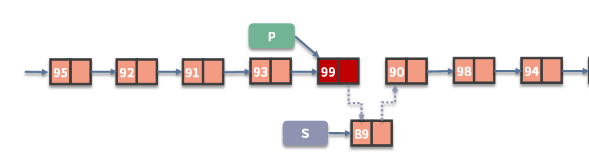
 　　s.next = p.next

　　p.next = s

　　删：待删除的结点为 b，那么只需要把指向 b 的指针 （p.next），指向 b 的指针指向的结点（p.next.next）。

 

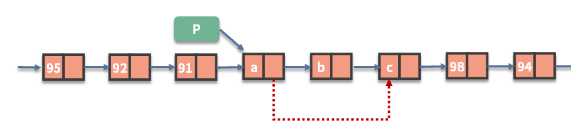
 　　p.next = p.next.next

　　查：费劲

栈：栈是一种特殊的线性表（区别在于增和删）

栈的数据结点必须后进先出。后进的意思是，栈的数据新增操作只能在末端进行，不允许在栈的中间某个结点后新增数据。先出的意思是，栈的数据删除操作也只能在末端进行，不允许在栈的中间某个结点后删除数据。

队列：队列也是一种特殊的线性表，与线性表的不同之处也是体现在对数据的增和删的操作上

队列的特点是先进先出：

先进，表示队列的数据新增操作只能在末端进行，不允许在队列的中间某个结点后新增数据

先出，队列的数据删除操作只能在始端进行，不允许在队列的中间某个结点后删除数据。也就是说队列的增和删的操作只能分别在这个队列的队尾和队头进行

顺序队列，依赖数组来实现，其中的数据在内存中也是顺序存储

链式队列，则依赖链表来实现，其中的数据依赖每个结点的指针互联，在内存中并不是顺序存储。链式队列，实际上就是只能尾进头出的线性表的单链表。

数组增删查的时间复杂度：

　　增加：若插入数据在最后，则时间复杂度为 O(1)；如果中间某处插入数据，则时间复杂度为 O(n)。

　　删除：对应位置的删除，扫描全数组，时间复杂度为 O(n)。

　　查找：如果只需根据索引值进行一次查找，时间复杂度是 O(1)。但是要在数组中查找一个数值满足指定条件的数据，则时间复杂度是 O(n)。

字符串：　　

　　空串，指含有零个字符的串。例如，s = ""，书面中也可以直接用 Ø 表示。

　　空格串，只包含空格的串。它和空串是不一样的，空格串中是有内容的，只不过包含的是空格，且空格串中可以包含多个空格。例如，s = "   "，就是包含了 3 个空格的字符串。

　　子串，串中任意连续字符组成的字符串叫作该串的子串。

　　原串通常也称为主串。例如：a = "BEI"，b = "BEIJING"，c = "BJINGEI" 。

对于字符串 a 和 b 来说，由于 b 中含有字符串 a ，所以可以称 a 是 b 的子串，b 是 a 的主串；

而对于 c 和 a 而言，虽然 c 中也含有 a 的全部字符，但不是连续的 "BEI" ，所以串 c 和 a 没有任何关系。

字符串的存储结构与线性表相同，也有顺序存储和链式存储两种

　　字符串的顺序存储结构，是用一组地址连续的存储单元来存储串中的字符序列，一般是用定长数组来实现。有些语言会在串值后面加一个不计入串长度的结束标记符，比如 \0 来表示串值的终结。

　　字符串的链式存储结构，与线性表是相似的，但由于串结构的特殊性（结构中的每个元素数据都是一个字符），如果也简单地将每个链结点存储为一个字符，就会造成很大的空间浪费。因此，一个结点可以考虑存放多个字符，如果最后一个结点未被占满时，可以使用 "#" 或其他非串值字符补全

分治方法：

　　难度在降低，即原问题的解决难度，随着数据的规模的缩小而降低。这个特征绝大多数问题都是满足的。

　　问题可分，原问题可以分解为若干个规模较小的同类型问题。这是应用分治法的前提。

　　解可合并，利用所有子问题的解，可合并出原问题的解。这个特征很关键，能否利用分治法完全取决于这个特征。

　　相互独立，各个子问题之间相互独立，某个子问题的求解不会影响到另一个子问题。如果子问题之间不独立，则分治法需要重复地解决公共的子问题，造成效率低下的结果。

分治法试用条件：

　　问题的解决难度与数据规模有关；

　　原问题可被分解；

　　子问题的解可以合并为原问题的解；

　　所有的子问题相互独立。

经验之谈：

　　二分查找的时间复杂度是 O(logn)，这也是分治法普遍具备的特性。当你面对某个代码题，而且约束了时间复杂度是 O(logn) 或者是 O(nlogn) 时，可以想一下分治法是否可行。

　　二分查找的循环次数并不确定。一般是达到某个条件就跳出循环。因此，编码的时候，多数会采用 while 循环加 break 跳出的代码结构。

　　二分查找处理的原问题必须是有序的。因此，当你在一个有序数据环境中处理问题时，可以考虑分治法。相反，如果原问题中的数据并不是有序的，则使用分治法的可能性就会很低了。

 

排序：冒泡排序、插入排序、归并排序以及快速排序   排序，就是让一组无序数据变成有序的过程

分析：

　　1．时间复杂度，具体包括，最好时间复杂度、最坏时间复杂度以及平均时间复杂度。

　　2．空间复杂度，如果空间复杂度为 1，也叫作原地排序。

　　3．稳定性，排序的稳定性是指相等的数据对象，在排序之后，顺序是否能保证不变

 

冒泡排序

　　原理：从第一个数据开始，依次比较相邻元素的大小。如果前者大于后者，则进行交换操作，把大的元素往后交换。通过多轮迭代，直到没有交换操作为止。 冒泡排序就像是在一个水池中处理数据一样，每次会把最大的那个数据传递到最后。

　　性能：冒泡排序最好时间复杂度是 O(n)，也就是当输入数组刚好是顺序的时候，只需要挨个比较一遍就行了，不需要做交换操作，所以时间复杂度为 O(n)。　　

　　冒泡排序最坏时间复杂度会比较惨，是 O(n*n)。也就是说当数组刚好是完全逆序的时候，每轮排序都需要挨个比较 n 次，并且重复 n 次，所以时间复杂度为 O(n*n)。

　　很显然，当输入数组杂乱无章时，它的平均时间复杂度也是 O(n*n)。

　　冒泡排序不需要额外的空间，所以空间复杂度是 O(1)。冒泡排序过程中，当元素相同时不做交换，所以冒泡排序是稳定的排序算法。

function bubbleSort(arr){
    for(let i = 1;i< arr.length;i++){
        for(let j = 0;j<arr.length - i;j++){
            if(arr[j] > arr[j+1]){
                let temp = arr[j]
                arr[j] = arr[j + 1]
                arr[j + 1] = temp
            }
        }
    }
    return arr
}

 

插入排序

　　原理：选取未排序的元素，插入到已排序区间的合适位置，直到未排序区间为空。插入排序顾名思义，就是从左到右维护一个已经排好序的序列。直到所有的待排数据全都完成插入的动作。

　　性能：

　　插入排序最好时间复杂度是 O(n)，即当数组刚好是完全顺序时，每次只用比较一次就能找到正确的位置。这个过程重复 n 次，就可以清空未排序区间。

　　插入排序最坏时间复杂度则需要 O(n*n)。即当数组刚好是完全逆序时，每次都要比较 n 次才能找到正确位置。这个过程重复 n 次，就可以清空未排序区间，所以最坏时间复杂度为 O(n*n)。

　　插入排序的平均时间复杂度是 O(n*n)。这是因为往数组中插入一个元素的平均时间复杂度为 O(n)，而插入排序可以理解为重复 n 次的数组插入操作，所以平均时间复杂度为 O(n*n)。

　　插入排序不需要开辟额外的空间，所以空间复杂度是 O(1)。

function  insertSort(arr) {
    for (let i = 1;i<arr.length;i++) {
        let temp = arr[i]
        for(var j = i - 1; j >= 0; j--){
            if(arr[j] > temp){
                arr[j+1] = arr[j]
            } else {
                break
            }
        }
        arr[j+1] = temp
    }
    return arr
}

 

插入排序和冒泡排序算法的异同点

相同点

　　插入排序和冒泡排序的平均时间复杂度都是 O(n*n)，且都是稳定的排序算法，都属于原地排序。

差异点

　　冒泡排序每轮的交换操作是动态的，所以需要三个赋值操作才能完成；

　　而插入排序每轮的交换动作会固定待插入的数据，因此只需要一步赋值操作。

 

归并排序：

　　原理：归并排序的原理其实就是我们上一课时讲的分治法。它首先将数组不断地二分，直到最后每个部分只包含 1 个数据。然后再对每个部分分别进行排序，最后将排序好的相邻的两部分合并在一起，这样整个数组就有序了

　　性能：

　　　　对于归并排序，它采用了二分的迭代方式，复杂度是 logn。

　　　　每次的迭代，需要对两个有序数组进行合并，这样的动作在 O(n) 的时间复杂度下就可以完成。因此，**归并排序的复杂度就是二者的乘积 O(nlogn)。**同时，它的执行频次与输入序列无关，因此，归并排序最好、最坏、平均时间复杂度都是 O(nlogn)。

　　　　空间复杂度方面，由于每次合并的操作都需要开辟基于数组的临时内存空间，所以空间复杂度为 O(n)。归并排序合并的时候，相同元素的前后顺序不变，所以归并是稳定的排序算法。

 

function Merger(a, b){
    let n = a && a.length;
    let m = b && b.length;
    let c = [];
    let i = 0, j = 0;

    while (i < n && j < m)
     {
         if (a[i] < b[j])
             c.push(a[i++]);
         else
             c.push(b[j++]); 
     }

    while (i < n)
         c.push(a[i++]);

    while (j < m)
         c.push(b[j++]); 
    console.log('归并排序：'+c);
    return c;
}
//归并排序
function merge_sort(arr){
    if(arr.length == 1)
        return arr

    let mid = Math.floor(arr.length/2)
    let left = arr.slice(0,mid)
    let right = arr.slice(mid)

    return Merger(merge_sort(left),merge_sort(right)); //合并左右部分
}

 

快速排序：

　　原理：快速排序法的原理也是分治法。它的每轮迭代，会选取数组中任意一个数据作为分区点，将小于它的元素放在它的左侧，大于它的放在它的右侧。再利用分治思想，继续分别对左右两侧进行同样的操作，直至每个区间缩小为 1，则完成排序。

　　性能：

　　　　在快排的最好时间的复杂度下，如果每次选取分区点时，都能选中中位数，把数组等分成两个，那么此时的时间复杂度和归并一样，都是 O(n*logn)。

　　　　而在最坏的时间复杂度下，也就是如果每次分区都选中了最小值或最大值，得到不均等的两组。那么就需要 n 次的分区操作，每次分区平均扫描 n / 2 个元素，此时时间复杂度就退化为 O(n*n) 了。

　　　　快速排序法在大部分情况下，统计上是很难选到极端情况的。因此它平均的时间复杂度是 O(n*logn)。

　　　　快速排序法的空间方面，使用了交换法，因此空间复杂度为 O(1)。

　　　　很显然，快速排序的分区过程涉及交换操作，所以快排是不稳定的排序算法

function quickSort(arr,low,high){
    let i,j,temp,t;
    if(low >= high){
        return
    }
    i = low;
    j = high;
    temp = arr[low]
    while(i< j){
        //右边
        while(temp <= arr[j] && i <j){
            j--;
        }
        while(temp >= arr[i] && i < j){
            i++;
        }
        t = arr[i];
        arr[j] = arr[i];
        arr[i] = t;
    }
    arr[low] = arr[i];
    arr[i] = temp;
    //递归左
    quickSort(arr,low, j - 1);
    //递归右
    quickSort(arr, j + 1, high);
}

 动态规划：

动态规划问题之所以难，是因为动态规划的解题方法并没有那么标准化，它需要你因题而异，仔细分析问题并寻找解决方案。虽然动态规划问题没有标准化的解题方法，但它有一些宏观层面通用的方法论：

　　k 表示多轮决策的第 k 轮

　　分阶段，将原问题划分成几个子问题。一个子问题就是多轮决策的一个阶段，它们可以是不满足独立性的。

　　找状态，选择合适的状态变量 Sk。它需要具备描述多轮决策过程的演变，更像是决策可能的结果。

　　做决策，确定决策变量 uk。每一轮的决策就是每一轮可能的决策动作，例如 D2 的可能的决策动作是 D2 -> E2 和 D2 -> E3。

　　状态转移方程。这个步骤是动态规划最重要的核心，即 sk+1= uk(sk) 。

　　定目标。写出代表多轮决策目标的指标函数 Vk,n。

　　寻找终止条件。

 

策略，每轮的动作是决策，多轮决策合在一起常常被称为策略。

策略集合，由于每轮的决策动作都是一个变量，这就导致合在一起的策略也是一个变量。我们通常会称所有可能的策略为策略集合。因此，动态规划的目标，也可以说是从策略集合中，找到最优的那个策略。

一般而言，具有如下几个特征的问题，可以采用动态规划求解：

最优子结构。它的含义是，原问题的最优解所包括的子问题的解也是最优的。例如，某个策略使得 A 到 G 是最优的。假设它途径了 Fi，那么它从 A 到 Fi 也一定是最优的。

无后效性。某阶段的决策，无法影响先前的状态。可以理解为今天的动作改变不了历史。

有重叠子问题。也就是，子问题之间不独立。这个性质是动态规划区别于分治法的条件。如果原问题不满足这个特征，也是可以用动态规划求解的，无非就是杀鸡用了宰牛刀。

 

解决问题步骤：

　　复杂度分析。估算问题中复杂度的上限和下限。

　　定位问题。根据问题类型，确定采用何种算法思维。

　　数据操作分析。根据增、删、查和数据顺序关系去选择合适的数据结构，利用空间换取时间。

　　编码实现。