java--PTA大作业

• 前言

   1.PTA大作业一前言

         本次习题集，共分为九道题，第九道题的难度较大，主要是对于题目各种要求的三角形的判断条件比较多，还有一个浮点数误差问题，是本次习题集较难的一道题目，第一题主要考察一些基本的的语法，较为简单。第二题难度也不大，根据题意列式子就可以解决，注意题目测试点用例为float类型，若使用double类型则不能ac。第三题考察了一下数组的使用，相对简单。第四题难度开始提升，题干相较于前三题更复杂，分支更多，考察了逻辑思维能力，理解透彻题意之后按部就班的实现就可以ac了，只有一种情况需要特判。第五题难度相对第四题又较低，只是一些简单的分支。第六题难度为中等，需要对学号进行识别，考察了对字符串的使用，且需要判断非法输入。第七题难度为中等，考察了浮点型数据的运算及逻辑思维能力，理解题意之后同样一步步去实现就可以。第八题难度中等，需要提取字符串中的01序列，考察了对于字符串的使用，遍历一遍就好。

   2.PTA大作业二前言

   本次习题集，一共分为三道题，第二题的难度较大，条件多，分支复杂，需要多次判断，第一次做对于奇偶校验位概念不清晰，考察了逻辑思维能力与字符串的更深入使用，奇偶校验位是整个字符串再包括这一位数中1的个数是奇数还是偶数，容易错误理解为光靠奇偶校验位来判断，对于不合格数据的判断较为复杂。第一题难度不大，考察了关于ASCII码值与字符之间的运用，。第三题难度不及第二题，但比第一题还是要难一些，同样考察了字符串间的函数及使用，对于非法输入可以使用到正则表达式。

 

   3.PTA大作业三前言

   本次习题集，一共分为三道题，总体三道题都是关于对于点的操作，相比于前两次大作业而言，难度更大，对于点的非法输入判断需要使用到正则表达式并且较为复杂，三道题对于点的操作一题比一题更难更复杂，第三题难度最大，五个功能中三个是对于三个点的操作，一个对于五个点操作，一个对于四个点操作，并且实现起来颇有难度，考察了数学能力以及对于java的类的操作，颇有面对对象的味道。第二道题简单于第三题，但是难度也不小，同样是判断非法输入，功能中考察了数学知识以及编写类的能力。第一题难度最小，只需要判断非法输入和计算两点间距。

 

   三次大作业的难度逐步增加，从普通编程再到面对对象入门，考察的知识面广，还有对于类的设计，使我更加深入的了解到类的使用方法，理解面对对象的含义。

 

   三次大作业的得分情况：

   PTA大作业一: 100分(总分100)

   PTA大作业二: 60分(总分61)

   PTA大作业三:72分(总分100)

 

• 设计与分析

 

  ① PTA大作业二第二题:

    源码如下:

import java.util.Scanner;
public class Main{
    public static void main(String[] args){
        Scanner in= new Scanner (System.in);
        String s = in.nextLine();
        String d[] = new String [100000];
        d[1]=s;
        int n=0;
        int j=1;
        do{
        int i=0; ++n; 
        int flag=0,sum=0;
        int sta = d[j].indexOf('0');
            if(!d[j].contains("0")||d[j].length()<11){
            System.out.println("null data");
            return ;
        }
        System.out.print(n+":");
        
        char a=d[j].charAt(sta+10); char e=d[j].charAt(sta+9);
            for(int o=sta+1;o<=sta+1+8;o++)
            {
                char p=d[j].charAt(o);
                if(p=='1') sum++;
            }
        if(a!='1'){
            System.out.println("validate error");
            flag=1;
        }
        else if(sum%2==0){
            System.out.println("parity check error");
            flag=1;
        }
        for(i=sta+1;i<sta+1+8;i++)
        {
            char c=d[n].charAt(i);
            if(flag==0){
                System.out.print(c);
            }
        }
            if(flag==0) System.out.println();
        d[j+1]=d[j].substring(i+2);
            j++;
        }while((d[j].length())>=11);
    }
}

 

      分析：

  使用indexOf()函数定位到字符串中第一个起始位的下标，从此开始往后八位为有效数据(包括此位)，后两位为奇偶校验位与结束位，然后对这十一位数字进行条件判断，再利用substring()截取从结束位之后一位开始到字符串末尾的字符串，再次对其进行上述步骤，通过Do-while语句进行循环操作，直到不满足条件。

  圈层复杂度:

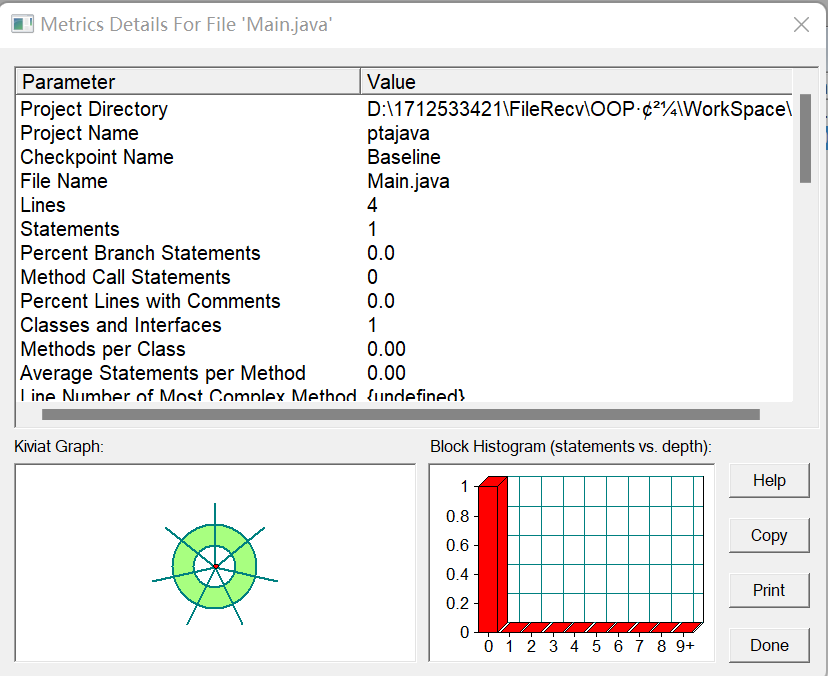
     可见复杂度不高，方法可行。

    

     ② PTA大作业三:

  整个PTA作业三都有一个判断输入合法的问题，而一个一个判断太过于繁琐，由此了解到了正则表达式，

 

        以下是两种做法的对比

 

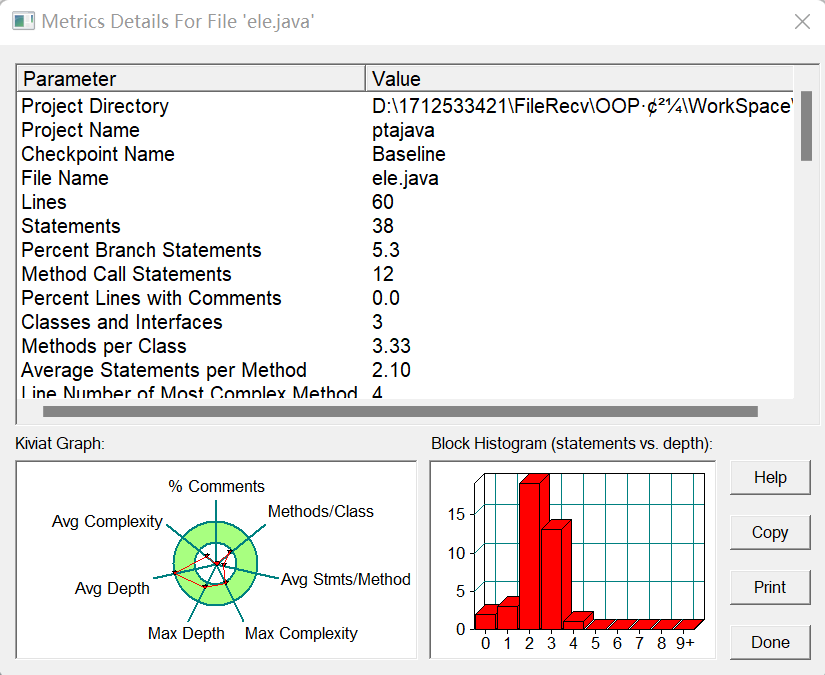
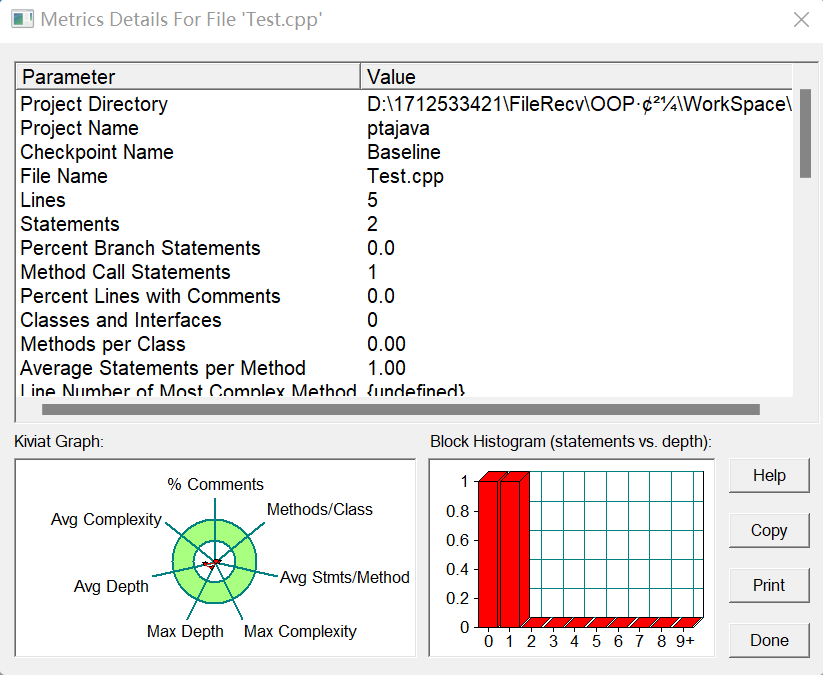
    三道题目都是对于点的格式输入的判断，正则表达式如下:

"^(\\+?|-?)(((0\\.|[1-9]{1}[0-9]*\\.)[0-9]+)|(0)|([1-9]{1}[0-9]*)),(\\+?|-?)(((0\\.|[1-9]{1}[0-9]*\\.)[0-9]+)|(0)|([1-9]{1}[0-9]*))$"

   

    拆分字符串的方法:

String a[] = s.split("\\s");
String b[] = a[i].split(",");

   

    1.第一题解决思路分析:

    第一题功能上只需计算两点间距，设计一个Point类，存放点的横纵坐标，类内定义一个sum计算方法，直接使用数学上的两点间距离公式

len = Math.sqrt(Math.abs((x2-x1)*(x2-x1))+Math.abs((y2-y1)*(y2-y1)));

   

    2.第二题解决思路分析:

    同样设计一个Point类，类里定义题目要求的五种功能对应的五个方法。

    判断三点是否共线有个比较好的思路——先特判斜率不存在的情况，然后任取两点计算斜率，因为必有一点被重复使用，若斜率相等，则说明三点共线。方法三源码如下:

void three(Point point1,Point point2) {
            if(this.x==point1.x&&point1.x==point2.x){
                System.out.println("true");
                return ;
            }
            else if(this.y==point1.y&&point1.y==point2.y){
                System.out.println("true");
                return ;
            }
            double k1 = (this.y - point1.y)/(this.x - point1.x);
            double k2 = (point1.y - point2.y)/(point1.x - point2.x);
            if(k1 == k2) {
                System.out.println("true");
            }
            else {
                System.out.println("false");
            }
        }

   

    方法五需要计算两条直线交点坐标，推出数学公式的过程比较痛苦，个人感觉采取点斜式表示两点构成的直线比采取一般式更清晰明了，点斜式不需要再去计算截距，对于交叉点是否在两条线段之内判断，可以采取用交点坐标与其他所有坐标对比，若交点坐标在线段内，则交点一定被另外四个点包围，可利用Math.max()减少判断条件。方法五源码如下:

void five(Point point1,Point point2,Point point3) {

            double k1 = (this.y - point1.y)/(this.x - point1.x);
            double k2 = (point2.y - point3.y)/(point2.x - point3.x);
            if(k1==k2 ) {
                System.out.println("is parallel lines,have no intersection point");
                return ;
            }
            else {
                double x0 = ((point2.x-point3.x) * (point1.x*this.y - this.x*point1.y) - (this.x-point1.x) * (point3.x*point2.y - point2.x*point3.y)) / ((point2.x-point3.x) * (this.y-point1.y) - (this.x-point1.x) * (point2.y-point3.y));
                double y0 = ((point2.y-point3.y) * (point1.y*this.x - this.y*point1.x) - (this.y-point1.y) * (point3.y*point2.x - point2.y*point3.x)) / ((point2.y-point3.y) * (this.x-point1.x) - (this.y-point1.y) * (point2.x-point3.x));
                System.out.print(x0+","+y0+" ");
                if(x0<Math.max(this.x,Math.max(point1.x,Math.max(point2.x,point3.x)))&&y0<Math.max(this.y,Math.max(point1.y,Math.max(point2.y,point3.y)))&&y0>Math.min(this.y,Math.min(point1.y,Math.min(point2.y,point3.y)))&&x0>Math.min(this.x,Math.min(point1.x,Math.min(point2.x,point3.x)))){
                    System.out.print("true");
                }
                else {
                    System.out.print("false");
                }
            }
        }

 

   3.第三题解题思路分析:

  第三题难度相对较大，总体上还是设计一个Point类，在类里面定义解决相对应问题的方法，前面三个功能相对基础·，只需要判断钝、锐、直三角形和等边、等腰还有重心坐标，相对容易，后面的两个功能比较复杂，老实说，没有什么很好的解题思路。

 

  对于给出三个点，计算该三角形的面积，可以采取先通过三点坐标计算出三角形的三条边，再利用高中学过的海伦公式，使用三条边计算面积，就不再需要计算角度，使程序更简洁。

void two(Point point1, Point point2) {
            double a = Math.sqrt(Math.abs((this.x-point1.x)*(this.x-point1.x))+Math.abs((this.y-point1.y)*(this.y-point1.y)));
            double b = Math.sqrt(Math.abs((this.x-point2.x)*(this.x-point2.x))+Math.abs((this.y-point2.y)*(this.y-point2.y)));
            double c = Math.sqrt(Math.abs((point2.x-point1.x)*(point2.x-point1.x))+Math.abs((point2.y-point1.y)*(point2.y-point1.y)));
            if(!((a + b) > c && ((b + c) > a) && ((a + c) > b))){
                System.out.println("data error");
                return ;
            }
            double C = a+b+c;
            double p = C/2;
            double S = Math.sqrt(p*(p-a)*(p-b)*(p-c));
            double x0 = (this.x+point1.x+point2.x)/3;
            double y0 = (this.y+point1.y+point2.y)/3;
            System.out.printf("%f ",(float)C);
            System.out.printf("%f ",(float)S);
            System.out.printf("%f,",(float)x0);
            System.out.printf("%f",(float)y0);
        }

 

 

• 踩坑心得   

   - 开始并不了解正则表达式，完全按照题目要求一个一个去写判断输入合法的条件，一提交就发现各种问题，包括重复零输入和小数点后无数字等等，反复修改代码，在磕磕绊绊中写完第一题之后才开始了解到正则表达式，只需要一行代码就可以解决全部的输入合法问题，一行抵十几行。

     - 声明对象数组之后，每次使用该对象数组元素时都需要重新new一下，不然其为空。(被这个困扰了很久)

     - 对于浮点型数据，判断三条边是否构成直角三角形时，使用勾股定理不能简单的写成:

if(a*a+b*b==c*c || b*b+c*c==a*a || c*c+a*a==b*b)

       要考虑浮点型数据的误差，可写成:

if(((a==b)&&Math.abs(a*a+b*b-c*c)<1e-6)||((c==a)&&Math.abs(c*c+a*a-b*b)<1e-6)||((c==b)&&Math.abs(c*c+b*b-a*a)<1e-6))

 

• 改进建议

       1. 在定义方法时，需要适当的采取简便方法降低算法的复杂度，完全暴力不光复杂度高，而且代码冗长，可读性差。

 

       2. 添加注释，并不是每次都有充足的时间一次性完成这个程序，若不添加注释，隔了一段时间后再来看自己写的代码，发现都不知道自己在写什么，加上一些注释，方便之后的查阅和修改。 

 

       3. 对代码实现模块化，自顶而下，逐步细化，根据所需要求固定一个大方向，比如设计一个类，再去考虑定义方法一个一个去解决题目的要求。

       4. 尽可能减少代码复用，提高代码质量。

 

• 总结

   ①通过三次大作业，更加理解了java这门语言，熟练了使用java语言来编写程序解决问题，尤其是大作业三，让我对面对对象程序设计初窥门径。

   ②通过大作业三，学到了正则表达式，合理的运用正则表达式能够节省很多不必要的分支判断，提高效率，使代码更加简洁。

   ③也因为三次大作业了解到了许多关于字符串操作方面的方法，如split、substring、charAT等等，对字符串操作更加娴熟。

   ④关于类的设计与类的应用，也有了一个新的层面的认知和经验，这是面对对象的魅力所在。

   ⑤这三次作业，让我的编程能力更进一步，了解到更多不曾知晓或者不够熟悉的知识点，初步形成了面对对象编程的思想。