ABC198_F-Cube

题目链接

Editorial

Ref

题意: 在正方体的六个面各写一个正整数, 求有多少种方案使六个数和为 \(S(6\le S\le10^{18})\).

可以参考下这个 Burnside’s Lemma

法一: Polya 计数定理, 一共 24 种置换, 对骰子, 1 对 6, 2 对 5, 3 对 4.

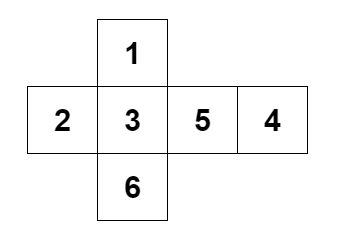
用两个不相交的置换进行打表生成

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>
#include <map>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
typedef long long ll;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;

vector<vector<int> > rot;
map<vector<int>, bool> vis;
int v[10];

vector<int> mul(int x, int y) {
	vector<int> a = rot[x], b = rot[y];
	for (int i = 0; i < 6; ++i) a[i] = b[a[i]-1];
	return a;
}

void print_permu(vector<int> per) {
	memset(v, 0, sizeof(v));
	for (int i = 1; i <= 6; ++i) {
		if (v[i]) continue;
		cout << "(" << i;
		int nxt = per[i-1];
		while (nxt != i) {
			cout << " " << nxt;
			v[nxt] = 1;
			nxt = per[nxt-1];
		}
		cout << ")";
	}
	cout << '\n';
}

int main() 
{
	rot.push_back({4, 2, 1, 6, 5, 3});
	rot.push_back({1, 4, 2, 5, 3, 6});
	vis[rot[0]] = vis[rot[1]] = 1;
	int cnt = 0;
	while (++cnt <= (int)rot.size()) {
		print_permu(rot[cnt-1]);
		vector<int> nxt;
		for (int i = 0; i < cnt - 1; ++i) {
			if (!vis[nxt = mul(cnt - 1, i)]) {
				vis[nxt] = true;
				rot.push_back(nxt);
			}
		}
	}
	cout << cnt - 1 << '\n';
    return 0;
}

得到如下结果

(1 4 6 3)(2)(5)
(1)(2 4 5 3)(6)
(1 4 5)(2 6 3)
(1 6)(2 3)(4 5)
(1 5)(2 6)(3 4)
(1 3 2)(4 5 6)
(1 6)(2)(3 4)(5)
(1 3 6 4)(2)(5)
(1 5 4)(2 3 6)
(1 3 5)(2 6 4)
(1)(2 3 5 4)(6)
(1 4 2)(3 5 6)
(1 2)(3 4)(5 6)
(1 2 4)(3 6 5)
(1 2 6 5)(3)(4)
(1 4)(2 5)(3 6)
(1 6)(2 4)(3 5)
(1)(2)(3)(4)(5)(6)
(1 2 3)(4 6 5)
(1 5 6 2)(3)(4)
(1 5 3)(2 4 6)
(1 3)(2 5)(4 6)
(1)(2 5)(3 4)(6)
(1 6)(2 5)(3)(4)
24

为方便计算, S 减去 6 限制变为非负整数, 可以看到

• a+b+c+d+e+f=S, 1种
  • \(\begin{pmatrix}S+5\\5\end{pmatrix}\)
• a+b+2c+2d=S, 3种
  • 记 \(tmp=\lfloor S/2\rfloor\), \(c+d=k,a+b=S-2k\),推导如下

\[\begin{array}{c}\displaystyle\displaystyle\sum_{k=0}^{tmp}(k+1)(S-2k+1)&=&\displaystyle\sum_{k=0}^{tmp}\left[(S+1)(k+1)-2k^2-2k\right]\\ &=&\displaystyle(S+1)\frac{(tmp+1)(tmp+2)}{2}-2\frac{tmp(tmp+1)(2tmp+1)}{6}-tmp(tmp+1)\\ &=&\displaystyle\frac{(tmp+1)(tmp+2)(3S-4tmp+3)}{6}\end{array}\]

• a+b+4c=S, 6种
  • 记 \(tmp=\lfloor S/4\rfloor\), \(\displaystyle\sum_{c=0}^{tmp}\begin{pmatrix}S-4c+1\\1\end{pmatrix}=(tmp+1)\cdot (S+1)-2\cdot tmp(tmp+1)=(tmp+1)\cdot(S-2tmp+1)\)
• 2a+2b+2c=S, 6种
  • \(\begin{pmatrix}\frac{S}{2}+2\\2\end{pmatrix}\)
• 3a+3b=S, 8种
  • \(\begin{pmatrix}\frac{S}{3}+1\\1\end{pmatrix}=\frac{S}{3}+1\)

  有一个结论是 \(c_1x_1+c_2x_2+\cdots c_nx_n=S(l_i\le x_i\le r_i)\) 的解的个数是生成函数 \(G(y)=\left(y^{c_1l_1}+\cdots y^{c_1r_1}\right)\cdots\left(y^{c_nl_n}+\cdots y^{c_nr_n}\right)\) 展开后 \(y^S\) 的系数.

---

• 不旋转, 1 种
• 转轴为垂直面的中心(3条), \(90,270\) 度, \(3\times2=6\) 种
• 转轴为垂直面的中心连线(3条), \(180\) 度, 3 种
• 转轴为对棱中心连线(6条), \(180\) 度, 6 种
• 转轴为体对角线(4条), \(120,240\) 度, \(4\times2=8\) 种

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
typedef pair<int, int> pii;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const ll MOD = 998244353;

ll S, ans;

ll qpow(ll a, ll x) {
	ll res = 1;
	for (; x; x >>= 1, (a *= a) %= MOD)
		if (x & 1) (res *= a) %= MOD;
	return res; 
}

ll C(int n, int m) { // 
	if (m > n) return 0;
	ll res = 1;
	for (int i = n; i >= n - m + 1; --i) (res *= i) %= MOD;
	for (int i = 2; i <= m; ++i) (res *= qpow(i, MOD - 2)) %= MOD;
	return res;
}

int main() 
{
	cin >> S; S -= 6;
	ll res, tmp;
	// a+b+c+d+e+f=S
	res = C((S + 5) % MOD, 5);
	(ans += res) %= MOD; // debug(res);

	// a+b+2c+2d=S
	tmp = S / 2 % MOD;
    res = (tmp + 1) * (tmp + 2) % MOD * (3 * S % MOD - 4 * tmp + 3) % MOD * qpow(6, MOD - 2) % MOD; 
	(ans += 3 * res) %= MOD; // debug(res);

	// a+b+4c=S
	tmp = S / 4 % MOD;
	res = (tmp + 1) * (S % MOD - 2 * tmp + 1) % MOD;
	(ans += 6 * res) %= MOD; // debug(res);

	// 2a+2b+2c=S
	if (S % 2 == 0) {
		res = C((S / 2 + 2) % MOD, 2);
		(ans += 6 * res) %= MOD; // debug(res);
	}

	// 3a+3b=S
	if (S % 3 == 0) {
		res = (S / 3 + 1) % MOD;
		(ans += 8 * res) %= MOD; // debug(res);
	}

	// debug(ans);
	(ans *= qpow(24, MOD - 2)) %= MOD;

	cout << (ans + MOD) % MOD << '\n';
    return 0;
}

法三: OEIS(A054473)