莫队

考虑一个这样的问题：

给定一个长度为 \(n\) 的序列 \(a\)。\(q\) 次静态询问。每次给定一个区间 \(l, r\)，求解这个区间的某种属性。允许离线。

一般来说暴力做复杂度是 \(\mathcal O(nq)\) 甚至更高的。比如说如果要求解区间颜色数（即有多少种不同的数），那么需要维护一个桶统计每种数字的出现次数。然后维护一个指针，从 \(l\) 往 \(r\) 扫描，每扫到一个数就更新桶，并尝试更新答案。

int cnt[N], res;

for (int i = l; i <= r; ++ i ) {
    if (!cnt[a[i]]) res ++ ;
    cnt[a[i]] ++ ;
}

这个“扫描”的过程可以这样理解：如果我们已经解决了 \([l, r]\) 的询问，维护好了统计每个数字的出现次数的桶，那么我们可以用 \(\mathcal O(1)\) 的时间复杂度更新表示 \([l, r+1]\) 的桶，以及求解 \([l, r+1]\) 的答案。

同理，如果已经处理好了 \([l, r]\) 的询问，那么 \([l, r\pm 1],[l \pm 1, r]\) 也可以 \(\mathcal O(1)\) 的更新桶、求答案。

那么如果上一次询问的区间是 \([l, r]\)，下一次询问的区间是 \([l',r']\)，那么我们可以用上面的方法，每次让一个端点加减 \(1\)，就可以在 \(|l-l'|+|r-r'|\) 步内得到新的答案。

事实上，如果我们把一次 \([l, r]\) 的询问看作是平面上 \((l, r)\) 这个点，那么从上一次询问 \([l, r]\) 拓展到下一次询问 \([l', r']\) 的复杂度，就等于平面上 \((l, r)\) 和 \((l', r')\) 的曼哈顿距离。

显然截至目前我们并没有将复杂度从暴力的 \(\mathcal O(nq)\) 优化下来，因为任意两个点的曼哈顿距离都是 \(\mathcal O(n)\) 级别的。但是注意到询问允许离线，也就是我们可以任意调换处理询问的顺序。那么是否存在一种处理询问的顺序使得可以证明它的复杂度小于 \(\mathcal O(nq)\) 呢？

现在的问题是：

平面上有 \(q\) 个点，每个点横纵坐标都在 \([1, n]\) 内。现在要求从某个点开始游走，要求遍历到每个点，且走的总距离（也就是每相邻两个点的曼哈顿距离）最小。

第一个想法是，如果所有点的纵坐标都随横坐标的增大而增大，那么我们只需要从横纵坐标最小的那个点出发，一直向右或向上走。这样总共向上走 \(\mathcal O(n)\) 次，向右走 \(\mathcal O(n)\) 次，总复杂度就是 \(\mathcal O(n)\) 的。事实上这就是双指针的思想。

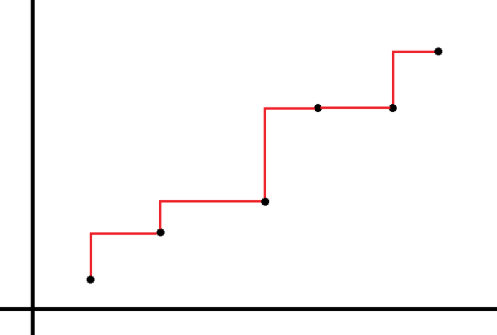
显然题目并没有保证这个优美的性质。于是我们考虑将点分成若干组，每组内尽量满足这个性质。

分组的方法是这样的：我们将横坐标（对应回区间就是左端点）接近的点分成一组。具体的，我们设置一个阈值 \(B\)，将横坐标在 \([1,B]\) 内的点分在同一组，在 \([B+1,2B]\) 内的点分在同一组，在 \([2B+1,3B]\) 内的点分在同一组，以此类推。显然所有点被分成了 \(\mathcal O(\dfrac qB)\) 个组。

然后我们将组内的点按照纵坐标（对应会区间就是右端点）从小到大排序，即按照纵坐标从小到大遍历每个点，也即每个组内只往上走不往下走。

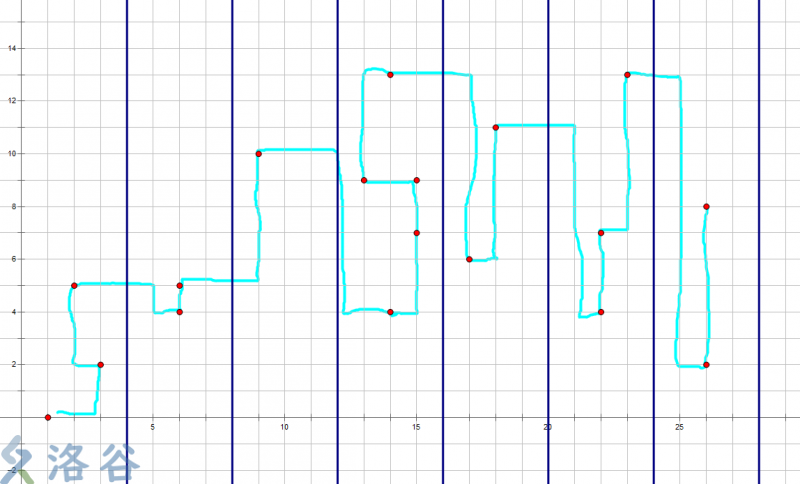
from Gu_Pigeon.

这样虽然也没法在组内实现「所有点的纵坐标都随横坐标的增大而增大」，但是每当下一个点的横坐标出现问题（即这个点的横坐标比上一个点的横坐标大）时，我们也只需要用 \(\mathcal O(B)\) 步就能解决。感觉上复杂度是很优秀的。

具体地我们分析这个做法也就是莫队算法的复杂度。分为四个方面：向上/下/左/右分别走的步数。

我们知道每个组内一定只向上走，而一个组内最低和最高点的纵坐标之差是 \(\mathcal O(n)\) 的，于是向上走的步数为 \(\mathcal O(\dfrac qB\times n)\)。

而向下走只会出现在组与组之间，仍然是 \(\mathcal O(\dfrac qB \times n)\)。

一个组内的任意时刻都可能会向左或向右走以到达下一个点，但是如果想要不出组就至多走 \(B\) 步。于是组内向左或向右走的总步数为 \(\mathcal O(q B)\)。

而如果想从当前组走到下一个组，显然左右只会走至多 \(2B\) 步，于是这种情况的总步数为 \(\mathcal O(\dfrac qB \times B)\)。

于是总复杂度就是 \(\mathcal O(\dfrac qB \times n + \dfrac qB \times n + qB + \dfrac qB \times B) = \mathcal O(\dfrac qB \times n + qB)\)。

注意到 \(\dfrac qB \times n + qB = q (\dfrac nB+B)\)，而根据均值不等式 \(\dfrac nB +B \ge 2\sqrt n\)，所以当 \(B=\sqrt n\) 时，复杂度达到最小值 \(\mathcal O(q \sqrt n)\)。