陨石的秘密 ⭐
题面
公元11380年,一颗巨大的陨石坠落在南极。
于是,灾难降临了,地球上出现了一系列反常的现象。
当人们焦急万分的时候,一支中国科学家组成的南极考察队赶到了出事地点。
经过一番侦察,科学家们发现陨石上刻有若干行密文,每一行都包含5个整数:
1 1 1 1 6
0 0 6 3 57
8 0 11 3 2845
著名的科学家SS发现,这些密文实际上是一种复杂运算的结果。
为了便于大家理解这种运算,他定义了一种SS表达式:
1. SS表达式是仅由’{‘,’}’,’[‘,’]’,’(’,’)’组成的字符串。
2. 一个空串是SS表达式。
3. 如果A是SS表达式,且A中不含字符’{‘,’}’,’[‘,’]’,则(A)是SS表达式。
4. 如果A是SS表达式,且A中不含字符’{‘,’}’,则[A]是SS表达式。
5. 如果A是SS表达式,则{A}是SS表达式。
6. 如果A和B都是SS表达式,则AB也是SS表达式。
例如
()(())[]
{()[()]}
{{[[(())]]}}
都是SS表达式。
而
()([])()
[()
不是SS表达式。
一个SS表达式E的深度D(E)定义如下:

例如(){()}[]的深度为2。
密文中的复杂运算是这样进行的:
设密文中每行前4个数依次为L1,L2,L3,D,求出所有深度为D,含有L1对{},L2对[],L3对()的SS串的个数,并用这个数对当前的年份11380求余数,这个余数就是密文中每行的第5个数,我们称之为神秘数。
密文中某些行的第五个数已经模糊不清,而这些数字正是揭开陨石秘密的钥匙。
现在科学家们聘请你来计算这个神秘数。
输入格式
共一行,4个整数 L1,L2,L3,D。
输出格式
共一行,包含一个整数,即神秘数。
数据范围
0≤L1,L2,L3≤10,
0≤D≤30
输入样例:
1 1 1 2
输出样例:
8
题解
先想到 f[d][i][j][k] 表示深度为d, i个{}, j个[], k个()的方案数
添加括号转移很简单,但是
对于 相同深度不好转移比如
f[d][i][j][k] += f[d][i - ii][j - jj][k - kk] + f[d][ii][jj][kk]
这个转移的重复问题很难解决,
eg: {}[]() + {}[]() == {} + [](){}[]() == {}[] + (){}[]()
发现重复了三次,如果更长的串呢?重复很难解决
那么干脆通过前缀和思想来解
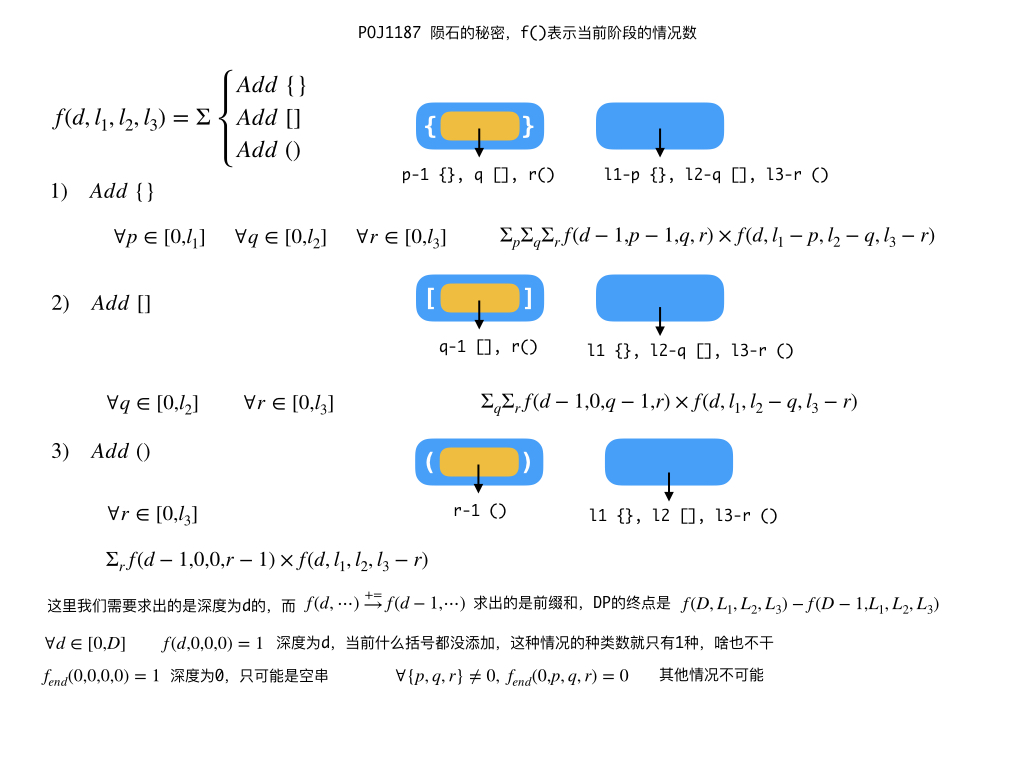
f[d][i][j][k] 表示深度 小于等于 d, i个{}, j个[], k个()的方案数
那么f[d][a][b][c] - f[d - 1][a][b][c]即为所求
怎么转移从f[d-1]到f[d]呢? f[d - 1] (加括号) * f[d] (拼接)即可 (所以f[0~d][0][0][0]初始化为1)
详细看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 11380;
ll f[31][11][11][11];
int a, b, c, d;
int main()
{
cin >> a >> b >> c >> d;
for (int i = 0; i <= d; ++i) f[i][0][0][0] = 1;
for (int D = 1; D <= d; ++D)
for (int A = 0; A <= a; ++A)
for (int B = 0; B <= b; ++B)
for (int C = 0; C <= c; ++C)
{
ll& sum = f[D][A][B][C];
for (int aa = 1; aa <= A; ++aa)
for (int bb = 0; bb<= B; ++bb)
for (int cc = 0; cc <= C; ++cc)
sum = (sum + (f[D - 1][aa - 1][bb][cc] * f[D][A - aa][B - bb][C - cc]) % mod) % mod;
for (int bb = 1; bb <= B; ++bb)
for (int cc = 0; cc <= C; ++cc)
sum = (sum + (f[D - 1][0][bb - 1][cc] * f[D][A][B - bb][C -cc]) % mod) % mod;
for (int cc = 1; cc <= C; ++cc)
sum = (sum + (f[D - 1][0][0][cc - 1] * f[D][A][B][C -cc]) % mod) % mod;
}
cout << (f[d][a][b][c] - (d ? f[d - 1][a][b][c] : 0) + mod) % mod;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号