CF杂题乱写 5

213C Ralay Race

这个题和方格取数传纸条是一个模型
定义\(f_{i,j,k}\)为走\(i\)步，横坐标分别\(j,k\)的经过点权和
状态转移就非常好转了：

f[k][i][j]=max(f[k][i][j],f[k-1][i][j]+t);
f[k][i][j]=max(f[k][i][j],f[k-1][i-1][j]+t);
f[k][i][j]=max(f[k][i][j],f[k-1][i][j-1]+t);
f[k][i][j]=max(f[k][i][j],f[k-1][i-1][j-1]+t);

实际上对应可能有点问题但是不影响阅读
然后\(t\)就是当前这一步决策的价值，注意去重
就有

if(i==j) t=a[i][k-i+1];
else t=a[i][k-i+1]+a[j][k-j+1];

837D Round Subset

每个后缀\(0\)都可以看做\(2\cdot 5\)
直接\(DP\)不好搞，解决这种问题考虑泛化背包
于是这种就是二维背包
考虑第二维价格为质因数分解中\(2/5\)的指数
优化内存用\(5\)的
最后选够\(k\)个，答案就是\(max(min(w_i,v_i)),\)

540D Bad Luck Island

显然就是以三种人为状态的定义
设\(f_{i,j,k}\)为三种人分别剩下的人数
那么对于相遇的总数不难通过乘法原理写出：
\(tot=i\cdot j+j\cdot k+k\cdot i\)
对于一个人被杀死的情况，由于人没有区别，
所以还是一个乘法原理，分别是
\(i\cdot j ,\space j\cdot k,\space k\cdot i\)
于是状态转移就比较好写了，
少一个人的局面就加上(现在的局面概率\(\times\)转移的概率)

now=i*j+j*k+k*i;
if(i&&k)f[i-1][j][k]+=f[i][j][k]*(1.0*k*i)/now;
if(i&&j)f[i][j-1][k]+=f[i][j][k]*(1.0*j*i)/now;
if(k&&j)f[i][j][k-1]+=f[i][j][k]*(1.0*j*k)/now;

478D Red-Green Towers

实际上塔高\(\Theta(\sqrt{n})\)
剩下的部分当成背包方案转移即可

505C Mr. Kitayuta, the Treasure Hunter

状态转移方程实际上非常好写
定义\(f_{i,j}\)为到\(i\)上一步跳\(j\)的最多宝藏数
于是就是当前状态=上一步的最多+这个点的数
但是有个问题\(j\)开多大
实际上这还是个等差数列，所以\(\Theta\sqrt{n}\)就够了

1265E Beautiful Mirrors

期望套路，
显然要设\(f_i\)照到\(i\)以后的期望步数
然后考虑从哪转移
如果成功，就是到\(f_{i+1}\)否则\(f_1\)
这一步反正都得走，于是状态转移：
\(f_i=p_i\cdot f_{i+1}+(1-p_i)\cdot f_{1}+1\)
初值\(f_{n+1}=0,\)目标\(f_1\)
常规反解即可

16E Fish

概率状压\(DP\)
注意到\(n\)其实很小，而每条鱼生死不可混淆
所以二进制下第\(i\)位表示\(i\)条是否活着
\(0\)死\(1\)活
钦定\(i\)这个局面是从\(i\space or\space {2^j}\)转移而来
然后\(j\)是被\(k\)这条鱼杀死的
很容易知道总相遇数就是\(C_{now}^2,now\)是所有存活数
那么当前局面加上钦定局面概率乘上\(p_{k,j}\)再乘上相遇概率(1/相遇数)
初值\(f_{2^n-1}=1.0\)，目标\(f_{2^i},i\in[0,n-1]\)

621E Wet Shark And Blocks

常规技巧：
开桶处理小模数下每个数的出现次数，于是就和\(n\)无关了
首先带着\(b\)这一维列个状态：
\(f_{i,j}\)就是在\(i\)格取数然后取模后是\(j\)的方案数
状态转移方程很好写：
\(f_{i+1,10\cdot j+k\bmod x}+=f_{i,j}\cdot a_{k},a_k\)是出现次数
实际上我们不可能把\(b\)直接扔进去，
这种情况下考虑矩阵加速递推即可

235B Let's Play OSU!

实际上这种问题维护每次增量即可

y=y*(1-p)+p*(y+x*2+1);
x=p*(x+1);

734E Anton and Tree

颜色相同联通块不好搞，但是单点修改非常好搞
考虑如何修改为单点操作，联通块到点不难想到缩点
于是第一步缩点，用并查集对于颜色相同的直连点合并
这样新树上一个点就对应原图上一个颜色相同的联通块
同时，类似广义圆方树的，有
任意一条边的两个端点颜色不同
因为每一个并查集的联通块都是极大的

新树上一个错误的做法就是分层染色
事实上我们可以构造一个更优的操作：
把这一个点染成下一层颜色，再把所有颜色染回去
两步构造一层
莫名想到《三体》里先把自己改造成二维生物再降维打击
这样操作一定优，见图：

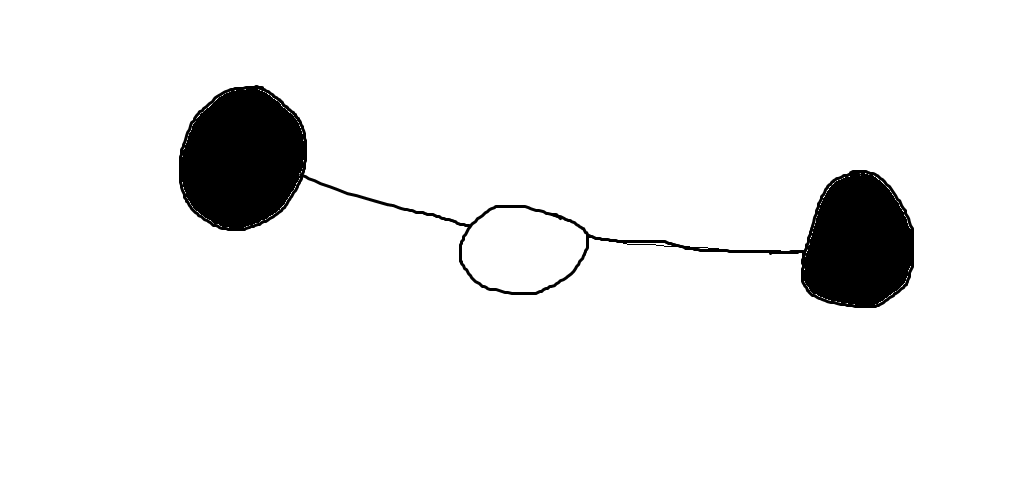
染一层是\(2\)步
而这时

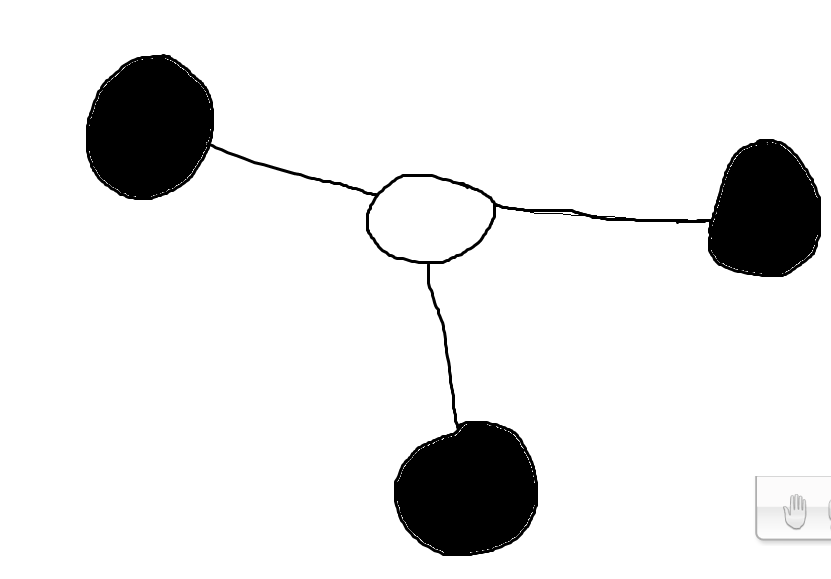
染一层是\(3\)步
(省略其他节点)
钦定这个是直径中点，于是无论如何上述两步构造总会更优
对于接下来情况重复缩点-染色过程即可
显然通过这种构造方法，最少步数：（新树直径+1）/2