力扣474、一和零动态规划

解法1：复杂度很高

import numpy as np
class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        strNumber = len(strs)
        dp = np.zeros((strNumber+1,m+1,n+1),dtype=int)
        for i in range(1,strNumber+1):
            temp=strs[i-1]
            count = [0,0]
            # 计算0和1的个数
            for l in range(len(temp)):
                if temp[l]=='0':
                    count[0] +=1
                else:
                    count[1] +=1
            for j in range(m+1):
                for k in range(n+1):
                    if count[0]>j or count[1]>k:
                        dp[i][j][k] = dp[i-1][j][k]
                    else:
                        dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-count[0]][k-count[1]]+1)
        return int(dp[strNumber][m][n])

优化1

        利用count函数优化一下求字符个数哪儿

import numpy as np
class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        strNumber = len(strs)
        dp = np.zeros((strNumber+1,m+1,n+1),dtype=int)
        for i in range(1,strNumber+1):
            temp=strs[i-1]
            count = [0,0]
            # 计算0和1的个数
            count[0] = temp.count("0")
            count[1] = temp.count("1")
            for j in range(m+1):
                for k in range(n+1):
                    if count[0]>j or count[1]>k:
                        dp[i][j][k] = dp[i-1][j][k]
                    else:
                        dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-count[0]][k-count[1]]+1)
        return int(dp[strNumber][m][n])

优化2

        参考01背包里面二维变一维，这儿可以三维变二维

import numpy as np
class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        strNumber = len(strs)
        dp = np.zeros((m+1,n+1),dtype=int)
        for i in range(1,strNumber+1):
            temp=strs[i-1]
            count = [0,0]
            # 计算0和1的个数
            count[0] = temp.count("0")
            count[1] = temp.count("1")
            for j in range(m,count[0]-1,-1):
                for k in range(n,count[1]-1,-1):
                    dp[j][k] = max(dp[j][k],dp[j-count[0]][k-count[1]]+1)
        return int(dp[m][n])

or

import numpy as np
class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        strNumber = len(strs)
        dp = np.zeros((m+1,n+1),dtype=int)
        for str_item in strs:
            count = [0,0]
            # 计算0和1的个数
            count[0] = str_item.count("0")
            count[1] = str_item.count("1")
            for j in range(m,count[0]-1,-1):
                for k in range(n,count[1]-1,-1):
                    dp[j][k] = max(dp[j][k],dp[j-count[0]][k-count[1]]+1)
        return int(dp[m][n])

       

                可惜以上版本提交的时候都超时

               

优化3

        原因在于我的初始化用了numpy，我找了好久，发现是这问题，懵逼。

class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        if len(strs) == 0:
            return 0
        dp = [[0] * (n+1) for _ in range(m+1)]
        for str_item in strs:
            count=[0,0]
            count[0] = str_item.count("0")
            count[1] = str_item.count("1")
            for i in range(m, count[0] - 1, -1):
                for j in range(n, count[1] - 1, -1):
                    dp[i][j] = max(dp[i][j], dp[i-count[0]][j-count[1]]+1)
        return dp[m][n]

        这个就可以提交通过了

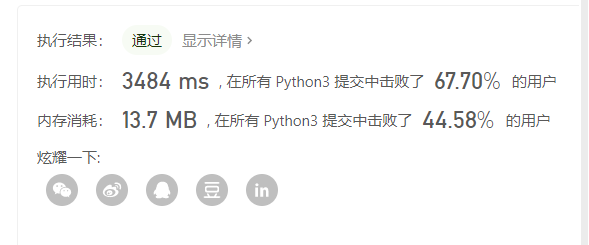
c++版本

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int strNumber = strs.size();
        int dp[strNumber+1][m+1][n+1];
        memset(dp, 0, sizeof(dp));   //初始化
        for (int i =1;i<=strNumber;++i){
            string str =strs[i-1];
            int count[2]={0,0};  // 初始化
            for(int i=0;i<str.size();++i){
                if(str[i]=='0')
                    count[0] += 1;
                else 
                    count[1] += 1;
            }
            for (int j=0;j<=m;++j){
                for(int k=0;k<=n;++k){
                    if(count[0]<=j&&count[1]<=k){
                        dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-count[0]][k-count[1]]+1);
                    }
                    else
                        dp[i][j][k]= dp[i-1][j][k];
                }
            }
        } 
        return dp[strNumber][m][n];
    }
    int max(int a,int b){
        return a>b?a:b;
    }
};

        给了一个初始版本的，可以慢慢按照python的优化思路一步步来，哪怕是是这个三维数组的c++，人家都没超时，提交都通过了，python着实有点慢