数据结构--二叉堆

二叉堆是完全二元树或者是近似完全二元树，按照数据的排列方式可以分为两种：最大堆和最小堆。
最大堆：父结点的键值总是大于或等于任何一个子节点的键值；最小堆：父结点的键值总是小于或等于任何一个子节点的键值。示意图如下：

 

二叉堆一般都通过"数组"来实现。数组实现的二叉堆，父节点和子节点的位置存在一定的关系。有时候，我们将"二叉堆的第一个元素"放在数组索引0的位置，有时候放在1的位置。当然，它们的本质一样(都是二叉堆)，只是实现上稍微有一丁点区别。
假设"第一个元素"在数组中的索引为 0 的话，则父节点和子节点的位置关系如下：
(01) 索引为i的左孩子的索引是 (2*i+1);
(02) 索引为i的右孩子的索引是 (2*i+2);
(03) 索引为i的父结点的索引是 floor((i-1)/2);

 

 

 

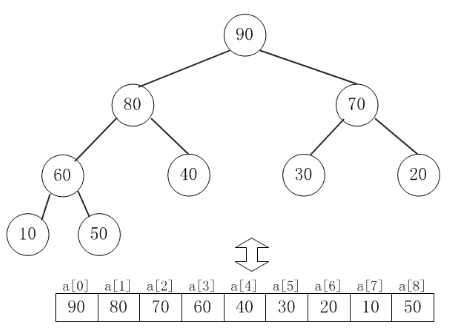
假设"第一个元素"在数组中的索引为 1 的话，则父节点和子节点的位置关系如下：
(01) 索引为i的左孩子的索引是 (2*i);
(02) 索引为i的右孩子的索引是 (2*i+1);
(03) 索引为i的父结点的索引是 floor(i/2);

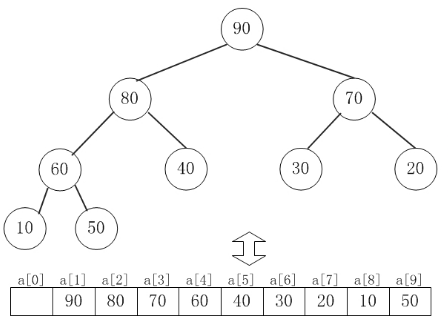
二、二叉堆的操作

堆一般使用数组来构建，假设为数组a[]，结点通常存储在a[1]，这样对于下标为k的结点a[k]来说，其左孩子的下标为2*k，右孩子的下标为2*k+1。

1、插入结点到堆中.

由于小根堆是由数组实现的完全二叉树，所以插入的位置应该是完全二叉树的最后一个位置（如下图所示），对于小根堆来讲，需要满足两个性质：（1）堆为完全二叉树；（2）堆中每个结点的值都不大于其左右结点的值。插入结点可能会破坏这两条性质，所以在插入结点后需要对堆进行调整。调整方法为：将插入的结点与其父结点比较，若小于其父结点的值，则交换两者。重复此操作，直至该结点不比其父结点小，或者该结点成为根结点。可以通过插入结点到一个已经存在的堆中，也可以通过不断插入结点来构建一个堆。

 

 

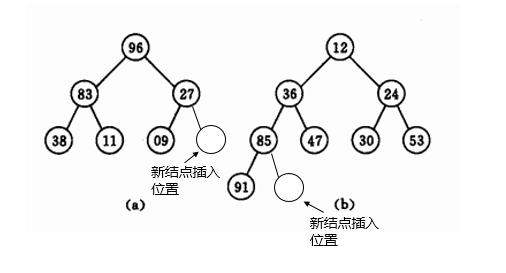
2、删除堆顶元素（堆排序）

删除堆顶元素（根结点）后，会得到左右两棵子树，此时将堆中最后一个元素移到堆顶，然后自上而下调整，将该结点与左右孩子结点比较，此时会有三种情况：

（1）结点的左右孩子均为空，此时调整结束；

（2）结点只有左孩子，此时将该结点与其左孩子比较。若结点大于其左孩子，则两者交换，否则调整结束；

（3）结点左右孩子都非空，则将该结点与左右孩子之间的较小者比较，若小于则交换，否则调整结束；

重复此过程，直到该结点不大于其左右孩子结点，或者该结点为叶子结点。

/*
对于二叉堆，介绍以下几种操作：
插入节点；
上浮节点；
删除节点；
下沉节点；
构建二叉堆；
C++中的STL库中可以实现，这一功能简化了自己手写模板的麻烦，增加了运用的方便。

例如一个程序：

就可以实现对于二叉堆挥着队列中的元素进行排序选择最大的元素。

 #include <iostream>
 #include <queue>
 #include <algorithm>
 using namespace std;
 priority_queue<int> q;
 int main()
 {
 q.push(1);
 q.push(2);
 q.push(3);
 cout<<q.top()<<endl;
 return 0;
 }

 那么这么好用的东西，那么细致学习一下。


 对于优先队列有几个基本的操作：

 empty() 如果队列为空返回真
 pop() 删除对顶元素
 push() 加入一个元素
 size() 返回优先队列中拥有的元素个数
 top() 返回优先队列对顶元素

 在int类型中默认的是大顶堆， 也就是top（）处来的第一个元素是队列中最大的。

 使用方法：
 头文件：

 #include <queue>
 声明方式：

 1、普通方法：

 priority_queue<int> q; //q表示的是队列的名字
 //简单使用
 #include <iostream>
 #include <queue>
 #include <algorithm>
 using namespace std;
 priority_queue<int> q;
 int main()
 {
 q.push(1);
 q.push(2);
 q.push(3);
 cout<<q.top()<<endl;
 return 0;
 }




 //自己定义结构体
 //最小值优先， x小的优先级高
 //声明是
 priority_queue<int, vector<int>, cmp> q;
 //第一个是优先队列的类型， 第二个为容器的类型， 第三个是标胶函数

 //小顶堆
 struct cmp
 {
 bool operator()(int x, int y)
 {
 return x > y;
 }
 };

 //大顶堆
 struct cmp
 {
 bool operator()(int x, int y)
 {
 return y > x;

 }
 };

 2、优先级定义


 //例如下面的程序
 #include <iostream>
 #include <algorithm>
 #include <queue>
 using namespace std;
 struct cmp
 {
 bool operator()(int x, int y)
 {
 return y > x;
 }

 };

 int main()
 {
 priority_queue<int, vector<int>, cmp> q;
 q.push(1);
 q.push(51);
 q.push(12);
 q.push(331);
 q.push(12);
 cout<<q.top()<<endl;
 return 0;
 }

 3、结构体声明方式：
 //定义方法：
 prioritry_queue<node >q;

 //结构体中，x小的优先级高
 struct node
 {
 int x, y;
 friend bool operator < (node a, node b)
 {
 return a.x > b.x;

 }
 };


*/
#include <algorithm>
#include <iostream>
using namespace std;
class MinHeap
{
private:
	int* heap;        //存储堆
	int cur;          //堆中结点个数
	/*插入结点后，向上调整*/
	void adjustUp();

	/*删除结点后，向下调整*/
	void adjustDown(int idx);
public:
	MinHeap();
	~MinHeap();
	/*插入值为val的结点*/
	void insert(int val);
	/*返回最小值并删除最小值结点*/
	int deleteMin();
};

MinHeap::MinHeap()
{
	heap = new int[20];
	cur = 0;
}

MinHeap::~MinHeap()
{
	delete[] heap;
}

/*插入值为val的结点*/
void MinHeap::insert(int val)
{
	heap[++cur] = val;
	adjustUp();
}

/*插入结点后，向上调整*/
void MinHeap::adjustUp()
{
	int idx = cur;
	int pIdx = cur / 2;
	while (pIdx > 0 && heap[idx] < heap[pIdx])
	{
		swap(heap[idx], heap[pIdx]);
		idx = pIdx;
		pIdx = pIdx / 2;
	}
}
/*返回最小值并删除最小值结点*/
int MinHeap::deleteMin()
{
	int minVal = heap[1];
	heap[1] = heap[cur--];
	adjustDown(1);
	return minVal;
}

/*删除结点后，向下调整*/
void MinHeap::adjustDown(int idx)
{
	if (idx > cur)
		return;
	int lIdx = idx * 2;
	int rIdx = idx * 2 + 1;

	int minIdx = 0;
	if (lIdx > cur)            //无左右孩子
		return;
	else if (rIdx > cur)       //只有左孩子
		minIdx = lIdx;
	else minIdx = heap[lIdx] < heap[rIdx] ? lIdx : rIdx;    //左右孩子均非空

	if (heap[idx] > heap[minIdx])
	{
		swap(heap[idx], heap[minIdx]);
		adjustDown(minIdx);
	}
	else return;
}

int main()
{
	int a[] = { 5, 1, 3, 4, 2 };
	int len = sizeof(a) / sizeof(a[0]);

	/*插入结点构造最小堆*/
	MinHeap* minHeap = new MinHeap();
	for (int i = 0; i < len; i++)
		minHeap->insert(a[i]);

	/*输出堆顶结点的值*/
	for (int i = 0; i < len; i++)
		cout << minHeap->deleteMin() << " ";
	cout << endl;

	return 0;
}