数据结构--二叉查找树

二叉查找树(Binary Search Tree)，又被称为二叉搜索树。
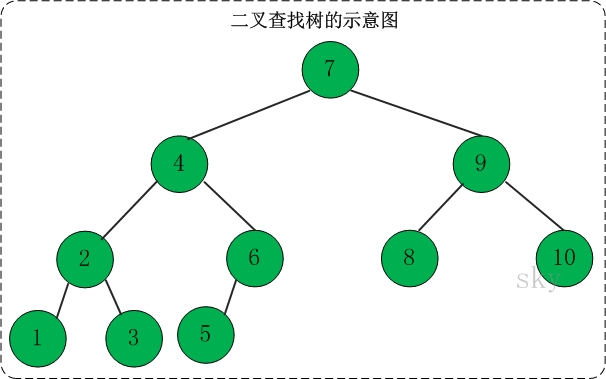
它是特殊的二叉树：对于二叉树，假设x为二叉树中的任意一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。那么，这棵树就是二叉查找树。如下图所示：

在二叉查找树中：
(01) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
(02) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点（no duplicate nodes）。

 

查找节点：

若二叉查找树为空，则查找失败
若该树非空且查找数据x等于根节点的值，则查找成功，返回根节点
若该树非空且查找数据x小于根节点的值，则查找左子树，直到值相等，并返回节点
若该树非空且查找数据x大于根节点的值，则查找右子树，直到值相等，并返回节点
插入节点：

若二叉查找树为空，则将结点作为根节点插入
若所插入节点关键字值等于根节点的值，则插入失败，并返回
若所插入节点关键字值小于根节点的值，则把节点插入到左子树中
若所插入节点关键字值大于根节点的值，则把节点插入到右子树中
删除节点：

若p结点为叶子结点，则删去该叶子结点，修改其双亲结点的指针即可。
若p结点只有左子树PL或右子树PR，此时只要令PL或PR直接成为其双亲结点的左子树（当p是左子树）或右子树（当p是右子树）。
若p结点的左子树和右子树均不空。找出节点p的后继节点y（一定在节点p的右子树中），以右子树中的最小数作为后继节点。

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#define LENGTH 11
struct BinSearNode
{
	int key;
	struct BinSearNode *left_child;
	struct BinSearNode *right_child;
	struct BinSearNode *parent;
}Node;
typedef struct BinSearNode *PNode;
/*Search the node of the tree*/
PNode Search_Tree(PNode root, int key)
{
	PNode x = root;
	//the tree is not empty and the key is not equal
	while (NULL != x && x->key != key)
	{
		if (x->key<key)
			x = x->right_child;//along the right child of tree,until it is empty
		else
			x = x->left_child;//along the left child of tree,until it is empty
	}
	return x;//return the node
}
/*the minimum key of node in the tree*/
PNode Minimum_Tree(PNode root)
{
	PNode x = root;
	while (NULL != x->left_child)
	{
		x = x->left_child;
	}
	return x;
}
/*the maxmum key of node in the tree*/
PNode Maxmum_Tree(PNode root)
{
	PNode x = root;
	while (NULL != x->right_child)
	{
		x = x->right_child;
	}
	return x;
}
/*the successor node of the x,后继节点可以这么理解，将查找树从小到大排序，比他大的值
如果有右孩子，那么应该是右子树当中的最小值
如果没有右孩子，那么应该向上追溯，直至一个分支节点是其父节点的左孩子，返回父节点
可以用于operate++*/
PNode Successor_Tree(PNode x)
{
	PNode y = NULL;
	//case 1:the right subtree of node x is not empty
	if (NULL != x->right_child)
	{
		y = Minimum_Tree(x->right_child);
	}
	//case 2:the right subtree of node x is empty
	//and the node of x has a successor node y
	else
	{
		y = x->parent;
		while (NULL != y && x == y->right_child)
		{
			x = y;
			y = y->parent;
		}
	}
	return y;
}
/*the predecessor node of the x，前任节点
如果节点有左孩子，那么找到左孩子的最大值
如果没有左孩子，那么向上追溯直至一个分支当前节点是对应父节点的右孩子，返回父节点的值
*/
PNode Predecessor_Tree(PNode x)
{
	PNode y = NULL;
	//case 1:the left subtree of node x is not empty
	if (NULL != x->left_child)
	{
		y = Maxmum_Tree(x->left_child);
	}
	//case 2:the left subtree of node x is empty
	//and the node of x has a predecessor node y
	else
	{
		y = x->parent;
		while (NULL != y && x == y->left_child)
		{
			x = y;
			y = y->parent;
		}
	}
	return y;
}

/*insert a new node into the BST*/
void Insert_Tree(PNode *root, int key)
{
	PNode x = *root;
	PNode y = NULL;
	PNode z = (PNode)malloc(sizeof(Node));//<开辟一个节点的空间
	if (NULL == z)
	{
		printf("malloc the z is failed.");
		exit(1);
	}
	//initial the node of z
	z->key = key;
	z->left_child = z->right_child = z->parent = NULL;
	//Find the location node of y to insert the node of z
	while (NULL != x)
	{
		y = x; //<找到当前树满足条件的叶子节点了，表示为y，之后在y节点后面进行插入操作
		if (z->key<x->key)
			x = x->left_child;
		else
			x = x->right_child;
	}
	//insert the node of z
	z->parent = y;
	if (NULL == y)
		*root = z;//tree was empty
	else
	{
		if (z->key<y->key)
			y->left_child = z;
		else
			y->right_child = z;
	}
}
void Transplant(PNode *root, PNode u, PNode v)
{
	if (NULL == u->parent)
		*root = v;
	else
	{
		if (u == u->parent->left_child)
			u->parent->left_child = v;
		else
			u->parent->right_child = v;
	}
	if (NULL != v)
		v->parent = u->parent;
}
/*delete a node in the binary search tree*/
void Delete_Tree(PNode *root, int key) //<删除节点
{
	//Find the node you want to delete
	PNode p = Search_Tree(*root, key);
	if (NULL == p->left_child)
		Transplant(root, p, p->right_child);
	else
	{
		if (NULL == p->right_child)
			Transplant(root, p, p->left_child);
		else
		{
			PNode y = Successor_Tree(*root);
			if (y->parent != p)
			{
				Transplant(root, y, y->right_child);
				y->right_child = p->right_child;
				y->right_child->parent = y;
			}
			Transplant(root, p, y);
			y->left_child = p->left_child;
			y->left_child->parent = y;
		}
	}
}
/*print the key of binary search tree*/
void ioder_Tree(PNode root)
{
	if (NULL != root)
	{
		ioder_Tree(root->left_child);
		printf("  %d", root->key);
		ioder_Tree(root->right_child);
	}
}
int main()
{
	int i;
	int Arr[LENGTH] = { 16, 6, 20, 2, 7, 19, 22, 1, 4, 11, 8 };
	PNode root = NULL;
	PNode p = NULL;
	for (i = 0; i<LENGTH; i++)
	{
		Insert_Tree(&root, Arr[i]);
	}
	ioder_Tree(root);
	printf("\n");
	//printf("Hello world!\n");  
	Delete_Tree(&root, 11);
	ioder_Tree(root);
	printf("\n");
	p = Maxmum_Tree(root);
	printf("The Maxmum of node is:%d\n", p->key);
	p = Minimum_Tree(root);
	printf("The Minimum of node is:%d\n", p->key);
	getchar();
	return 0;
}

　　

#include <iostream>
#include <cstdio>
#include <map>
#include <string>
using namespace std;
int main()
{
	///声明（int为键 ， const char* 为值）
	map <int, const char*> m;
	///插入元素
	m.insert(make_pair(1, "ONE"));
	m.insert(make_pair(10, "TEN"));
	m[100] = "HUNDRED";///其他写法
	///查找元素
	map<int, const char*>::iterator ite;
	ite = m.find(1);
	puts(ite->second);
	ite = m.find(2);
	if (ite == m.end())
		puts("no found");
	else
		puts(ite->second);

	puts(m[10]);///其他写法
	///删除元素
	m.erase(10);
	for (ite = m.begin(); ite != m.end(); ++ite)
	{
		printf("%d: %s\n", ite->first, ite->second);
	}
	system("pause");
	return 0;
}