POI2013
Price List
可以发现答案只有三种:要么最短路乘\(a\),要么最短路换成\(b\),要么最短偶数路换成\(b\)。
这里的最短偶数路还要满足不经过\((x,y),(y,z)\)且\((x,z)\)有边。
前两种是平凡的,第三种考虑每次扩展两条边,这样是\(O(m^2)\)的。
不经过的是三元环,只有\(O(m\sqrt m)\)。考虑\((y,z)\)的边如果被经过了就没有必要再经过一次了所以可以删除,只有三元环的边会被重复遍历,时间复杂度\(O(m\sqrt m+n)\)
Triumphal arch
显然先二分变成判定性问题,然后对于某个\(k\)判断可行。
首先肯定要把\(1\)周围围满,然后直接考虑剩下的放哪里似乎有些棘手。
不妨从下往上考虑。设\(f_i\)表示子树内还有多少是需要放的,作为一个点\(x\),肯定要把子树内尽量放满,因为哪边没放满往那边走就输了,因此\(f_u=\sum\limits_{(u,v)\in E}{f_v+1}\)。然后\(f_u=\max(0,f_u-k)\),最后看\(f_1\)是否为\(0\)即可。
时间复杂度\(O(n\log n)\)
Tower Defense Game
首先请您回忆一下您最开始是怎么乱搞最小点覆盖的。
大概是随机一个点的顺序然后看每个点被覆盖了没有,如果没被覆盖了那么就覆盖。
然后这就是这道题做法。因为距离为\(2\),所以无论放一条边哪个端点上都至少有原来距离为\(1\)的效果。
Polarization
什么玩意不同写法空间相差怎么这么大。
首先肯定是选定一个点,然后将它的子树一部分内向,一部分外向。
可以证明选重心最优,然后相当于要考虑一堆数选出一些和最接近一半。
直接bitset\(O(\frac{n^2}{w})\)不太能过,因为物品总和为\(n\),所以只有\(O(\sqrt n)\)种物品,然后二进制拆分成\(O(\sqrt n\log n)\)个之后再bitset就可以做到\(O(\frac{n\sqrt n\log n}{w})\)了。
Walk
牛逼结论好评,卡空间卡时间差评。
首先原题给了一个结论,如果将一个超长方体分成两份,那么两份之间的边数不少于较小的一边的大小。
不知道怎么证明,但是想想很对。
然后可以推导出一个结论:如果这个超长方体被挖去\(n\)个块,那么最多分出一个大于\(nk\)的联通块,因为如果有两个,那么之间的边至少为\(nk+1\)条。
那么爆搜即可,如果所在联通块大小都大于\(nk\)那么就可以直接判定在一个联通块中。
然而并过不去,要手写哈希表。
Laser
马勒戈壁看错题力!
首先按极角排序离散,然后变成有\(n\)个区间,选\(k\)个点使得每个区间最多碰到一个,且碰到的区间数量尽可能多。
设\(dp_{i,j}\)表示到了第\(i\)个区间,选了\(j\)点,预处理\(left_i\)表示经过\(i\)点的区间中最左端是哪个,随便转移。
时间复杂度\(O(nk)\)
Maze
细节真nm多。
首先有解的必要条件是L比P多四个,我们猜这个东西是充要的。
按照多出来的四个L分成四段,每段内L的个数和P的个数相同,正好对应四个象限。
以第一象限为例,我们令起点在\((INF,0)\)处,终点在纵坐标为\(INF\),则可以与下一个象限的起点对应。四个象限可以看作第一象限旋转得到。
L与P相同可以对应到括号上去,因此我们只需要合并两个括号串,和在某个括号串外面加一层。
如果我们令括号串的头尾始终是竖直的,合并两个括号串是平凡的。
在外围加上一对LP的过程大概是这样,打个旋转标记就好了。PL同理。
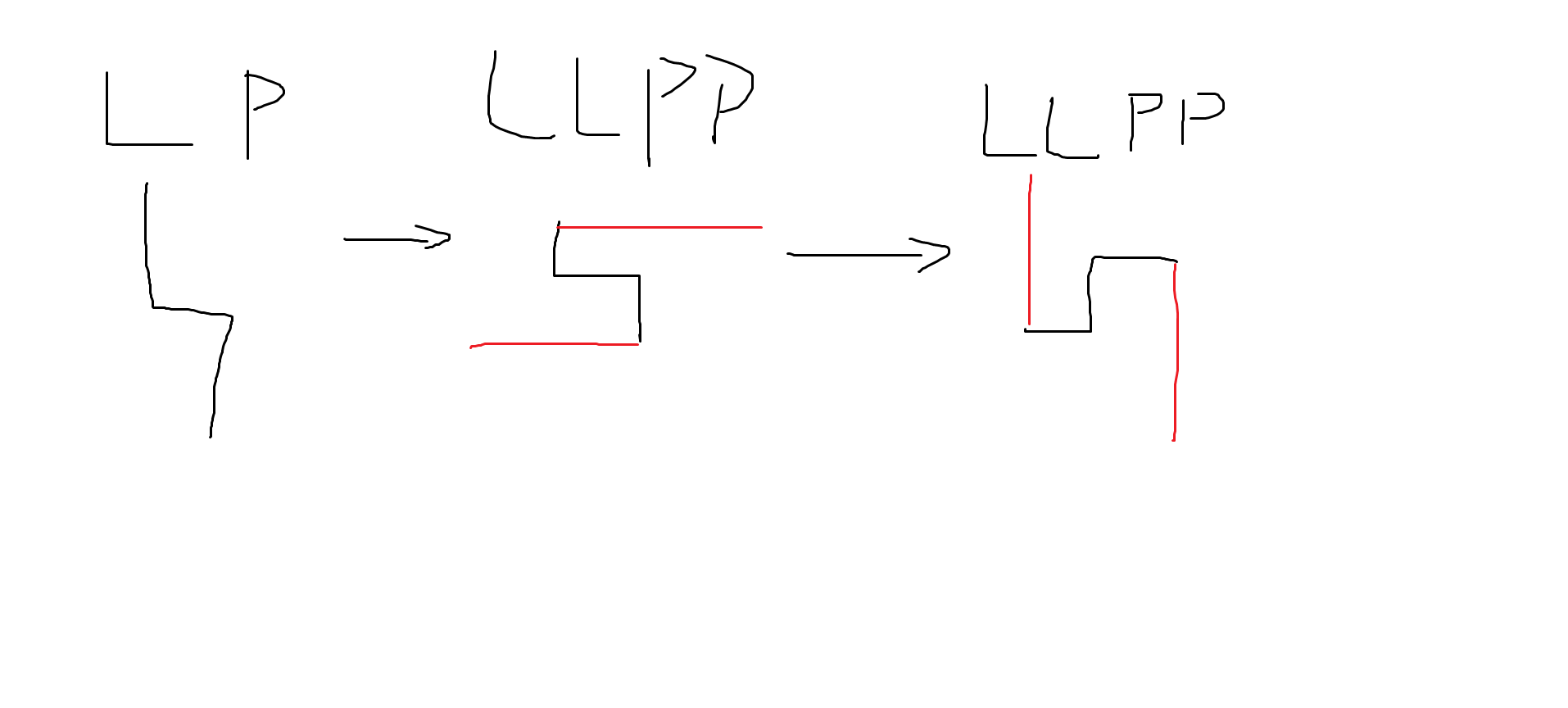
时间复杂度\(O(n)\),注意细节。
Multidrink
貌似直接构造不是很难,为什么题解写了一车东西?
首先我们先来考虑从一个点父亲出发,走过这个点的子树,然后回到这个点的构造,记为\(G_1(x,fa)\)。
同时记从一个点出发,走过这个点的子树,回到这个点父亲的构造为\(G_2(x,fa)\)。两者类似,这里以\(G_1\)的构造为例。
可以发现如果\(x\)的儿子非叶子大于一个是无解的,如果只有一个,记为\(son_x\),那么父亲先一步走到这个点的叶子,然后叶子跳完之后跳到\(son_x\),变成\(G_2(son_x,x)\)。
然后考虑将原图的构造变成一条\(1\)到\(n\)的链,然后加上一些子树。最后要求\(n\)在最后走到。
我们面临一个问题,就是一个点到底是选择以这个点为起点走入,然后构造这个点非链上的子树,还是选择先构造这个点的子树,然后再走到这个点为终点结束构造。
发现最后要求终点为\(n\),我们猜想第二种情况更优,下面的构造过程会说明原因。
记\(F_1(x)\)表示以\(x\)走入,构造完子树走出。记\(F_2(x)\)表示构造完子树后以\(x\)走出,记\(x\)在链上的后继为\(to_x\)。
先考虑\(F_1(x)\),如果\(x\)没有任何子树,那么可以走到\(F_2(to_x)\),也可以走到\(F_1(to_x)\),如果有子树,那么先走非叶子\(G_1(son_x,x)\),再走叶子,然后走到\(F_1(to_x)\)。
再考虑\(F_2(x)\),如果\(x\)没有子树,那么同上,如果有一棵非叶子,那么先走叶子,然后走\(G_2(son_x,x)\)。
特别的,在这种情况下,有两个非叶子是被允许的,分别记为\(son_{x,1}\)和\(son_{x,2}\),先走\(G_2(son_{x,1},x)\),然后走到\(x\),最后走到\(G_1(son_{x,2},x)\),然后变成\(F_1(to_x)\)。
可以看到,在上述的过程中,对\(F_2(x)\)是有要求的,但对\(F_1(x)\)是没有要求的,因此优先走\(F_2(x)\)是更优的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号