关于pushup与pushdown的几种常见情况
适用于线段树、平衡树等树形结构。
注意:
本文中的:
- \(lc(i) = (i \ll 1)\),即 \(i \times 2\)。
- \(rc(i) = (i \ll 1 \mid 1)\),即 \(i \times 2 + 1\)。
一.区间修改,区间求和(求最值)(\(pushdown\))
分两种情况。
1. 将 \([l,r]\) 区间内的每一个数全部赋值为一个数 \(d\)。
此时采用打懒标记(\(lazy\hspace{0.4em}tag\))的方法去解决。把包含在区间 \([l,r]\) 内的节点打上懒标记(即赋值为 \(d\)),每当要访问它的左右儿子时就下传。
想想怎么下传。
令此节点打上的懒标记为 \(x\)。
将左右儿子的值以及懒标记改为 \(x\),再将其懒标记清空。
\(why\ ?\) 很简单。因为整个区间都要赋值为 \(d\),所以左右儿子的子孙也得更改,因此也要打上懒标记。
另外,总和或最值会如何改变?
- \(sum = (r - l + 1) * d\),因为区间内所有数都变成了 \(d\)。
- \(maxn = minn = d\),同上。
代码如下:
inline void pushdown(int id, int tl, int tr){
if (tree[id].tag != -1) { // -1 代表没有懒标记
tree[lc(id)].val = tree[lc(id)].tag = tree[id].tag;
tree[rc(id)].val = tree[rc(id)].tag = tree[id].tag;
tree[lc(id)].minn = tree[lc(id)].maxn = tree[id].tag;
tree[rc(id)].minn = tree[rc(id)].maxn = tree[id].tag;
int tmid = (tl + tr) >> 1;
tree[lc(id)].sum = tree[id].tag * (tmid - tl + 1); // [tl, tmid]
tree[rc(id)].sum = tree[id].tag * (tr - tmid); // [tmid + 1, tr]
rt->tag = -1;
}
}
2. 将 \([l,r]\) 区间内的每一个数全部加上一个数 \(d\)。
同理,也运用懒标记。把包含在区间 \([l,r]\) 内的节点打上懒标记,即加上 \(d\)(因为可能同一区间添加多次)。
类似于第一种。
仍令此节点打上的懒标记为 \(x\)。
将左右儿子的值以及懒标记加上 \(x\),再将其懒标记清空。
另外,总和或最值会如何改变?
- \(sum += (r - l + 1) * d\),因为区间内所有数都加上了 \(d\)。
- \(maxn += d; minn += d\),同上,\(minn\) 与 \(maxn\) 也是如此。
code:
inline void pushdown(int id, int tl, int tr){
if (tree[id].tag != 0) { // 不用 -1 是因为可能区间加上 -1
tree[lc(id)].val += (tree[lc(id)].tag = tree[id].tag);
tree[rc(id)].val += (tree[rc(id)].tag = tree[id].tag);
tree[lc(id)].minn += tree[id].tag; tree[lc(id)].maxn += tree[id].tag;
tree[rc(id)].minn += tree[id].tag; tree[rc(id)].maxn += tree[id].tag;
int tmid = (tl + tr) >> 1;
tree[lc(id)].sum += tree[id].tag * (tmid - tl + 1); // [tl, tmid]
tree[rc(id)].sum += tree[id].tag * (tr - tmid); // [tmid + 1, tr]
rt->tag = 0;
}
}
3. 以上两种操作都有怎么办?
这时就要考虑优先性了。
在加上一个数时,无论之前是否赋值,都不会动摇它的决心。
但在赋值时,之前的添加操作就作废了。
并且,在 \(pushdown\) 中先作赋值操作,再执行添加操作即可。
附上整体代码吧(代码是求 \(maxn\),\(sum\) 可以照葫芦画瓢):
struct Segment_Tree {
struct node { ll maxn, tag1, tag2 = -1; } tree[N << 2];
inline void pushup(int id) {
tree[id].maxn = max(tree[lc(id)].maxn, tree[rc(id)].maxn);
}
// tag1 : add && tag2 : update
inline void pushdown(int id) {
if (tree[id].tag2 != -1) {
tree[lc(id)].maxn = tree[id].tag2;
tree[rc(id)].maxn = tree[id].tag2;
tree[lc(id)].tag2 = tree[id].tag2;
tree[rc(id)].tag2 = tree[id].tag2;
tree[lc(id)].tag1 = 0;
tree[rc(id)].tag1 = 0;
tree[id].tag2 = -1;
}
if (tree[id].tag1) {
tree[lc(id)].maxn += tree[id].tag1;
tree[rc(id)].maxn += tree[id].tag1;
tree[lc(id)].tag1 += tree[id].tag1;
tree[rc(id)].tag1 += tree[id].tag1;
tree[id].tag1 = 0;
}
}
inline void build(int id, int tl, int tr) {
if (tl == tr) {
tree[id].maxn = val[tl];
return ;
}
int tmid = (tl + tr) >> 1;
build(lc(id), tl, tmid);
build(rc(id), tmid + 1, tr);
pushup(id);
}
inline void add(int id, int tl, int tr, int l, int r, int d) {
if (tl > r || tr < l) return ;
if (l <= tl && tr <= r) {
tree[id].maxn += d;
tree[id].tag1 += d;
return ;
}
int tmid = (tl + tr) >> 1; pushdown(id);
add(lc(id), tl, tmid, l, r, d);
add(rc(id), tmid + 1, tr, l, r, d);
pushup(id);
}
inline void update(int id, int tl, int tr, int l, int d) {
if (tl > l || tr < l) return ;
if (tl == tr) {
tree[id].tag1 = 0;
tree[id].maxn = d;
tree[id].tag2 = d;
return ;
}
int tmid = (tl + tr) >> 1; pushdown(id);
update(lc(id), tl, tmid, l, d);
update(rc(id), tmid + 1, tr, l, d);
pushup(id);
}
inline void update(int id, int tl, int tr, int l, int r, int d) {
if (tl > r || tr < l) return ;
if (l <= tl && tr <= r) {
tree[id].tag1 = 0;
tree[id].maxn = d;
tree[id].tag2 = d;
return ;
}
int tmid = (tl + tr) >> 1; pushdown(id);
update(lc(id), tl, tmid, l, r, d);
update(rc(id), tmid + 1, tr, l, r, d);
pushup(id);
}
inline int query(int id, int tl, int tr, int l, int r) {
if (tl > r || tr < l ) return -inf;
if (l <= tl && tr <= r) return tree[id].maxn;
int tmid = (tl + tr) >> 1; pushdown(id);
int lmax = query(lc(id), tl, tmid, l, r);
int rmax = query(rc(id), tmid + 1, tr, l, r);
return max(lmax, rmax);
}
} S;
练手题(\(luogu \hspace{0.1em}P3372\))
二.最大连续子序列 (\(pushup\))
这里有一种类似于 \(DP\) 的方法。
对于一个节点 \(Rt\),我们需要维护四个值。
- \(sum\) : 此区间的总和。
- \(lmx\) : 此区间从左边开头的最大连续子序列。
- \(rmx\) : 此区间从右边开头的最大连续子序列。
- \(mx\) : 此区间的最大连续子序列。
想想怎么从两个儿子更改父亲节点的值。
如下图。

备注:① 代表 \(Rt\) 左儿子的 \(lmx\),② 代表 \(Rt\) 左儿子的 \(rmx\),⑤ 代表 \(Rt\) 左儿子的 \(sum\)。③、④、⑥ 同理。
1. \(Rt\) 的 \(sum\)。
很简单,左右儿子 \(sum\) 的和加上此节点的值即可。
code :
rt->sum = rt->ch[0]->sum + rt->ch[1]->sum + rt->val;
2. \(Rt\) 的 \(lmx\) 。
首先,合并左右儿子的区间后,\(Rt\) 的 \(lmx\) 可以为左儿子的 \(lmx\),即 ① 这一段。
其次,\(Rt\) 的 \(lmx\) 也可以由左儿子的总和、此节点的值与右儿子的 \(lmx\) 的和,即 ⑤ 与 ③ 这两段的和。
两者取最大即可。
code :
rt->lmx = max(rt->ch[0]->lmx, rt->ch[0]->sum + rt->ch[1]->lmx + rt->val);
3. \(Rt\) 的 \(rmx\) 。
与 \(lmx\) 类似的。
首先,\(Rt\) 的 \(rmx\) 可以为左儿子的 \(rmx\),即 ④ 这一段。
其次,\(Rt\) 的 \(rmx\) 也可以由右儿子的总和、此节点的值与左儿子的 \(rmx\) 的和,即 ⑥ 与 ② 这两段的和。
同样取较大者。
code :
rt->rmx = max(rt->ch[1]->rmx, rt->ch[1]->sum + rt->ch[0]->rmx + rt->val);
4. \(Rt\) 的 \(mx\)
最后,\(Rt\) 的 \(mx\) 有三种取值。
- \(Rt\) 左儿子的 \(mx\)。
- \(Rt\) 右儿子的 \(mx\)。
- \(Rt\) 左儿子的 \(rmx\)、此节点的值与右儿子的 \(lmx\) 之和,即 ② + ③。
code :
rt->mx = max({rt->ch[0]->mx, rt->ch[1]->mx, rt->ch[0]->rmx + rt->ch[1]->lmx + rt->val});
最后代码如下:
Code :
inline void pushup(node* &rt) {
if (rt == NIL) return ;
rt->siz = rt->ch[0]->siz + rt->ch[1]->siz + 1;
rt->sum = rt->ch[0]->sum + rt->ch[1]->sum + rt->val;
rt->lmx = max(rt->ch[0]->lmx, rt->ch[0]->sum + rt->ch[1]->lmx + rt->val);
rt->rmx = max(rt->ch[1]->rmx, rt->ch[1]->sum + rt->ch[0]->rmx + rt->val);
rt->mx = max({rt->ch[0]->mx, rt->ch[1]->mx, rt->ch[0]->rmx + rt->ch[1]->lmx + rt->val});
}
三.最小绝对值 (\(pushup\))
即求出所有值中最接近的两个值的绝对值。
如,在序列 \({1,5,9,11,20,25}\) 中,最小绝对值为 \(11-9=2\)。
在二叉搜索树上,左子树的最大值小于等于当前节点值,而右子树的最小值一定大于当前节点值。
由此,一个简单的方法发芽了。
观察下图:
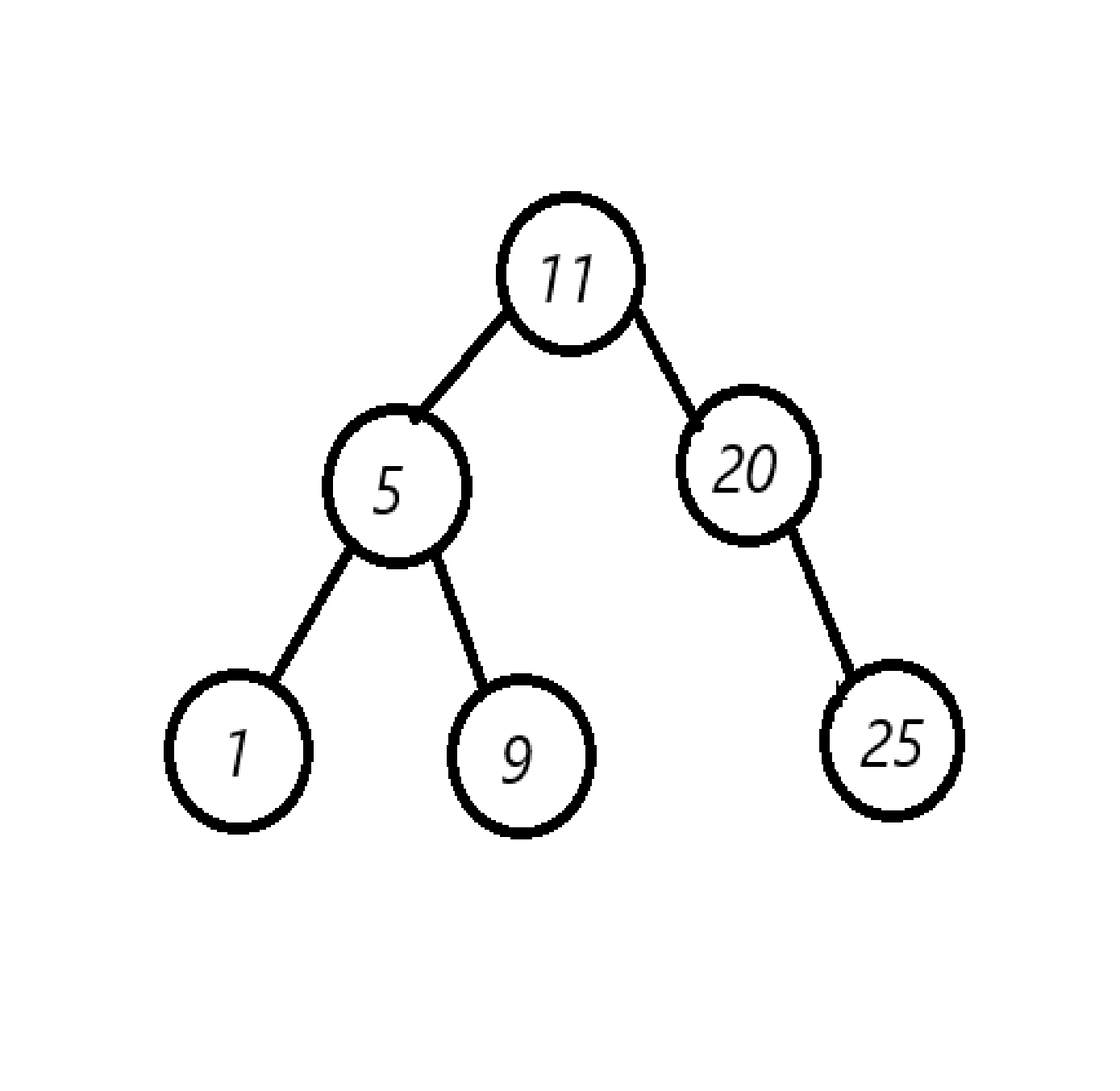
对于节点 \(11\),它左子树的最大值为 \(9\),右子树的最小值为 \(25\),那么,它的最小绝对值为 \(11-9=2\)。
也就是说,每个节点的最小绝对值有以下几种来源:
- 左子树的最小绝对值;
- 右子树的最小绝对值;
- 当前节点值减去左子树的最大值;
- 右子树的最小值减去当前节点值。
这样就能成功维护了。
Code :
inline void pushup(node* &rt) {
if (rt == NIL) return ;
rt->siz = rt->ch[0]->siz + rt->ch[1]->siz + 1;
rt->minn = min({rt->ch[0]->minn, rt->ch[1]->minn, rt->val});
rt->maxn = max({rt->ch[0]->maxn, rt->ch[1]->maxn, rt->val});
rt->mind = min(rt->ch[0]->mind, rt->ch[1]->mind);
if (rt -> ch[0] -> maxn != -inf) rt->mind = min(rt->mind, rt->val - rt->ch[0]->maxn);
if (rt -> ch[1] -> minn != inf) rt->mind = min(rt->mind, rt->ch[1]->minn - rt->val);
}
更新 \(ing...\)
有错误请指出,谢谢!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号