（详解）【线性基 | 异或空间线性基】

前言

本文同步发表于 lg 专栏，链接点这。

---

吐槽：oi-wiki 上写的啥东西啊太高深了看不懂一点。因此本文只有两处参考 oi-wiki。

线性基一般分【异或空间线性基】还有【实数空间线性基】。

对于【异或空间线性基】，有两种构造方法，分别是贪心法和高斯消元法。

Part 0. 异或空间中线性基的定义是什么？

我们讲得简单一点，具体一些线性代数的定义详见 oi-wiki。

假设有一个长 \(n\) 的数组 \(a\)，我们希望构造出一组含有 \(m\) 个元素的线性基 \(p\)，我们令 \(a\) 所有数的组合（不一定要两个数，可以是多个数或 \(1\) 个数）进行异或得到的值的并集为 \(S\)，\(p\) 中所有数的组合进行异或得到的值得并集为 \(T\)，并且删除 \(S\)，\(T\) 中的 \(0\)（即讨论情况为正整数），则满足：

比如 \(a = [1,2,4]\)，则 \(S = \{1\}\cup \{2\}\cup \{4\}\cup \{1\oplus 2\}\cup \{1\oplus 4\}\cup \{2\oplus 4\} \cup \{1\oplus 2\oplus 4\} = \{1 ,2 ,3 ,4,5 ,6 ,7\}\)。

• \(S = T\)。

• \(m\) 在满足条件下最小。

• 注意：\(p\) 中的元素不一定要在 \(a\) 中出现。

有的资料中 \(S\) 是所有数的集合（记作 \(S1\)）而不是组合过后异或值的集合（记作 \(S2\)），其实这两者是等价的。

• 假设 \(T = S1\)，然而 \(S2\) 可以由多个 \(S1\) 中的元素异或产生，而这些元素都可以被 \(T\) 的子集表示，更何况一个数异或两次等于没异或，因此看着每个数可能要挑选大于 \(1\) 次，不符合子集定义，但实际只用挑选 \(0\) 或 \(1\) 次即可满足。

• 也就是说，在 \(S1\) 下生成的线性基 \(p\) 在 \(S2\) 下仍然适用。

• 所以是等价的。

我们最理想得到的线性基，满足 \(p\) 中所有数在二进制下画到矩阵上，每一行第一个 \(1\)（下面简称最高位）所在列上有且仅有它一个 \(1\)。

可能有点难懂，举个例子，比如说 \(p = [1 ,4 ,5]\)，对应矩阵如下，括号里表示列数，实际写矩阵有关代码（比如下文的高斯消元法）肯定是从左到右为 \([1,m]\)（\(m\) 为矩阵列数），这里为了对应二进制位的位数定义才这样，实际矩阵应该也没有这种写法：

\[\begin{bmatrix}(2&1&0)\\0&0&1\\1&0&0\\1&0&1\end{bmatrix} \]

第二行和第三行的最高位都是第 \(2\) 列，不符合我们的设定。

然而，如果 \(p = [1,4,11]\)，可以构造如下矩阵：

\[\begin{bmatrix}(3&2&1&0)\\0&0&0&1\\0&1&0&0\\1&0&1&1\end{bmatrix} \]

尽管第 \(0\) 列中，第 \(1\)，\(3\) 行出现了两个 \(1\)，但是第 \(3\) 行第 \(0\) 列的 \(1\) 不是第 \(3\) 行最高位，所以这是我们想要的线性基。

Part 1. 线性基的几个主要性质和结论

• 参考文献：【学习笔记】浅谈异或线性基。

1. 对于两数 \(a\)，\(b\)，如果 \(a = b\)，那么可以只保留 \(a\)，\(b\) 中的一个。

• 设存在一个数 \(c\)，我们可以删除 \(b\)，因为 \(a = b\)，所以 \(a\oplus c = b\oplus c\)。

• 尽管 \(a\oplus b = 0\)（\(a = b\)），我们讨论范围为正整数，所以我们可以删除 \(b\)。

2. 对于不同两数 \(a\)，\(b\)，我们可以构造出线性基 \(p = [a ,a\oplus b]\)。

• \(S = \{a ,b ,a\oplus b\}\)，\(T = \{a ,a\oplus b ,a\oplus a\oplus b\} = \{a ,a\oplus b,b\}\)（异或具有抵消的性质，即 \(a\oplus a = 0\)），所以 \(S = T\)，且可以证明长度最小为 \(2\)。

3. 线性基中不存在一个子集，使得子集内元素异或值为 \(0\)（很重要的一条性质！）。

• 我们按照编号从小到大插入线性基（不同题目有不同要求）。

• 反证法，设有 \(p_i\)，\(p_j\)，并且准备新插入 \(p\) 的元素为 \(p_k\)（\(i ,j< k \le m\)），若 \(p_i\oplus p_j \oplus p_k = 0\)，即 \(p_i\oplus p_j = p_k\)，则 \(p_k\oplus x = (p_i\oplus p_j)\oplus x\)（其中 \(x\) 为任意的其他子集的异或值），并且 \(p_k\oplus p_i = p_j\)，\(p_k\oplus p_j = p_i\)，发现任意 \(p_k\) 都可以用 \(p_i\oplus p_j\) 替换，或者抵消后（比如上文的 \(p_k\oplus p_i = p_j\)）等价于一个元素，且这个元素属于 \(p\) 的子集，即 \(d_k\) 无用，为了让 \(m\) 尽可能小我们要杀掉它！

• 一句话证明：我们的范围为正整数集。

4. \(a\) 中的任意一个数都可以由 \(p\) 的子集所含值异或得到。

• 严谨的考虑，我们要分类讨论：

• 如果 \(k\) 不能插入线性基，由第 \(3\) 点得一定是因为 \(k\oplus p_i\oplus p_j\oplus \cdots\oplus p_{num} = 0\)，即 \(p_i\oplus p_j\oplus \cdots\oplus p_{num} = k\)，尽管插入不了但还是能表示。

• 如果 \(k\) 能插入线性基，设插入到 \(p\) 中第 \(pos\) 个位置，则 \(k\oplus p_i\oplus p_j\oplus\cdots\oplus p_{num} = p_{pos}\)（\(i <j<\cdots<num<pos\le m\)），即 \(k = p_i\oplus p_j\oplus\cdots\oplus p_{num} \oplus p_{pos}\)，可以被表示。

• PS：第二条这个可能有关线性基代码，先看一下，如何理解下面会写：

inline void insert (int x){
  for (int i = 50 ; i >= 0 ; i --){
    if ((x >> i) & 1) {
      if (!basis[i]) {basis[i] = x ; break;}
      else x ^= basis[i];
    }
  }
}

• 一句话证明：\(S = T\)。

5. 线性基内部的数个数唯一；且在保持性质 \(4.\) 的前提下，数的个数是最少的。

• 这个蒟蒻懒得写了，直接复制、修改了，顺带一点注释：

以下内容除了注释均抄袭摘自【学习笔记】浅谈异或线性基，内容无删除，有小改。

若 \(a\) 里面的所有元素都可以插入到线性基里面，则不管用什么顺序将序列里的数插入线性基，线性基中的元素一定与原序列元素数量相同。

若 \(a\) 里面的一些元素不能插入到线性基里面，则设 \(x\) 不能插入线性基，一定满足形如 \(p_i\oplus p_j\oplus p_k = x\) 的式子。尝试将插入顺序改变为 \(p_i\)，\(p_j\)，\(x\)，\(p_k\)，则 \(p_k\) 就不可能插入成功，原因很简单，留给读者自己思考（注释：因为 \(p_i\oplus p_j\oplus p_k = x\)，得 \(p_i\oplus p_j\oplus x = p_k\)，所以插不进去，原因同 \(3.\)，这样就有 \(0\) 了）。

通俗地说，原来是 \(x\) 插不进去，改变顺序后，则是 \(p_k\) 插不进去。即对于插不进去的元素，改变插入顺序后，要么还是插不进去；要么就是插进去了，同时另一个原来插进去的元素插不进去了。因此，可以插进去的元素数量一定是固定的。

若去掉线性基 \(p\) 里面的任一个数，都会使得 \(a\) 里的数无法通过用线性基里的元素异或得到，没有多余的元素（因为我们在满足 \(S = T\) 的时候 \(m\) 尽可能小)。所以线性基的元素个数在保持 \(3.\) 的前提下，一定是最少的。

6. 对于 \(m > 0\) 个元素的线性基，能够组合异或的非零异或值个数为 \(2^m- 1\)。

• 不可能存在 \(p_k = p_i\oplus p_j\oplus \cdots\oplus p_{num}\)，不然 \(p_k\) 就插不进去。

• 而 \(p_k\) 现在就在线性基里面，所以不满足上式。

• 因此线性基中的任意元素/不属于/其它元素的子集异或和的集合。

• 所以数量即为非空子集数，即 \(2^m - 1\)。

• PS：有的题目可能存在异或值为 \(0\)，而我们线性基不讨论 \(0\)，所以有的题目答案可能为 \(2^m\) 或 \(2^m - 1\)，要注意。

6. 引申：对于一个 \(n\) 个元素，值域为 \(V\) 的序列，线性基的大小最多为 \(log_2{(V+1)}\)。

7. 线性基中元素的子集异或和的集合和原序列的子集异或和的集合相同。

• 显然，我们由性质 \(4.\) 可得 \(a\) 中的所有元素都能被线性基表示，那么 \(a\) 的子集的异或和也可以表示成由多个线性基的元素异或。

• 如果有重复的数异或，由于相同的数异或偶数次抵消，我们把它们看作异或 \(\text{cnt_x}\bmod 2\) 次就可以了，其中 \(cnt_x\) 为数 \(x\) 进行异或出现的次数。

8. 由 \(n\) 个数组成的数组的线性基大小为 \(m\)，则其原数组组合异或能产生 \(2^m\) 个异或值，每个元素出现 \(2^{n - m}\) 次。

• 前半句显然，\(6.\) 证过。

• 后半句我们先由 \(7.\) 得：线性基中元素的子集异或和的集合和原序列的子集异或和的集合相同。

• 于是我们把数组放到线性基上思考。

• 我们相当于再线性基后面补上 \(n - m\) 个 \(0\)，这样每种异或值可以选择异或或者不异或这些 \(0\)，方案数就是 \(2^{n - m}\) 啦。

Part 2. 线性基的构造

啰嗦了这么多，以下就分两种方法：

贪心法

我们记 \(basis_i\) 表示线性基中二进制下第 \(i\) 位（从右往左数，从 \(0\) 开始）的基（数）为多少，也就是说这个数是被插入到了线性基里。

我们要尽可能满足我们理想的线性基，由于要求最高位所在列单独，我们从后往前取二进制位（如 \(1011_{(2)}\) 先从后取 \(1,0,1,1\) 而不是 \(1,1,0,1\)），这样我们线性基插入也是从后往前。

也就是说，这里每一行的数值是从小到大的，第一行的数值 \(<\) 第二行的数值 \(<\) 第三行的数值，以此类推。

并且我们钦定了 \(basis_i\) 的最高位位置为 \(i - 1\)（因为我行从 \(1\) 开始计数，如果从 \(0\) 开始这里就是 \(i\) 了）。

当我们要插入时，当且仅当第 \(i\) 位为 \(1\)，不然不可能做最高位，也不会插入线性基。

当我们发现能插入的时候，分两种情况：

• \(basis_i = 0\)，直接插啊，注意可能会继续插入，比如 \(x\) 经过某种魔法操作后，后面还有多余的 \(1\)，要 break，插好了你就完事了啊。

• \(basis_i \neq 0\)，没办法，只能往后插。

  • 但是这样我们发现会存在多个最高位为 \(1\) 的情况，分别为插入的 \(x\) 和已经存在的 \(basis_i\)。

  • 为了保持线性基的理想，所以我们要让 \(x\gets x\oplus basis_i\)，这样第 \(i\) 位的 \(1\) 就抵消了，这样不影响，因为性质 \(2.\)：

  • 对于不同两数 \(a\)，\(b\)，我们可以构造出线性基 \(p = [a ,a\oplus b]\)（可以推广到多个数）。

  • 相同两数异或一下为 \(0\)，这样死也插不进去，不是正好嘛？

这样确保了这种方法的正确性。

于是打出如下代码：

inline void insert (int x){
  for (int i = 50 ; i >= 0 ; i --){
    if ((x >> i) & 1) {
      if (!basis[i]) {basis[i] = x ; break;}
      else x ^= basis[i];
    }
  }
}

效果展示

当 \(a = [1,5,9,4]\)，从上往下分别是线性基第 \(0\)，\(1\)，\(2\)，\(3\) 位，插入效果：

\[a = [0001_{(2)},0101_{(2)},1001_{(2)},0100_{(2)}] \]

\[\begin{bmatrix}(3&2&1&0)\\0&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}\Rightarrow\begin{bmatrix}(3&2&1&0)\\0&0&0&1\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}\Rightarrow\begin{bmatrix}(3&2&1&0)\\0&0&0&1\\0&0&0&0\\0&1&0&1\\0&0&0&0\end{bmatrix}\Rightarrow\begin{bmatrix}(3&2&1&0)\\0&0&0&1\\0&0&0&0\\0&1&0&1\\1&0&0&1\end{bmatrix}\Rightarrow{\boxed{1}}\begin{bmatrix}(3&2&1&0)\\0&0&0&1\\0&0&0&0\\0&1&0&1\\1&0&0&1\end{bmatrix}\Rightarrow p = [1 ,5 ,9] \]

\(\boxed{1}\)：此时插入 \(4\)，\(4\) 的第 \(2\) 位与 \(5\) 的第 \(2\) 位重复，因此 \(4\oplus 5 = 1\)，然后又与 \(1\) 的第 \(0\) 位重复，\(1\oplus 1 = 0\)，插不进去了。

注：上面重复默认为含 \(1\) 位，下同。

而当我们插入顺序为：

\[a = [1 ,9 ,4 ,5] \]

\[\begin{bmatrix}(3&2&1&0)\\0&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}\Rightarrow\begin{bmatrix}(3&2&1&0)\\0&0&0&1\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}\Rightarrow\begin{bmatrix}(3&2&1&0)\\0&0&0&1\\0&0&0&0\\0&0&0&0\\1&0&0&1\end{bmatrix}\Rightarrow\begin{bmatrix}(3&2&1&0)\\0&0&0&1\\0&0&0&0\\0&1&0&0\\1&0&0&1\end{bmatrix}\Rightarrow{\boxed{2}}\begin{bmatrix}(3&2&1&0)\\0&0&0&1\\0&0&0&0\\0&1&0&1\\1&0&0&1\end{bmatrix}\Rightarrow p = [1 ,4,9] \]

\(\boxed{2}\)：此时插入 \(5\)，\(5\) 的第 \(2\) 位与 \(4\) 的第 \(2\) 位重复，因此 \(4\oplus 5 = 1\)，然后又与 \(1\) 的第 \(0\) 位重复，\(1\oplus 1 = 0\)，插不进去了。

贪心法的特点

综上，我们可以发现如下特点：

• \(basis_i < basis_j\)（\(i < j\) 且 \(basis_i ,basis_j \neq 0\)）。

• \(basis_i\) 的最高位位置为 \(i\)（\(basis_i \neq 0\)）。

• 线性基的构造不唯一，贪心法构造的线性基中的元素与数据大小无关，与插入顺序有关，越靠前的数越先尝试被插入。

  • 所以有的题目要按照某种方式先排序再贪心求线性基。

• 它不一定是构造出我们理想的线性基。

这个显然，若数 \(x\) 插入了 \(basis_i\)，则 \(basis_j\)（\(i < j\)）的第 \(i\) 位可能也是 \(1\)，但它并不是最高位。

比如董晓老师视频中，只要你时间划到 \(2:00\)，右边就有两个例子：

当 \(a = [5 ,6 ,9 ,10]\) 时，\(p = [3 ,5 ,9]\)，矩阵：\(\begin{bmatrix}(3&2&1&0)\\0&0&0&0\\0&0&1&1\\0&1&0&1\\1&0&0&1\end{bmatrix}\)。

但是仅仅换一下位置，\(a = [6 ,5 ,9 ,10]\) 时，\(p = [3 ,6 ,9]\)，矩阵：\(\begin{bmatrix}(3&2&1&0)\\0&0&0&0\\0&0&1&1\\0&1&1&0\\1&0&0&1\end{bmatrix}\)。

容易发现，第二个矩阵中 \(0011_{(2)}\) 的最高位所在列有 \(6\) 的第一位，并非我们理想的线性基。

分享这个例子还有一个原因，就是它也阐述了线性基的元素与插入顺序有关。

这个时间复杂度为 \(\mathcal O(n\log V)\)，\(V\) 为值域，效率挺高。

例题

P4570 [BJWC 2011] 元素。

简述题意：有 \(n\) 个物品，属性为 \(a\)，\(b\)，要求选出一些物品，使得它们的属性 \(a\) 构成的集合不存在任何子集使得异或值为 \(0\)，并且 \(b\) 属性之和最大，求这个最大的 \(b\) 属性之和。\(1\le n\le 10^3\)，\(1\le a\le 10^{18}\)，\(1\le b\le 10^4\)。

敏锐地注意到到：

属性 \(a\) 构成的集合不存在任何子集使得异或值为 \(0\)。

于是我们通过某条性质想到线性基。

发现这就是线性基板子，但是好像又不能直接线性基，这样不能使 \(b\) 属性之和最大。

但是我们想到线性基内元素与插入顺序有关，且越靠前的元素越先尝试被插入线性基，于是想到先按照 \(b\) 从大到小排序，然后套板子，最后累加和就做完了。

const int N = 1e3 + 10;
int n ,basis[70];
int ans;
struct node {int num ,magic;}a[N];

inline bool insert (int x){
//insert 返回 1，表示 x 成功被插入线性基；返回 0，则表示不能插入线性基。
  dn (i ,63 ,0) {
    if ((x >> i) & 1) {
      if (!basis[i]) {
        basis[i] = x;
        return 1; 
      } x ^= basis[i];
    }
  } return 0;
} inline bool cmp (node x ,node y) {return x.magic > y.magic;}//按照属性 b 排序，题目中为魔法值 magic。

signed main (){
  n = read ();
  up (i ,1 ,n) a[i].num = read () ,a[i].magic = read ();
  sort (a + 1 ,a + 1 + n ,cmp);
  up (i ,1 ,n) 
    if (insert (a[i].num)) ans += a[i].magic;
  writeln (ans);
  return 0;
}

如何提升？

我们想要构造理想的线性基，就要让它改进！但是我们又无从下手。

当然，这就引出了我们另一种构造方法，它的构造方法是我们真正理想的线性基，这个就叫做：

高斯消元法

• 参考文献：@Weslie 的 题解：P3812 【模板】线性基Weslie。

同样的，我们先把每个数写进矩阵：

\[a = [1,5,9,4] \]

\[\begin{bmatrix}(1&2&3&4)\\0&0&0&1\\0&1&0&1\\1&0&0&1\\0&1&0&0\end{bmatrix} \]

假设我们想要第 \(i\) 行的最高位 \(1\) 是在从左上到右下的这条对角线上，这样从第一行到最后一行的 \(1\) 一定从后往前（按照列的编号），也就是说 第一行数值 \(>\) 第二行数值 \(>\) 第三行数值，以此类推。

也就是说，我们要第一行第一列存在一个 \(1\)，但是目前没有！

于是我们把第三行和第一行交换一下，这样第一行通过交换做了主元，就可以达到我们的目的啦：

\[\begin{bmatrix}(1&2&3&4)\\1&0&0&1\\0&1&0&1\\0&0&0&1\\0&1&0&0\end{bmatrix} \]

然后我们来到第二行第二列，但是我们发现已经有 \(1\) 了，可以光明正大做主元，于是不交换。

可是第四行还有一个 \(1\)，我们要把它消掉！

于是我们让第四行的元素整体异或上对应列的元素，这样还是可以构造线性基，原因是某个性质，留给读者自己思考。

变成这样：

\[\begin{bmatrix}(1&2&3&4)\\1&0&0&1\\\color{red}{0}&\color{blue}{1}&\color{green}{0}&\color{purple}{1}\\0&0&0&1\\\color{red}{0}&\color{blue}{1}&\color{green}{0}&\color{purple}{0}\end{bmatrix} \Rightarrow\begin{bmatrix}(3&2&1&0)\\1&0&0&1\\\color{red}{0}&\color{blue}{1}&\color{green}{0}&\color{purple}{1}\\0&0&0&1\\\color{red}{0}&\color{blue}{0}&\color{green}{0}&\color{purple}{1}\end{bmatrix} \]

来到第三行第三列，我们发现这是 \(0\)，并且同列没有 \(1\)，于是跳过；

来到第四行第四列，我们发现不用换，但是第四列居然都是 \(1\)？怎么办？只消一个？那不行。那咋办？当然是全部消掉啦！

变成这样：

\[\begin{bmatrix}(3&2&1&0)\\1&0&0&1\\0&1&0&1\\0&0&0&1\\0&0&0&1\end{bmatrix}\Rightarrow \begin{bmatrix}(3&2&1&0)\\1&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&1\end{bmatrix} \]

然后我们就得到了线性基 \(p = [8 ,4 ,1]\)。

inline void insert (){
  int k = 1;//k 为需要作主元的行。11
  dn (i ,50 ,0) {//相当于从 1~logV（大概）枚举列。 
    up (j ,k ,n)
      if ((a[j] >> i) & 1) {
        swap (a[j] ,a[k]);//找到替身，交换，第 i 行做主元（狡猾/doge）。
        break;//找到了就别换了省时间。
      }
    if (!((a[k] >> i) & 1)) continue;//留给读者思考。
    up (j ,1 ,n)
      if (j ^ k && ((a[j] >> i) & 1)) a[j] ^= a[k]; // 1.同行不异或 ； 2.该列有 1 才异或，以消除该列的所有 1，不然可能会违反某些线性基的性质，这里留给读者思考；3.注意是 [1,n] 不是 [k+1,n]，可以看上面举得例子。
    ++ k;
    if (k == n + 1) break;//做完了 1~n 行，该干的都干完了，break。
  } 
}

总结一下高斯消元法的特点：

• 一定能够构成我们理想的线性基，即每一行的最高位都是 \(1\)。

• 最后的矩阵是一个‌行最简形矩阵，这点通过过程很好理解。

行最简矩形：主元必须为 \(1\) 且主元所在列的其他数都为 \(0\) 的矩阵。

高斯消元法的时间复杂度为 \(\mathcal O(n\log V)\)，和贪心法求线性基效率相当。

例题

P3857 [TJOI2008] 彩灯。

简述题意：有 \(n\) 个灯泡和 \(m\) 个开关构成，再给定一个 \(m\) 行 \(n\) 列的数组 \(a\)，若第 \(i\) 行第 \(j\) 列的值为 O，那么按下开关 \(i\) 可以改变灯泡 \(j\) 的状态；若为 X，则不能。一开始所有灯都是关闭状态。你可以按下若干次所有按钮，求最终展现出来的所有灯的不同状态的数量，全关也算一种状态。

一个开关改变状态，相当于异或操作。

然后我们把按一个开关看作异或这个开关对应的数值，数值由开关的影响灯泡决定，比如开关 \(x\)：OXXOO，那么我们异或上 \(1\times 2^0 +0\times 2^1+0\times 2^2+1\times 2^3+0\times 2^4 = 25\)。

这样题意就转化成了：已知 \(m\) 个数的序列 \(a\)，求它们组合异或后（或一个数）可以产生多少种不同的异或值。

还记得这条性质嘛

6.对于 \(m\)（\(m > 0\)） 个元素的线性基，能够组合异或的非 \(0\)异或值个数为 \(2^m- 1\)。

因此我们只要求出线性基大小，答案即为 \(2^{\text{线性基大小}} - 1 + 1 = 2^{\text{线性基大小}}\)，注意还有 \(0\) 的情况，因此加 \(1\)。

这样高斯消元法和贪心法都可以做。

注意取模，还有如果求 \(2^x\) 懒得写快速幂或者直接乘，应该写 1ll << x 而非 1 << x。

---

等等，写了这么点，我们难道只是构造线性基玩嘛？不可能，它一定有它的作用。

Part 3. 线性基用途

1.【本题】求线性基组合异或最大值

本题等价于这个问题，至于为什么线性基的组合异或最大值，等于原序列的组合异或最大值（或者更多下述操作），上面已经提到了，可以请读者思考一下。

贪心法

直接搞贪心。

直接上代码：

inline int qmax (){
  int res = 0;
  dn (i ,50 ,0) if ((res ^ basis[i]) > res) res ^= basis[i];
  return res;
}

为什么这样贪心是正确的？

前置知识：\(1\underbrace{(0/1)(0/1)\cdots(0/1)}_{x 个二进制位} > 0\underbrace{111\cdots1}_{x 个 1}\)（\(x>0\)），证明很简单，知道的跳过，不知道的可以转化为十进制思考。

由于前置知识的缘故，对于异或 \(basis_i\)，我们只关心最高位会不会影响答案的大小。

• \(basis_i = 0\)：值不变。

• \(basis_i \neq 0\)：则这一行有主元，最高位一定为 \(1\)（定义）。

  • \(res\) 这一位为 \(0\)，一定异或，原因如前置知识；

  • \(res\) 这一位为 \(1\)，\(1\oplus 1 = 0\)，不取，后面的异或值最高位权值更小，所以不能异或，不然 \(res\) 肯定变小。

这样确保了贪心的正确性。

高斯消元法

直接异或就行了，因为每一个高位所在列最多一个 \(1\)，我们关注高位可以舍掉更低的位，这样也是正确的。

inline int qmax (){
  int res = 0;
  dn (i ,50 ,0) res ^= a[i];//up (i ,0 ,50) 也可以。
  return res;
}

PS：时间复杂度指总体时间复杂度。

2.求线性基组合异或最小值

答案为线性基中最小的元素，因为最高位的 \(1\) 位置都不同，所以线性基中的数异或任意一个其他数都是比它更大。

但是注意答案可能还为 \(0\)。如果插入线性基的个数不足 \(n\)，那么答案一定存在 \(0\)，可以请读者自己思考，插不进去的情况是什么（性质也有）。

这个代码是我口胡，如果有问题请评论。

贪心法

inline int qmin (){
  int zero = 0;//zero 表示原序列插入线性基的个数（奇怪。
//n：原序列长度。
  for (int i = 0 ; i <= 50 ; i ++) zero += (basis[i] != 0);//basis[i] != 0 表示插入进线性基了。
  if (zero != n) return 0;//basis != n ==> 有的没插进去，答案为 0。
  for (int i = 0 ; i <= 50 ; i ++) if (!basis[i]) return basis[i];//basis[i] < basis[i + 1]（去除 0 的情况）。
} 

这个代码也是我口胡，有问题评论！

高斯消元法

int zero = 0;
for (int i = 1 ; i <= 50 ; i ++)//高斯消元我的代码编号从 1 开始。
  zero += (a[i] != 0) ;
if (zero != n) return 0;//同上。
for (int i = 50 ; i >= 1 ; i --)
  if (a[i]) return a[i];//对于高斯消元法，basis[i] > basis[i + 1]（去除 0 的情况）。

3.求组合异或第 \(k\) 小/大值。

以第 \(k\) 小值为例，第 \(k\) 大值读者可以自己思考，思路差不多。

贪心法

• 当异或值有 \(0\)（可以判断）的时候，让 \(k\gets k - 1\)，然后分类：

• \(k = 0\)，答案为 \(0\)；

• \(k \ne 0\)，我们需要重新构建线性基，让矩阵上每一行的最高位所在列的 \(1\) 个数只有一个，也就是说我们想要线性基满足：\(basis\) 在第 \(i\) 位上只有 \(basis_i\) 为 \(1\)。

• 可以通过异或抵消的方式，对于 \(basis_i\) 的第 \(j\) 位为 \(1\)（\(1\le j< i\)），可以让 \(basis_i\gets basis_i\oplus basis_j\)，这样我们能够保留最高位上的 \(1\)，并且消去最高位同列的其余 \(1\)（可以手动模拟过程助于理解）。

• 但是要按照数值从小到大以方便贪心，而重建后就 \(basis\) 却默认从小到大排序了，这点很容易想到。

• 这样的好处是啥？这样我们可以对 \(k\) 进行二进制分解，如果第 \(i\) 位为 \(1\)，那么答案异或上 \(basis_i\)。执行结束后的答案即为异或组合的第 \(k\) 小值。

• 这样的正确性有保证，因为：

  • 我们选取两个最高位不一样且都为 \(1\) 的数异或，最高位分别为 \(i\)，\(j\)，并记作 \(a_i\oplus a_j\)（\(j<i\)），而所有第 \(j\) 位上多余的 \(1\) 在重建过程中一定会消去，所以异或之后值更大，第 \(i\)，\(j\) 位上一定出现 \(1\)。

  • 但是由【前置知识】得，我们只要再选一个含有更高位的 \(1\) 且不等于 \(a_i\)，就一定能异或出一个更大的值。

  • 多个数同理。

  • 于是二进制分解可行！

• 注意新建一个数组记录 \(basis\)，因为有的 \(basis\) 为 \(0\) 哦！

inline int q_k(int k){
  //处理 zero。
  if (zero != n) -- k ;
  if (!k) return 0;
//----
// rebuild basis.
  for (int i = 0 ; i <= 50 ; i ++)
    for (int j = 0 ; j < i ; j ++)
      if ((basis[i] >> j) & 1)//basis[i] 除了 i 位置为 1，尝试抵消，抵消不成功也没关系，说明前面也没成功，可以错开，后面也可以抵消。
        basis[i] ^= basis[j];//重构线性基。
  int cnt = 0;
  for (int i = 0 ; i <= 50 ; i ++)
    if (basis[i]) p[cnt ++] = basis[i];//注意！
//------
  if (k > (1ll << cnt) - 1) return -1 ; //无解。等价于 k >= (1ll << cnt)。
  for (int i = 50 ; i >= 0 ; i --)
    if ((k >> i) & 1) res ^= p[i];
  return res;
}

‌	‌原始贪心法线性基‌	‌重建后的线性基‌
‌最高位重 \(1\)	可能重叠	完全消除
‌元素顺序‌	有关插入顺序	按值从小到大排序
‌第 \(k\) 小计算‌	大概率不行（不满足最高位 \(1\) 独立）	直接二进制分解

时间复杂度瓶颈在于重建线性基，为 \(\mathcal O(log^2 V)\)。

高斯消元法

更简单了！

还是二进制分解，同样，因为高斯消元的结果是我们理想的线性基，最高位的 \(1\) 都错开了，直接二进制分解就可以了。

需要注意的是，高斯消元求得的线性基是从大到小排列，应当注意（见代码片段）。

inline void insert (){
  k = 1;
  dn (i ,50 ,0) {
    up (j ,k ,n)
      if ((a[j] >> i) & 1) {
        swap (a[j] ,a[k]);
        break;
      }
    if (!((a[k] >> i) & 1)) continue;
    up (j ,1 ,n)
      if (j ^ k && ((a[j] >> i) & 1)) a[j] ^= a[k];
    ++ k;
    if (k == n + 1) break;
  }  
} inline int q_k (int x){
  int res = 0;
  if (k < n + 1) -- x;
  dn (i ,k - 1 ,0) if ((x >> i) & 1) res ^= a[k - i - 1];//因为我们求第 k 小，而 a 是降序排序，我们要去小的，所以是 a[k - i - 1]（试一下就知道了/doge）。
  return res;
} 

\(3.\) 的反操作：求一个在线性基内出现过的元素 \(x\) 在所有异或和内的排名（定义为小于 \(x\) 的数加 \(1\)）。

性质 \(8.\) 是怎么说来着？

由 \(n\) 个数组成的数组的线性基大小为 \(m\)，则其原数组组合异或能产生 \(2^m\) 个异或值，每个元素出现 \(2^{n - m}\) 次。

也就是说，我们只需要求出异或和小于 \(x\) 的个数，答案即为 \(2^{n-m}\times \text{个数} + 1\)。

一种是记录下这 \(2^m\) 个元素，排序后直接查（或者二分)，但是 \(2^m\) 可以被 1 2 4 8 16... 卡成 \(V\)，不可取。

另一种是对 \(x\) 二进制分解，若第 \(i\) 位 \(basis_i \neq 0\) 则令 \(ans\gets ans + 2^{\text{前面 basis 非 0 个数}}\)，至于原因读者可以自己思考。

模板题 | P4869 albus就是要第一个出场。

好了现在说原因：这个选的话后面选与不选都影响最终异或值，我们需要重构线性基才能保证，但是敲了代码又发现其实不用重构线性基（大雾，具体原因可以上网。

那么答案是 \(rk\times 2^{n - m} + 1\)（记作 \(ans\)）。

这里我们似乎算上了 \(x\)，本应该 \(ans\gets ans - 2^{n - m}\)，但是 \(0\) 的情况我们要算上，所以还要特判。

但是这题的特殊性是空集也算 \(0\)，所以 \(ans\gets ans - 2^{n - m} + 2^{n - m} = ans\)（如果我理解有误可以评论）。

# include <bits/stdc++.h>

# define int long long
# define up(i ,x ,y) for (int i = x ; i <= y ; i ++)
# define dn(i ,x ,y) for (int i = x ; i >= y ; i --)

using namespace std;

inline int read (){int s = 0 ; bool w = 0 ; char c = getchar () ; while (!isdigit (c)) {w |= (c == '-') ,c = getchar () ;} while (isdigit (c)){s = (s << 1) + (s << 3) + (c ^ 48) ; c = getchar ();}return w ? -s : s;}
inline void write (int x){if (x < 0) putchar ('-') ,x = -x; if (x > 9) write (x / 10) ; putchar (x % 10 | 48);}
inline void writesp (int x){write (x) ,putchar (' ');}
inline void writeln (int x){write (x) ,putchar ('\n');}

const int N = 1e5 + 10 ,mod = 10086;
int n ,m ,basis[35] ,a[N] ;

inline void insert (int x){
  dn (i ,31 ,0) {
    if ((x >> i) & 1) {
      if (!basis[i]) {
        basis[i] = x;
        ++ m;
        return ;
      } x ^= basis[i];
    }
  }
} int tot ,b[35];
inline int q_rk (int x){
  int rk = 0 ,mul = 1;
  up (i ,1 ,n - m) mul = ((mul * 2) % mod);
  up (i ,0 ,30) if (basis[i]) b[tot ++] = i;//记录一下 basis[i] != 0 的位置。
  up (i ,0 ,tot - 1) if ((x >> b[i]) & 1) rk += (1ll << i) % mod ,rk %= mod;
//                           注意这里是 b[i]。         这里是 i。
//                           原因只要理解了就知道。
  return (rk * mul % mod + 1) % mod;
} signed main (){
  n = read () ;
  up (i ,1 ,n) a[i] = read () ,insert (a[i]);
  int Q = read ();
  writeln (q_rk (Q));
  return 0;
}

---

下面的操作是我看了文章 https://www.luogu.com.cn/article/zo12e4s5 才了解到了。

４.询问存在性：判断数 \(x\) 能不能用线性基中的数异或得到

看看能不能插入线性基，如果可以说明不行，因为不存在线性基的子集使得异或值为 \(x\)；如果能插入，就可以异或得到，因为这样存在线性基的子集使得异或值为 \(x\)。

具体可见开头的某条性质。

代码类似。

线性基合并

这里不是指线性基元素的并集，而是把一个线性基插入到另一个线性基。

设有线性基 \(p\) 和 \(p'\)，只要把 \(p'\) 的元素插入 \(p\) 就可以了，插不进去就算了。

// 令 p' -> q
for (int i = 0 ; i <= 50 ; i ++)//O(log V)
  if (q[i]) insert (q[i]); // insert 内容一样，这里是插入 p 中。 O(log V)

或者有时候我们干脆直接新建一个线性基：

for (int i = 0 ; i <= 50 ;i ++) res[i] = 0;
for (int i = 0 ; i <= 50 ; i ++) if (p[i]) insert (p[i]);
for (int i = 0 ; i <= 50 ; i ++) if (q[i]) insert (q[i]);
//这里的 insert 是插入到新的线性基 res 中。

总时间复杂度：\(\mathcal O(log^2 V)\)。

线性基求交

蒟蒻也不会，只能详见 oi-wiki 了。

Part 4. 例题

线性基结合其他东西才是好（毒瘤、弱智）题嘛。

一、线性基结合博弈论：P4301 CQOI2013 新 NIM 游戏

简述题意：有 \(n\) 堆石子，每堆石子有 \(a_i\) 个石头，第一回合双方可以拿走任意堆数的石子，可以不拿，但不能拿光；第二回合以后每人要么拿走一个石子，要么拿走一堆石子，最后取到最后一根火柴的人赢。A 先拿，B 后拿。问 A 想要获胜，第一轮最少需要拿走几个石子？

第二轮以后的规则是 NIM 游戏，NIM 游戏的必败是石子数量的异或和为 \(0\)。

那么 A 就要把可能异或和为 \(0\) 的数的并集拿走，留给 B 一个子集异或和不可能为 \(0\) 的集合。

由于 B 不能取光，他取走 \(x\) 堆后剩下的堆数子集异或和还是不可能为 \(0\)。

此时转变到 NIM 游戏，先手必胜。

注意到要取的最少，于是我们按照石子数量降序排序（插入线性基的基综合最大），答案就是 \(\text{总数}-\text{线性基的基之和}\)。

因为要排序，所以我们使用贪心法。

signed main (){
  n = read ();
  int _all = 0;
  up (i ,1 ,n) a[i] = read () ,_all += a[i];
  sort (a + 1 ,a + 1 + n ,greater <int> ());
  up (i ,1 ,n) 
    if (insert (a[i])) ans += a[i];
  writeln (_all - ans);
  return 0;
}

二、线性基结合图论 P4151 [WC2011] 最大XOR和路径

参考题解 this & this。

线性基结合图论。

我们可以把图抽象成若干条主链和环。

我们分类讨论如下情况：

1. 一条链。

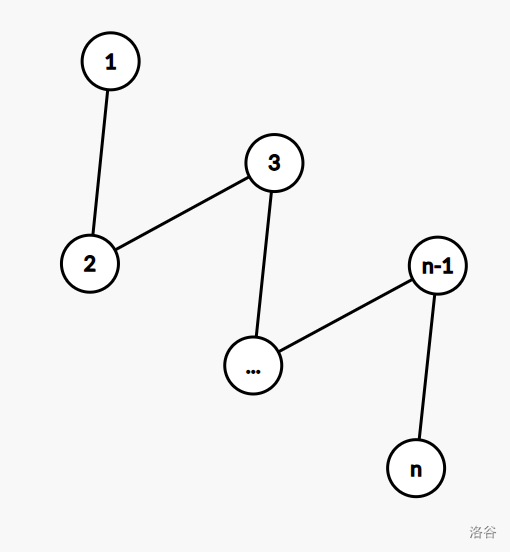
记 \(dis_i\) 为 \(1\) 到 \(i\) 路径上的这条主链的异或和。

答案为 \(dis_n\)。

2. 一条主链 \(+\) 若干个环

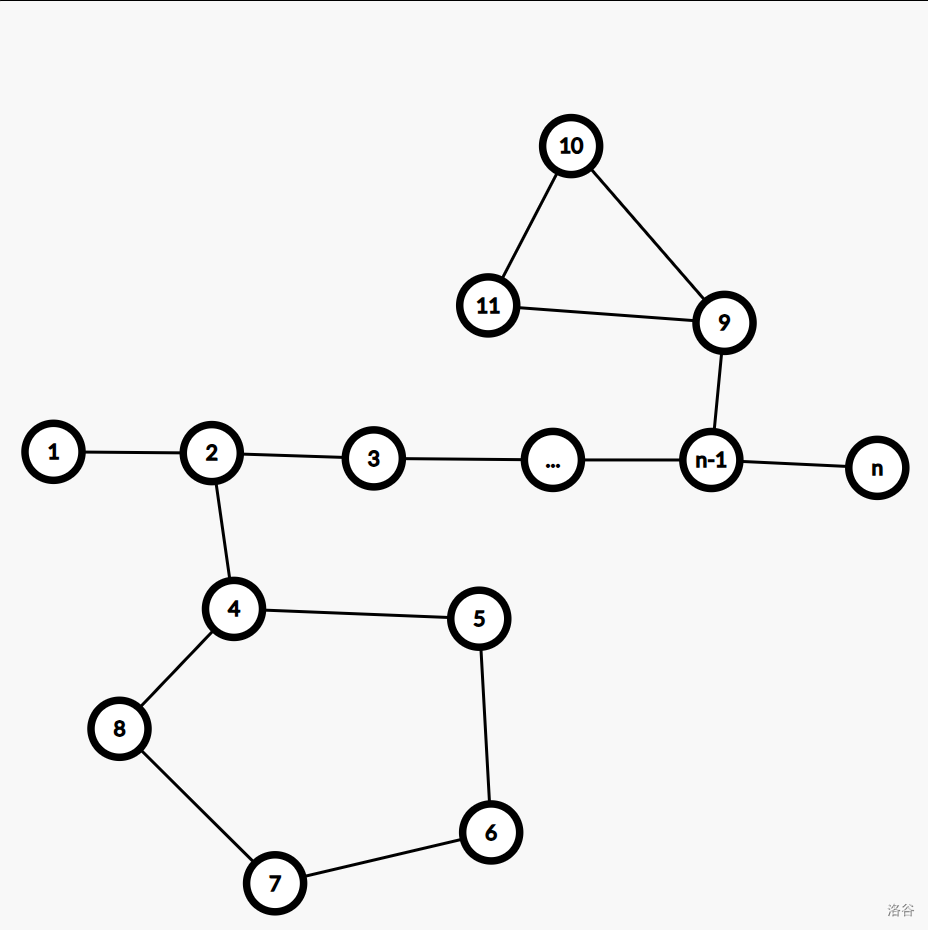
• 不经过环为 \(dis_n\)。

• 经过环（比如环 \(1\)）：\(w_{1,2} \oplus w_{2 ,4} \oplus \text{环 1 异或值} \oplus w_{2 ,4}\oplus w_{2,n} = dis_n\oplus \text{环 1 异或值}\)。

• 也就是说，这种情况下，答案为 \(dis_n \oplus \text{经过的所有环的异或和}\)。

两者取 max 即可，第二种经过哪些环呢？可以构造线性基然后贪心求最大啊。

这种情况：

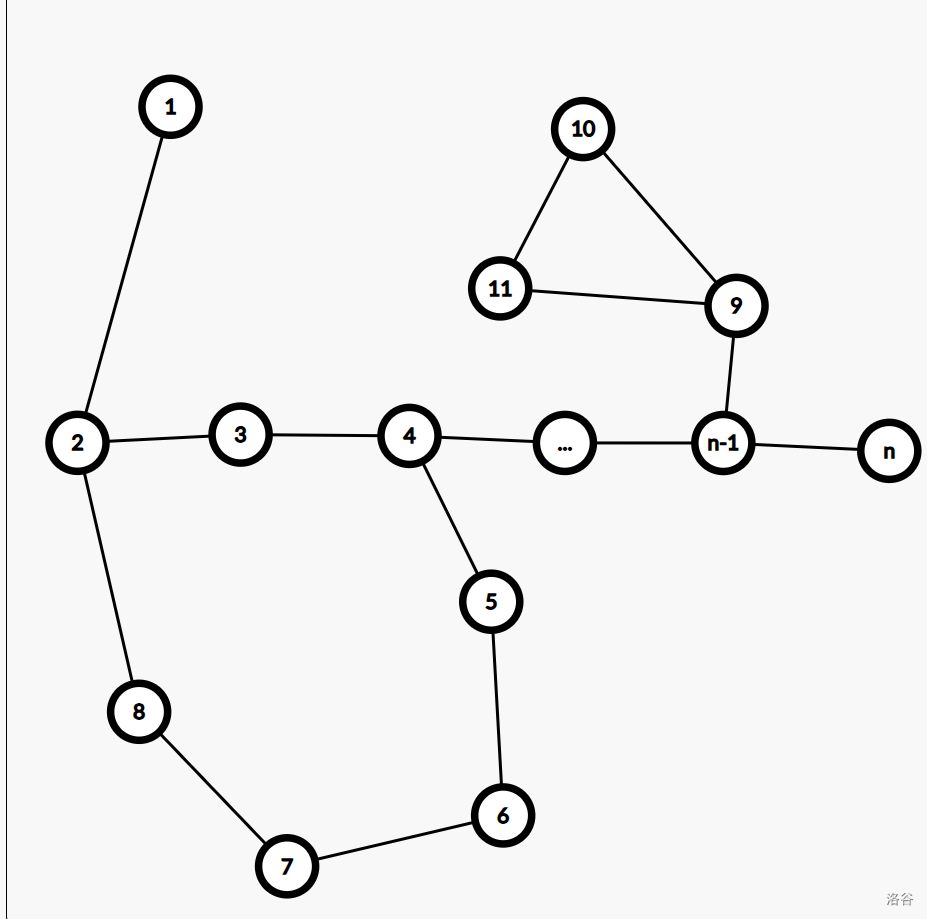
• 直接走主链，答案为 \(dis_n\)；

• 不走主链，那就是绕一半圈走过去，容易得证多绕圈就是上面和这种情况，异或值都抵消了。

针对第二种情况，我们讨论，如果是走半圈，这个异或和貌似不好算。

但是我们还是算上整个异或和，最后异或一下 \(dis_n\)，好像中间的 \(2-3-4\) 就消掉了！这样我们成功实现了走半圈。

这个 \(9-10-11\) 的环处理方式和上面一样。

也就是说我们还是可以把它们丢到线性基里面，答案为 \(\max\{dis_n \oplus \text{经过的所有环的异或和}（这两者异或要最大） ,dis_n\}\)。

3. 多条主链

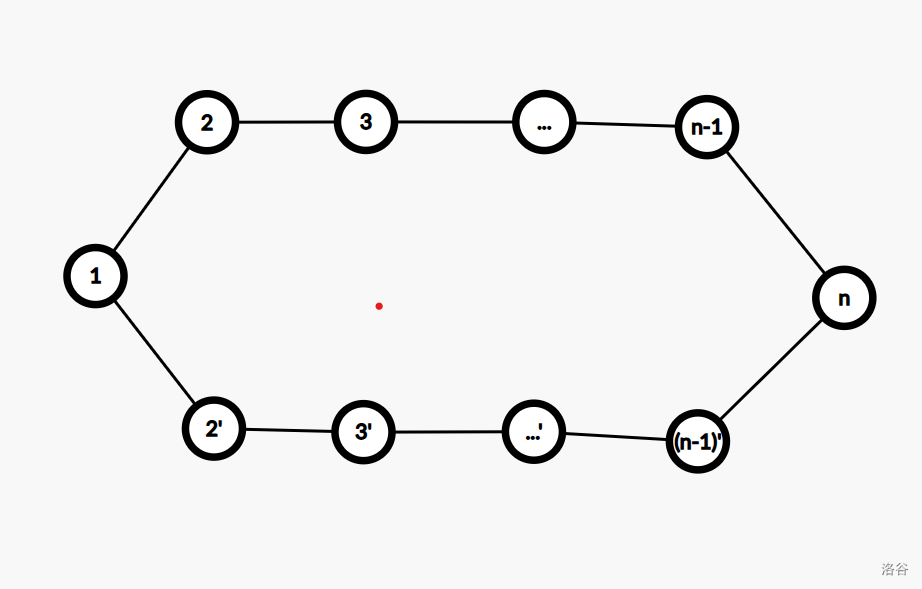
多条主链必将构成环。

设图中的环异或和为 \(x\)。

然后退化了前面的情况。

若上面的链的异或和为 \(dis_n\)（下面的同理）。

• 走上面的链：\(dis_n\)；

• 因为 \(w_{1,2',\cdots,n} = w_{1,2,\cdots,n} \oplus x\)，所以下面的链为 \(dis_n\oplus x\)。

• 所有路径经过异或抵消就是上面两种情况。

多主链同理。

还是可以把环的权值丢尽线性基，做法和上面一样。

容易推广到更多主链，这里读者自己思考吧。

PS：既然多主链都构成环了，那么下文看作一条主路径和环。

4. 环套环

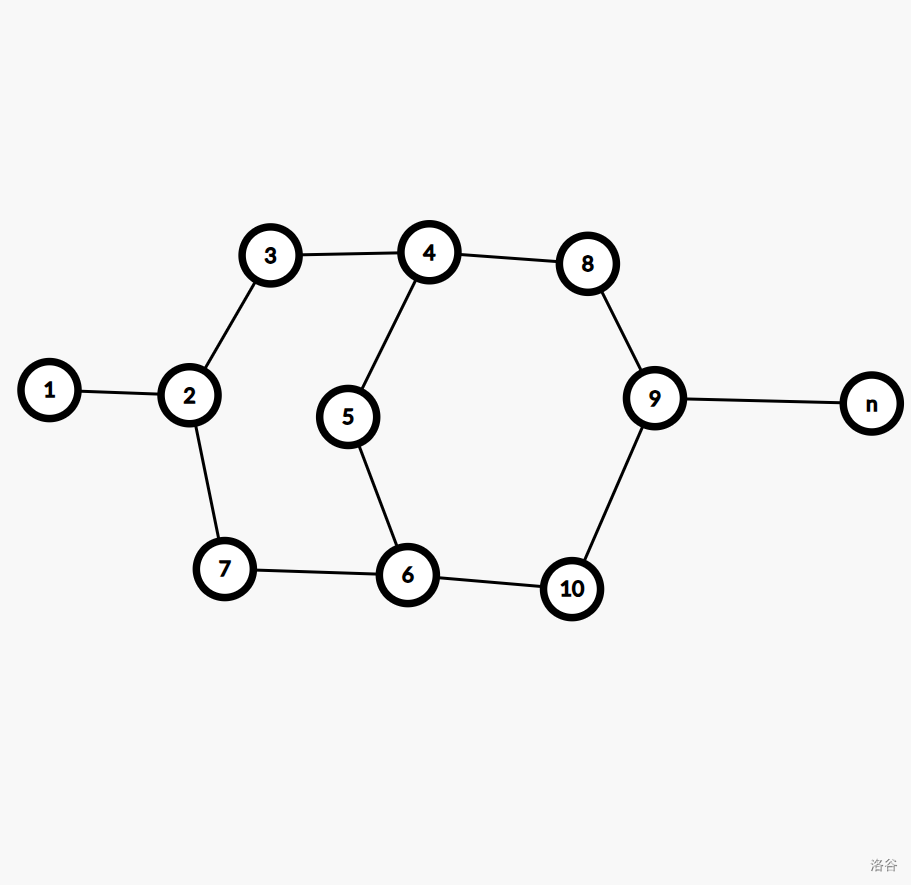
老思路，还是把环丢进线性基就可以了。

正确性可以自己图上画画，这里打字卡顿文章字数过多，我也没把握，就留给读者自己思考。

但是此时环套环会不会漏掉情况呢？

我们把图的一些点抽象一下：

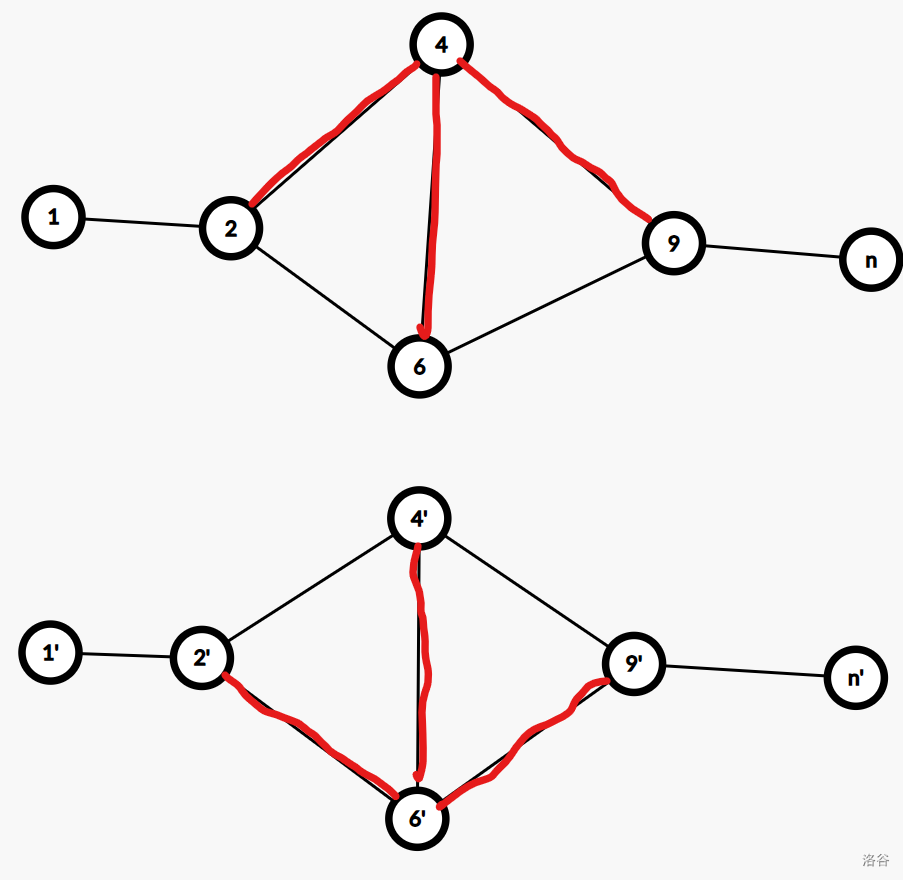
通过模拟的方式，我们从 \(2\) 开始 dfs，能够得到环 \(\{2,4,6\}\) 和 \(\{2,4,6,9\}\)，下图和上图反一下没啥本质区别。

但是我们却漏了 \(\{4,6,9\}\)。

但是我们又惊奇地发现，这两个环异或一下又得到了这个环！\(w_{2,4}\oplus w_{4,6}\oplus w_{2,6} \oplus w_{2,4}\oplus w_{4,9}\oplus w_{6,9}\oplus w_{2,6} = w_{4,6}\oplus w_{4,9}\oplus w_{6,9}\)。

还有一种情况同理，留给读者思考或者看开头的题解链接，图放着了：

---

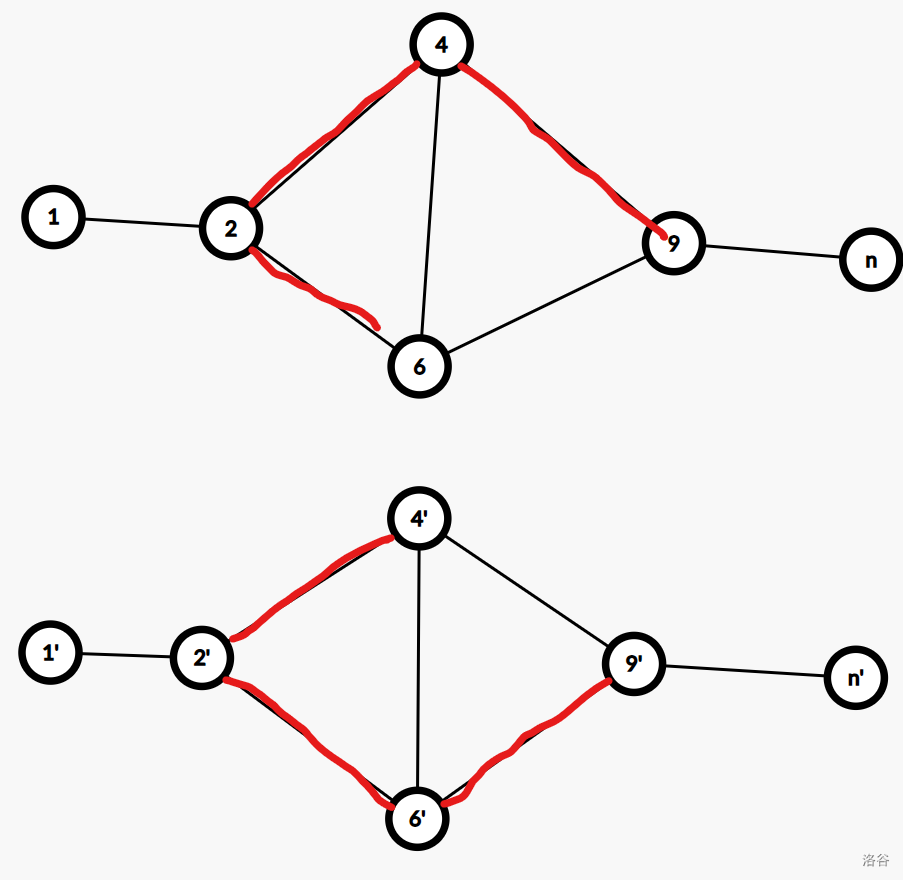
上面这五种情况验证了我们思路的正确性，可以打出代码：

inline void dfs (int u ,int Xor){
  vis[u] = 1 ,dis[u] = Xor;
  for (auto i : edge[u]) {
    int v = i.first ,w = i.second;
    if (vis[v]) insert (Xor ^ w ^ dis[v]); // 计算环的异或值。**
    else dfs (v ,Xor ^ w);
/*
         1  ------ 2 --------------- 3 
                    \                 \
                     \                 \
                      \                 \
                       5-----------------4
此时 u = 5 ,v = 2。
XOR {2-3-4-5-2} = XOR{1-2-3-4-5} ^（异或）XOR {2 - 5} ^ XOR {1 - 2}
                =      dis[u]    ^          w        ^ dis[v]               
*/
  }
}

3.线性基结合数据结构 P4839 P 哥的桶

这里和板子不一样的是，它求的是“区间”异或最大值，而不是全局异或最大值。

更重要的是，它还有单点修改操作！于是我们想到线段树。

我们于是把线性基放到线段树上，空间大小为 \(\mathcal O(4n\log V)\)（省略常数 \(4\) 是 \(\mathcal O(n\log V)\)，严格意义上的空间复杂度是这个不是上面那个，空间足够）。

然后逐步分析操作:

• 1 k x：将价值为 \(x\) 的球插入桶 \(k\)。我们在线段树上寻找一条从根到 \(k\) 的路径，对于路径上的所有节点插入一个 \(x\) 就行了。

• 2 l r：从线段树上找到区间内的节点对应的线性基，开一个新的线性基 \(x\) 合并它们，然后贪心就行了。我们也可以在向上合并的过程中采取线性基合并的方法，但是代码多一点，不用！（当然有的题目这种方法不合适，要用线性基合并）

inline void insert (int* BASIS ,int x){//将 x 插入到线性基 BASIS。
  dn (i ,63 ,0) {
    if ((x >> i) & 1) {
      if (!BASIS[i]) {
        BASIS[i] = x;
        return ;
      } x ^= BASIS[i];
    }
  }
} inline int qmax (){
  int res = 0;
  dn (i ,63 ,0) res = max (res ,res ^ ans[i]);//贪心取最大值。
  return res;
}
inline void ins (int u ,int l ,int r ,int x ,int v){
  insert (basis[u] ,v);//沿路路径一定包含 x，直接插。
//最坏情况插树高次，每次 O(log V)，一次时间复杂度为 O(log nlog V)。 
  if (l == r) return ;
  int mid = ((l + r) >> 1);
  if (x <= mid) ins (u << 1 ,l ,mid ,x ,v);
  else ins (u << 1 | 1 ,mid + 1 ,r ,x ,v);
} inline void query (int u ,int l ,int r ,int ql ,int qr){
  if (l >= ql && r <= qr) {
    up (i ,0 ,31)//O(log V)
      if (basis[u][i]) insert (ans ,basis[u][i]); //把可能的答案插入新建的线性基。 O(log V)。
//学过线段树的都知道，这样一个区间最坏被分为了 log2 (区间长度) 的子区间。
//最坏情况 l = 1 ,r = n，log n 个子区间，一次时间复杂度为 O(log n log^2 V)。
    return ;
  } int mid = ((l + r) >> 1);
  if (ql <= mid) query (u << 1 ,l ,mid ,ql ,qr);
  if (mid < qr) query (u << 1 | 1 ,mid + 1 ,r ,ql ,qr);
}

设操作 \(1\) 有 \(m1\) 次，操作 \(2\) 有 \(m2\) 次，总时间复杂度为 \(\mathcal O(m1\log n\log V + m2\log n\log^2 V)\)，具体原因见代码注释。

Part 5.习题

蒟蒻通过多个资料翻到了这个题单，推荐一下，但是 P3265 [JLOI2015]装备购买是实数空间线性基的模板，与异或空间线性基无关。

Part 6.异或空间线性基的扩展

前缀线性基（时间线线性基）

我们可能想过求全局异或最大值用线性基，有没有想到求区间异或最大值也用线性基呢？

我们上一篇写过可以用线性基 \(+\) 线段树解决，但是时间复杂度却是 \(\mathcal O(m1\log n\log V + m2\log n\log^2 V)\)。

于是我们用了一种时间复杂度为 \(\mathcal O(n\log V)\) 的前缀线性基（注意：不带修改），但是空间复杂度也为 \(\mathcal O(n\log V)\)。

---

采用可持久化线段树的思想，我们新建多个版本，第 \(i\) 个版本代表插入 \(a_{1,2,\cdots,i}\) 的线性基。

我们仍旧记 \(basis_{i ,j}\) 为第 \(i\) 个版本位置为 \(j\) 的基，\(pos_{i ,j}\) 为 \(basis_{i ,j}\) 这个数在 \(a\) 中的位置（下标）（后面有用）。

注意在插入一个元素之前先要复制 \([1,i-1]\) 的线性基，我们是基于它上进行插入。

这个时候的插入仍然分如下情况，插入数 \(x\)，其在 \(a\) 中位置为 \(i\)：

PS：以下的有几个本来应该是 \(basis_{i - 1,j}/pos_{i-1,j}\)，因为版本复制了，又为了和代码一致所以写了 \(basis_{i - 1,j}/pos_{i,j}\)，请读者注意区分。

• \(basis_{i ,j} = 0\)，则直接插入，记录 \(basis_{i ,j} \gets x\)，$pos_{i ,j} \gets i $。

• \(basis_{i ,j} \neq 0\)，我们要做的肯定时 \(x\gets x\oplus basis_{i ,j}\)，但是此时我们还要先做一件事：

  • 当 \(pos_{i ,j} < i\) 时，我们要交换 \(basis_{i ,j}\) 和 \(x\)，以及 \(pos_{i ,j}\) 和 \(i\)。

  • 也就是说，此时我们要用新的 \(x\) 和 \(i\) 去插入线性基。

  • 但是注意，这里要给 \(i\) 找一个替身，不然 \(basis_{\color{red}{i},j}\) 会指向某个我们不想要的东西。

为什么？

• 考虑到我们想要 \([l,r]\) 的区间异或和最大，我们又遵循高位优先原则，在同高位的时候我们一定要让插入顺序尽可能后面，这样更有可能被我们的查询区间所包含，从而增大最大异或和。

• 但这样是否会对低位有影响？我们转念一想，原来线性基能够异或出来的异或和，现在的线性基也能够做到。

• 这样感性理解一下吧，严谨的证明我也不知道。

然后在我们贪心的时候，需要选择 \(pos_{r,i}\ge l\) 的进行贪心，否则不在区间内部。

时间复杂度在插入和询问一次都是 \(\mathcal O(\log V)\)，所以总复杂度为 \(\mathcal O((n + m)\log V)\)，\(n\) 为插入次数，\(m\) 为询问次数。

模板题：CF1100F Ivan and Burgers。

分析：直接套板子。

inline void insert (int i ,int x){
  up (j ,0 ,30) basis[i][j] = basis[i - 1][j] ,pos[i][j] = pos[i - 1][j];//复制前一版本。
  int now = i;
  dn (j ,30 ,0) {
    if ((x >> j) & 1) {
      if (!basis[i][j]) {
        basis[i][j] = x;
        pos[i][j] = now;//对应信息不要搞错。
        return ;
      } if (pos[i][j] < now) swap (x ,basis[i][j]) ,swap (now ,pos[i][j]);//交换。
      x ^= basis[i][j];//如果需要交换则交换后再异或；否则直接异或。
    }
  }
} inline int qmax (int l ,int r){
  int res = 0;
  dn (i ,30 ,0)
    if (pos[r][i] >= l) res = max (res ,res ^ basis[r][i]);//只有在 [l,r] 内才贪心取异或最大值。
  return res;
}

好像还有一种做法是普通线性基 \(+\) 猫树，太巨了蒟蒻不会 stoorz %%%。这边还是推荐好打 \(+\) 好理解 \(+\) 代码短的前缀线性基。

习题 & 前缀线性基的迁移 + 应用题 | P3292 [SCOI2016] 幸运数字。

删除线性基

顾名思义，每个数都有一个插入和删除的时间，每次要询问某个时间内最大的异或和（或线性基有关的问题）。

贪心地，我们想要更高位地基能够在后面的“求组合异或最大值”中发挥更多的作用，我们要它的删除时间尽可能晚！

设这个插入的数为 \(x\)，删除时间为 \(delt\)。

同理分类讨论，设 \(tim_i\) 为第 \(i\) 位的基的删除时间：

• \(basis_i = 0\)：直接插，并记录下数值和删除时间。

• \(basis_i\neq 0\)：分情况：

  • 如果 \(tim_i < delt\)，则让 \(tim_i\gets delt\)（贪心思想），\(basis_i\gets x\)。

  • 反之啥也别做。

• 最后 \(x\gets x\oplus basis_i\)，正确性同上“前缀线性基”。

但是貌似有大佬把它们合并了？！如果是本蒟蒻理解有误请尽快评论 QWQ。

对于求最大异或和，我们还是贪心做，只是这次要求删除时间在要求时间之后就试试能不能增大 \(res\) 而已。

详见代码。

inline void insert (int x ,int delt){
  dn (i ,50 ,0)
    if ((x >> i) & 1) {
      if (tim[i] < delt) swap (tim[i] ,delt) ,swap (basis[i] ,x);
      if (!delt) break;
      x ^= basis[i];
/*
1.basis[i] = 0 。
此时 tim[i] = 0，而 delt > 0，如果不删除我们肯定让 delt 为最晚时间 + 1。
所以执行 tim[i] < delt，两个 swap 恰好达到初始化的效果。
此时 delt = 原tim[i] = 0，break 了，达到了插完完事的目的。
2.basis[i] != 0。
此时这些话还是要执行。
---
综上所述，stoorz %%% 参考 tj 区合并代码的巨佬。
*/
    }
} inline int qmax (int tim){//查询 tim 时刻的最大异或和。
  int res = 0;
  for (int i = 50 ; i >= 0 ;i --)
    if (tim[i] > tim) res = max (res ,res ^ basis[i]);//删除时间比当前时刻晚，说明还存在，可以试试。
  return res;
} 

但是这玩意儿是离线的，我要知道每个点的删除时间才能做，你无法知道删除时间，要看后面信息，处理麻烦（猜测）。

习题：当可删除线性基碰上了图论 | P3733 [HAOI2017] 八纵八横。

The end

到这里，蒟蒻异或空间线性基的内容就结束啦！！！感谢阅读。

总结：异或空间线性基可以用于处理异或问题，通常为多个数异或问题，有的时候会结合其他算法进行出题，大家要灵活辨认，并且灵活运用。

闲话：这百度 AI 写的什么东西啊看不上一点没有达到我想要的效果，还是蒟蒻自己写好了，可能总结很差，不喜勿喷（附上蒟蒻询问百度 AI 的高清美图）。