【小 trick】并查集当链表

有的时候并查集可以当链表使用！

或许你不信，我们举个例子康康：

比如区间覆盖 \([1,2]\)，\([4,8]\)，\([3,7]\)，\([2,6]\) 这四个区间内的正整数，但是已经覆盖过得不用覆盖了。

• 我会暴力！直接循环就行了啊。

  • 但是当 \(1\le \text{值域}\le 10^6\) 时覆盖 \(1000\) 个区间就 T 飞了。

• 我会线段树！把询问离线，然后倒着套板子！

  • 不错的选择，时间复杂度为 \(\mathcal O(\text{覆盖次数}\times \log {值域})\)。

• 我会双向链表！指向右边第一个没有被覆盖的点和左边第一个没有被覆盖的点，右边没有则指向 \(\text{值域}+1\)，左边没有则指向 \(0\)，然后暴力就行了，这样保证了每个点只会访问一次！

  • 很棒！但是修改右边要倒着做，左边要正着做，我们只想要一个循环，更何况这个细节太多了。
  • PS：如果只指右边修改指针时需要整个区间遍历，所以这里使用两个指针。

• 我会并查集！只用维护向右的指针到并查集树上就可以了！

一开始所有点都指向自己：

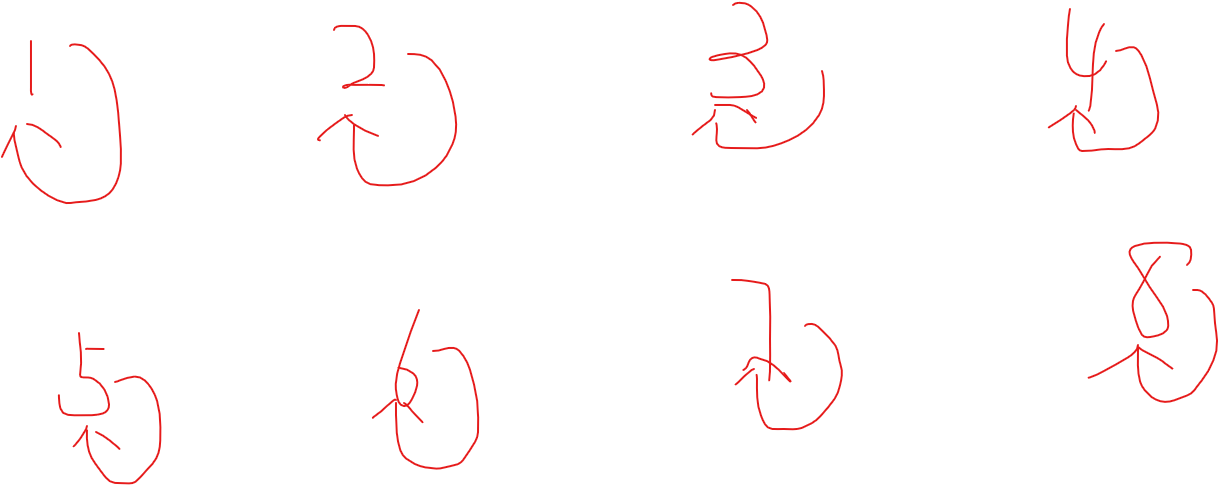
• 我们用 \(find(x)\) 表示 \(x\) 所处并查树上的根，这里也指 \(x\) 下一个未被覆盖的编号（包括自己）。

• 我们从 \(find (l)\)（\(l\) 为区间左端点，\(r\) 为右端点） 开始，记 \(i = find (l)\)，并修改 \(fa_i = i+1\)。

• 下一次跳跃，我们跳跃到 \(find (i + 1)\)，并再记作 \(i\)，重复上述过程。

• 知道 \(i > r\) 为止，结束。

这样看着跳跃很费时间，但是实际上每个点都只会遍历一次，时间复杂度为 \(\mathcal O(\text{值域})\)！

为啥？单纯的并查集 inline int find(int x) { return x == fa[x] ? x : find (fa[x]);} 是不行的，但是我们可以请出我们的常见优化：路径压缩！

这样每个节点到根的距离很短，甚至有的为 \(1\)，很快（并查集常识）。

示例：

第一次覆盖 \([1,2]\)：

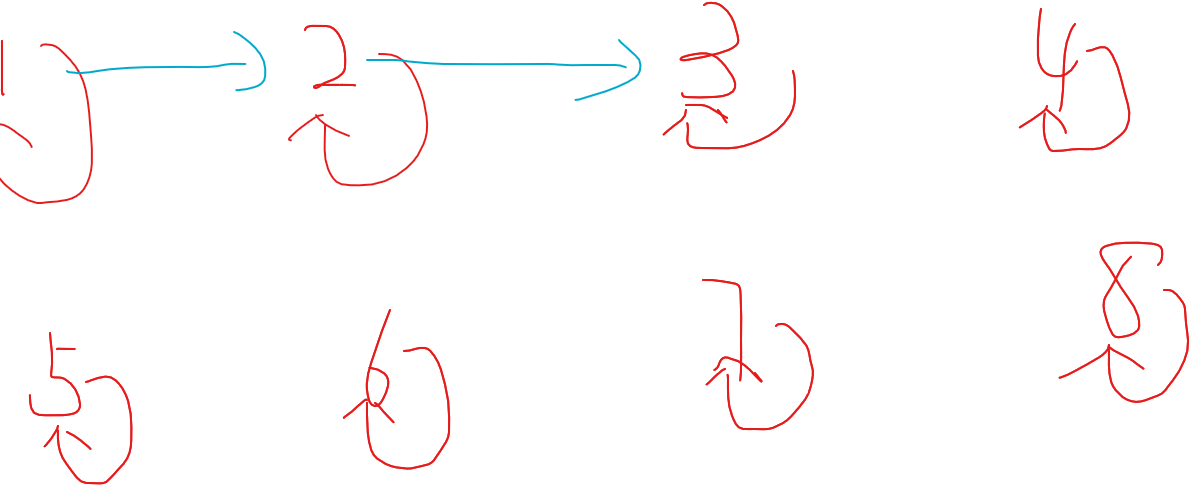
第二次覆盖 \([4,8]\)：

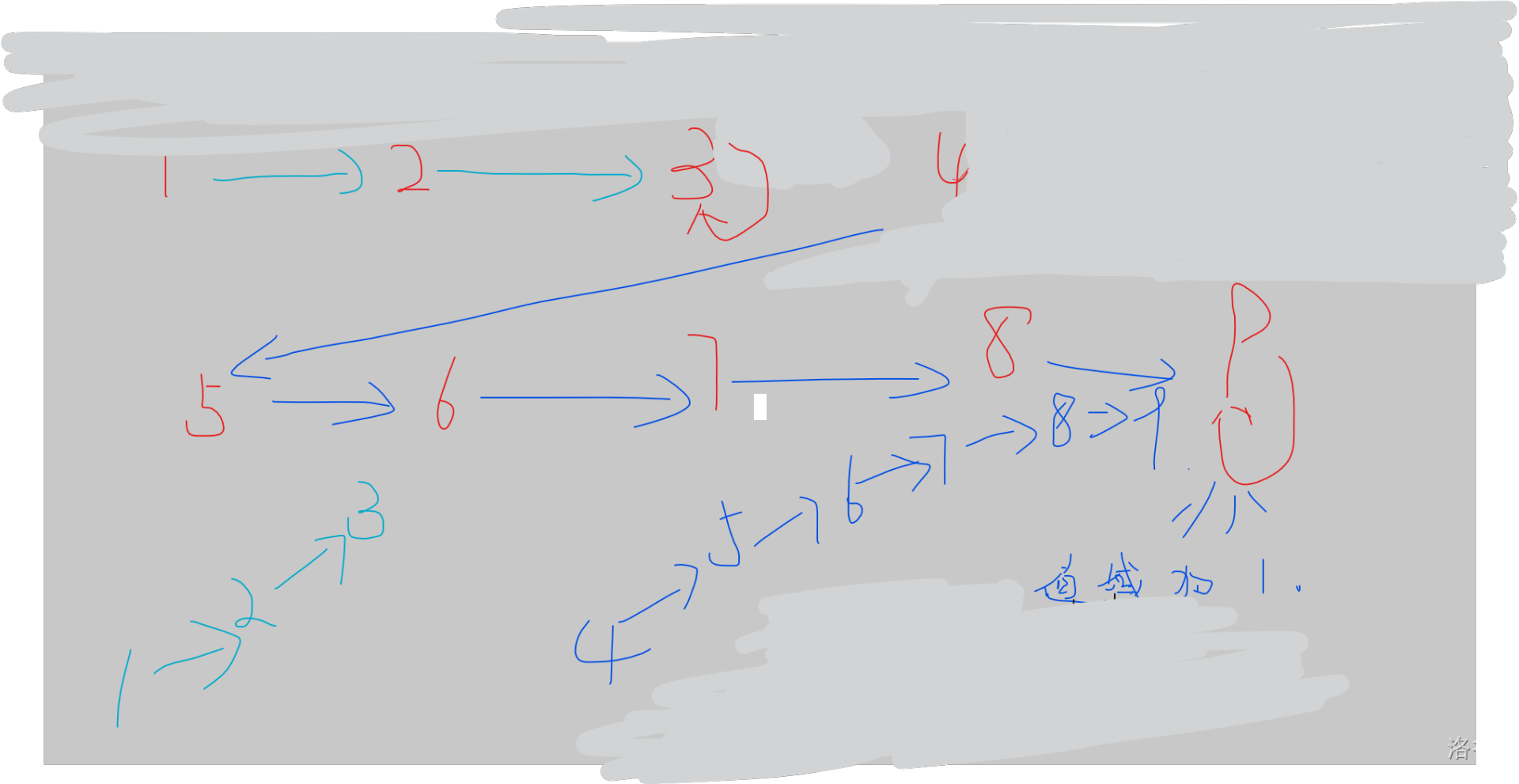
第三次覆盖 \([3,7]\)：

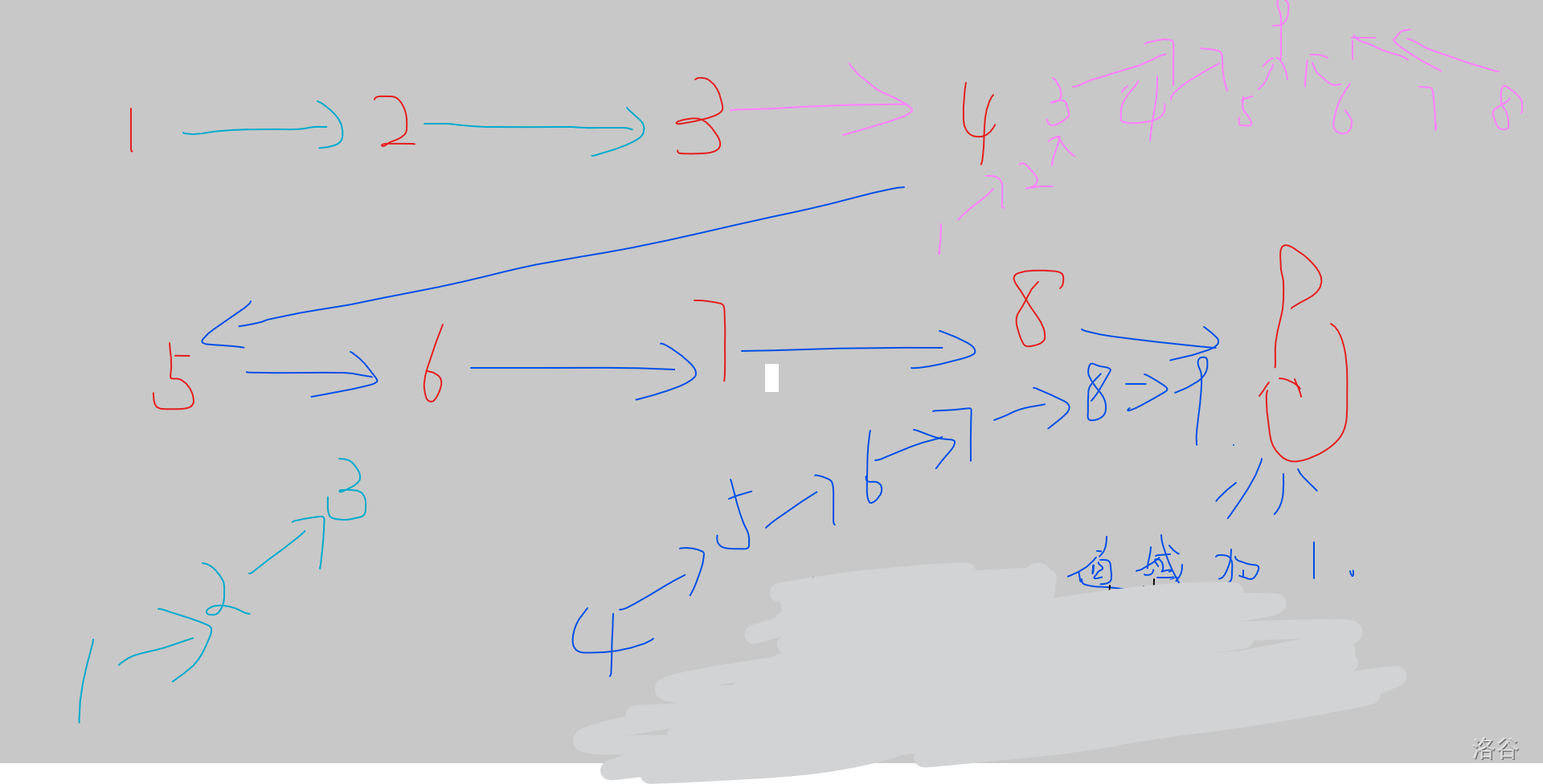
第四次覆盖 \([2,6]\)：

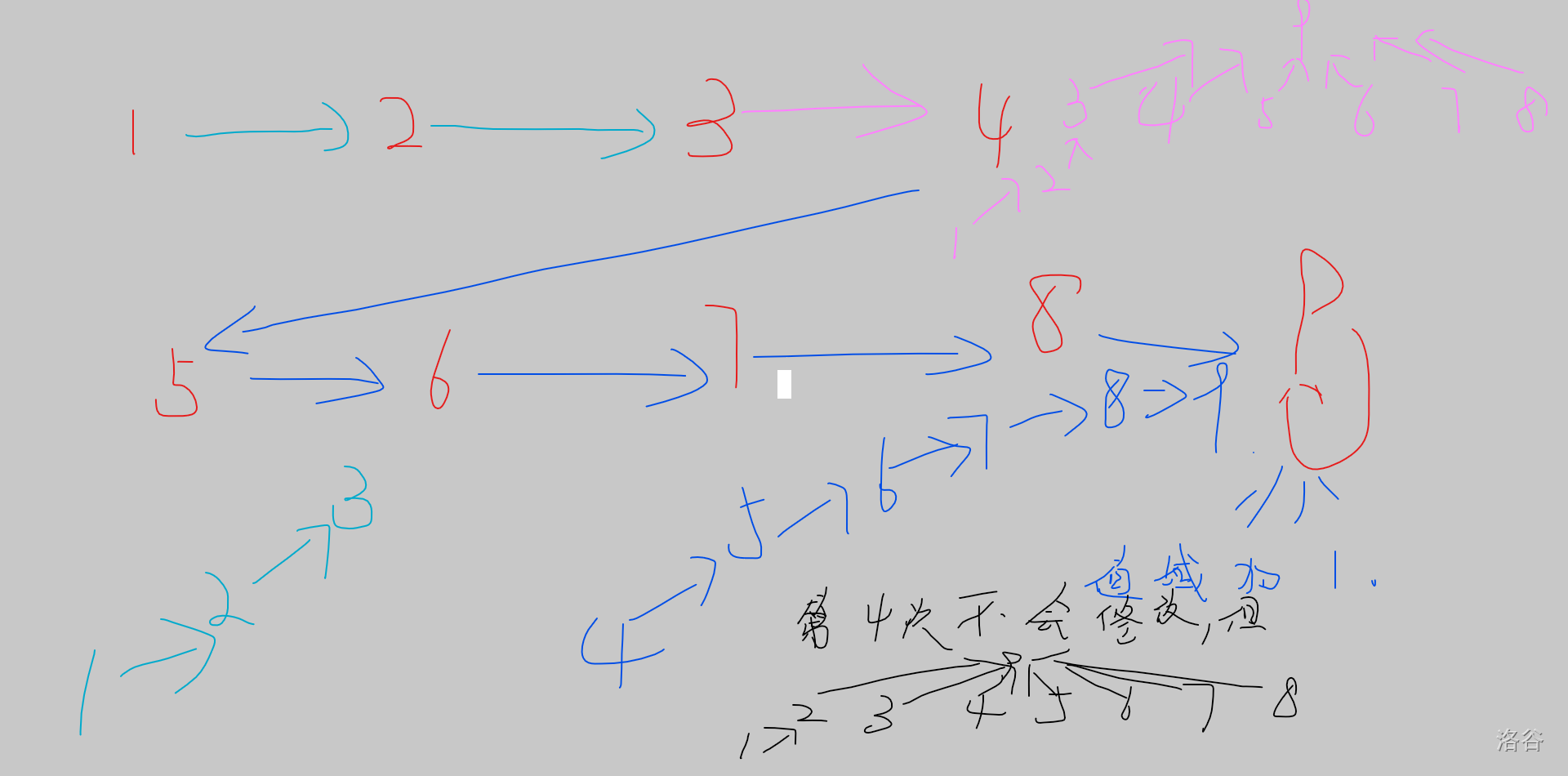
那个树一样的东西是并查集树。

可以看到效率还是特别的高哈。

如果有覆盖的值可以直接在数组上修改，反正每个点最多遍历一次。

代码：

for (int i = find (l) ; i <= r ; i = find (i + 1)){
  if (i > r) break;
  fa[i] = i + 1;
  res[i] = 需要覆盖的数;
}

这是一个典型例子，我么可以在别的地方创新一下，这里不展开。