线段树上二分

线段树上二分

下文默认你会基础线段树。

有没有读者以前打线段树模板 \(1\) 的时候，因为没开 long long 而痛失 AC 呢？

如果有，你一定觉得很可恶！

那么读者有没有想过，能不能找到一个最小的 \(p\)，使得 \(\sum\limits_{i=l}^p a_i > 2147483647\left(l\le p\le r\right)\)，从而让你爆 int 了呢？

当然先要把你的代码开成 long long 这样好做一点。

又或者说，我们把 \(2147483647\) 改成任意正整数 \(k\) 的情况下呢？那么问题就变为了：找到一个最小的 \(p\)，使得 \(\sum\limits_{i=l}^p a_i > d\left(l\le p\le r\right)\)。

这个问题看着不好做，但是如果我们钦定 \(a_i\) 非负，是不是就可以找到这个令人痛恨的位置了呢？

---

首先考虑当 \(\forall a_i \ge 0,l=1,r=n\)，并且没有修改的时候怎么做。

我们发现因为 \(a_i\) 非负，所以前缀和具有单调性，那么也可以推得 \(a_l+a_{l+1}+\cdots+a_{i} \leq a_l+a_{l+1}+\cdots+a_{i}+a_{i+1}\)（\(l\le i\le r - 1\)）。

于是我们用前缀和维护，然后二分答案就完事了。

int l = 1 ,r = n ,ans = -1/*无解*/;
// pre[i] = a[1] + a[2] + ... + a[i];
while (l <= r) {
  int mid = ((l + r) >> 1);
  if (pre[mid] - pre[l - 1] >= d) r = mid - 1 ,ans = mid;//mid 可能过头啦，可以尝试缩小右边界找可能更小的答案，但这也是可能的答案所以记录。
  else l = mid + 1;//和不够，往右边找，但是这个不可能是答案不用记录。
} writeln (ans);

然后考虑到有修改的情况。

由于前缀和修改一次最坏情况为 \(\mathcal O(n)\)，所以我们使用线段树优化它。

然后手写 query 并且二分就行了。

//线段树板子。
inline void pushdown (int u ,int l ,int r){
  if (tr[u].add) {
    int mid = ((l + r) >> 1);
    tr[u << 1].sum += (mid - l + 1) * tr[u].add ,tr[u << 1 | 1].sum += (r - mid) * tr[u].add;
    tr[u << 1].add += tr[u].add ,tr[u << 1 | 1].add += tr[u].add;
    tr[u].add = 0;
  }  
} inline int query (int u ,int l ,int r ,int ql ,int qr){
  if (l >= ql && r <= qr) return tr[u].sum;
  int mid = ((l + r) >> 1) ,res = 0;
  pushdown (u ,l ,r);
  if (ql <= mid) res = query (u << 1 ,l ,mid ,ql ,qr);
  if (mid < qr) res += query (u << 1 | 1 ,mid + 1 ,r ,ql ,qr);
  return res;
}
// 此处省略若干代码。
//----
int l = 1 ,r = n ,ans = -1;
while (l <= r) {//二分板子。
  int mid = ((l + r) >> 1);
  if (query (1 ,1 ,n ,1 ,mid) >= d) r = mid - 1 ,ans = mid;
  else l = mid + 1;
} writeln (ans);

但是这个只能称之为“线段树+二分”，而不是线段树二分！

很差劲，因为这个代码的时间复杂度最坏为 \(\mathcal O(m\log^2 n)\)，\(m\) 为操作次数。

因此我们考虑修改为 \(\mathcal O(m\log n)\)。

我们记录每一个线段树上的区间的和，然后二分，从根节点出发：

• 如果左子树的和小于 \(d\)，那么 \(p\) 一定在右子树中，此时往右子树寻找，并让 \(d\gets d - p\)，表示去除左子树区间和的影响，专心二分右子树；

• 如果左子树的和大于等于 \(d\)，那么 \(p\) 一定在左子树中，此时往左子树寻找，\(d\) 不变，因为 \(d\) 此时不受影响。

• 最后如果存在 \(p\)，那么搜到的叶节点对应的下标即为答案，因为其他的点都被排掉了。

对于无解的情况，如果 \(\sum\limits_{i=1}^n a_i < d\) 则无解。

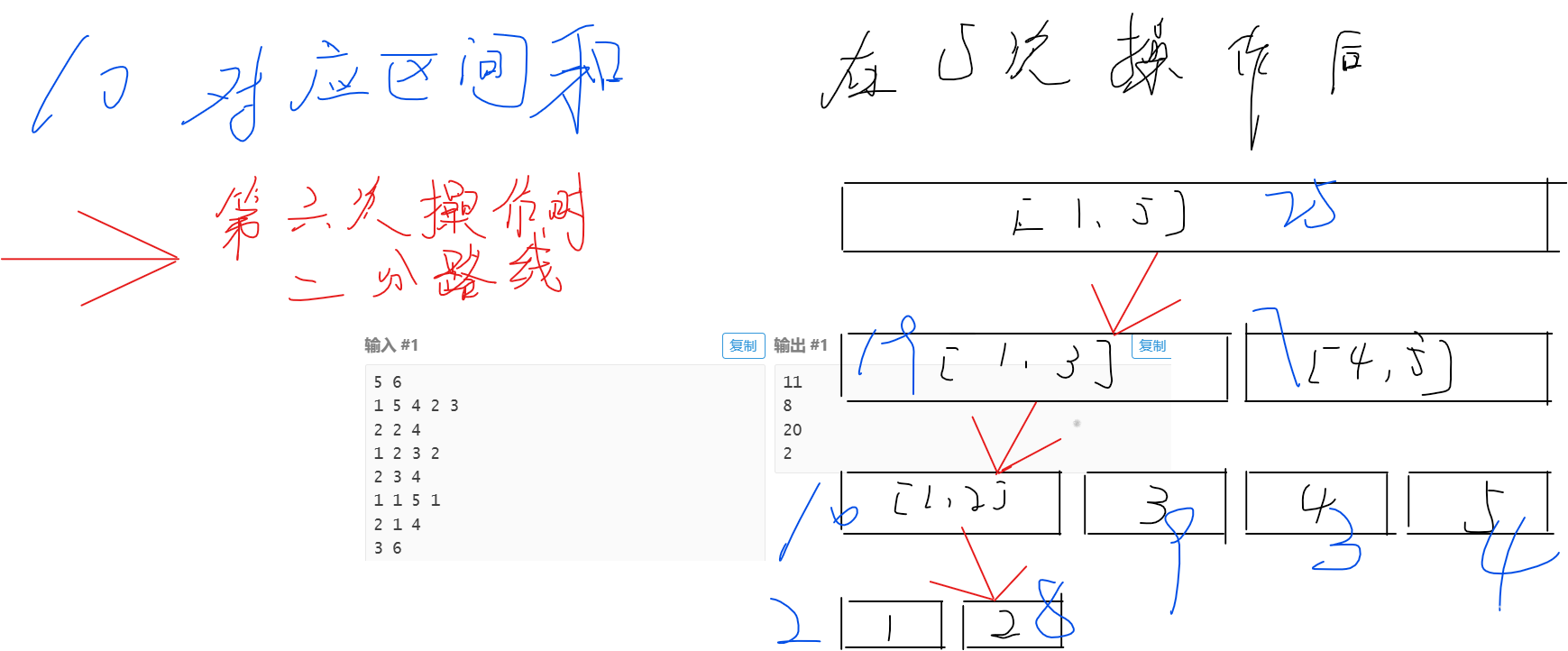
这个过程一次能够在 \(\mathcal O(\text{树高})\) 的时间复杂度解决问题，线段树树高为 \(\log n\)，所以时间复杂度为 \(\mathcal O(m\log n)\)。

这很优秀，直接吊打上面的做法。

• 线段树+二分 ； 线段树二分；

蒟蒻偶然在网上发现一道用户创建的模板题，就是这题。

inline int query_pos (int u ,int l ,int r ,int d){
  if (l == r) return l;//叶节点。
  pushdown (u ,l ,r);//注意 pushdown，因为二分时需要真实信息，而不是没有下传前的“虚假”信息。
  int mid = ((l + r) >> 1);
  if (tr[u << 1].sum < d) return query_pos (u << 1 | 1 ,mid + 1 ,r ,d - tr[u << 1].sum);//往右子树找。
  return query_pos (u << 1 ,l ,mid ,d);//答案在左子树。
}
//-----------
int d = read ();
if (tr[1].sum < d) writeln (n + 1);//无解。
else writeln (query_pos (1 ,1 ,n ,d));//直接 O(log n) 查询。

---

再看这道，它依旧是个模板题。

朴素的线段树+二分还是不够优秀。

我们运用线段树二分，因为答案呈单调性又具有修改。

维护线段树上每个区间的最大值，然后二分就可以了。

注意这题有区间限制 \(\text{询问答案}\in [l,r]\) 或者无解，需要在线段树二分的时候特别注意！

inline int query (int u ,int l ,int r ,int ql ,int qr ,int k){ 
  if (l == r) return a[l] > k ? l : -1;// a[l] > k：答案；a[l] <= k：无解（虽然其他的都排了但是这个不一定是答案，上题是把无解情况去除了所以可以直接写）。
  int mid = ((l + r) >> 1);
  if (ql <= mid && tr[u << 1].mx > k){//询问包括左儿子对应区间，并且答案在左子树中。
    int res = query (u << 1 ,l ,mid ,ql ,qr ,k);
    if (res != -1) return res;//如果这个答案不在 [l,mid] 中，即在 [1,l-1] 中，不能返回，必须递归右子树了。
  } if (mid < qr && tr[u << 1 | 1].mx > k) return query (u << 1 | 1 ,mid + 1 ,r ,ql ,qr ,k);//1.有答案，最好；2.无解，-1 返回，因为没有别的情况了。
  return -1;//qr <= mid，询问不包括右儿子对应区间，又不在左儿子对应区间，无解 -1。
}

例题讲解

MEX Queries。

好题。

首先你需要剖析三个操作的本质：

• 操作一。

  • 如果集合不包含，最后会被包含。
  • 如果集合包含，最后还是被包含。

• 所以本质就是区间覆盖成 \(1\)；

• 操作二。

  • 如果集合包含，最后会不包含。
  • 如果集合不包含，它还是不包含。

• 所以本质就是区间覆盖成 \(0\)；

• 操作三。

  • 如果集合包含，首先包含，然后又不包含了。
  • 如果集合不包含，首先包含，然后又包含。

• 所以本质就是区间反转（\(0,1\) 反转）。

• 求 MEX。

• 等价于求 \([1,10^{18}+1]\) 的第一个为 \(0\) 的正整数的值。

然后观察到这么多操作，于是想到线段树，但是 \([l,r]\) 过大，为 \(10^{18}\)，于是考虑线段树离散化，容易发现只要搞个还原数组就不会影响求 MEX 操作。

然后我们离散化了，注意：

• 加入 \(1\)，防止答案为 \(1\)；

• 加入 \(r+1\)，防止答案为某个区间的右端点加 \(1\)，但是没有包含进去。

  • 比如 \([1,2]\) 和 \([4,5]\)，离散化过后变成 \([1,2]\)，\([3,4]\)，但是实际中间还有 \([3,3]\)，答案为 \(3\)，不增加答案一不小心就 \(\color{red}{\text{WA}}\) 了！

然后考虑正确维护覆盖操作和反转操作的 lazy tag，应为覆盖的 lazy tag 先下传，因为覆盖就把反转杀了，但是反转不一定。

最后考虑“求 MEX” 操作，如果是线段树+二分，可以维护区间 \(0\) 的个数或者区间和来二分。

但是现在我们想要更优秀，于是在线段树上二分。

我们可以维护区间 \(0\) 的个数，这样更直接；但是题解区都是清一色的维护区间和 QwQ。

然后这题就以 \(\mathcal O(m\log n)\) 的时间复杂度做完了。