CF#511 Div2

A.Little C Loves 3 I

 

 1 #include <iostream>
 2 #include <cstdio>
 3 using namespace std;
 4 int n,a,b,c;
 5 int main() {
 6     scanf("%d",&n);
 7     if (n%3==0) a=b=1;
 8     else if (n%3==1) a=b=1;
 9     else a=1,b=2;
10     c=n-a-b;
11     printf("%d %d %d\n",a,b,c);
12     return 0;
13 }
View Code

 

B.Cover Points

 

 1 #include <iostream>
 2 #include <cstdio>
 3 using namespace std;
 4 int n,ans;
 5 int main() {
 6     scanf("%d",&n);
 7     for (int x,y,i=1;i<=n;i++) {
 8         scanf("%d%d",&x,&y);
 9         ans=max(ans,x+y);
10     }
11     printf("%d\n",ans);
12     return 0;
13 }
View Code

 

C.Enlarge GCD

题意：去掉最少的数使得$gcd$变大

做法：先将所有数除一个$gcd$，这样只需要知道含有某个质因子的数有多少个，将剩下的去掉即为一组可行解。不过可以预处理每个数的最小质因子，这样将分解质因数的时间代价降为$O(log_{2}n)$

 

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <algorithm>
 4 using namespace std;
 5 const int N=300010;
 6 const int S=15000001;
 7 int n,cnt; int a[N];
 8 int pri[S],mi[S],sum[S]; bool mark[S];
 9 int gcd(int x,int y) {
10     if (!y) return x;
11     return gcd(y,x%y);
12 }
13 void pre() {
14     for (int i=2;i<S;i++) {
15         if (!mark[i])
16             mi[i]=++cnt,pri[cnt]=i;
17         for (int j=1;j<=cnt;j++) {
18             if (i*pri[j]>=S) break;
19             mark[i*pri[j]]=1;
20             mi[i*pri[j]]=j;
21             if (i%pri[j]==0) break;
22         }
23     }
24     return;
25 }
26 void read() {
27     scanf("%d",&n);
28     for (int i=1;i<=n;i++)
29         scanf("%d",&a[i]);
30     int t=0;
31     for (int i=1;i<=n;i++)
32         t=gcd(t,a[i]);
33     for (int i=1;i<=n;i++)
34         a[i]/=t;
35     return;
36 }
37 bool judge() {
38     for (int i=1;i<=n;i++)
39         if (a[i]!=1)
40             return false;
41     return true;
42 }
43 void work() {
44     if (judge()) {
45         printf("-1\n");
46         return;
47     }
48     for (int i=1;i<=n;i++) {
49         int last=0;
50         while(a[i]!=1) {
51             int t=mi[a[i]];
52             if (t!=last)
53                 last=t,sum[t]++;
54             a[i]/=pri[t];
55         }
56     }
57     int ans=n-1;
58     for (int i=1;i<=cnt;i++)
59         ans=min(ans,n-sum[i]);
60     printf("%d\n",ans);
61     return;
62 }
63 int main() {
64     pre();
65     read();
66     work();
67     return 0;
68 }
View Code

 

D.Little C Loves 3 II

题意：棋盘上曼哈顿距离为$3$的位置可以俩俩匹配，问最多多少个格子匹配

做法：比赛的时候先写了一个匈牙利算法跑暴力，调了很长时间，然后试了一会找到规律

 

 1 #include <iostream>
 2 #include <cstdio>
 3 using namespace std;
 4 typedef long long ll;
 5 ll n,m;
 6 int main() {
 7     scanf("%I64d%I64d",&n,&m);
 8     if (n>m) swap(n,m);
 9     if (n==1) {
10         ll t1=m/6,t2=max(0ll,m%6-3);
11         printf("%I64d\n",t1*6+t2*2);
12     }
13     else if (n==2) {
14         if (m==2) printf("0\n");
15         else if (m==3) printf("4\n");
16         else if (m==7) printf("12\n");
17         else printf("%I64d\n",n*m);
18     }
19     else {
20         if (n&1) swap(n,m);
21         if (n&1) printf("%I64d\n",n*m-1);
22         else printf("%I64d\n",n*m);
23     }
24     return 0;
25 }
View Code

 

E.Region Separation

题意：给出一棵树，点有点权，要划分为若干个级别，每个级别都将整棵树分为若干个点权和相等的连通块，要求每个级别的连通块都是对上一级别的连通块内划分，求方案数

题意比较难懂，给个样例解释一下

 

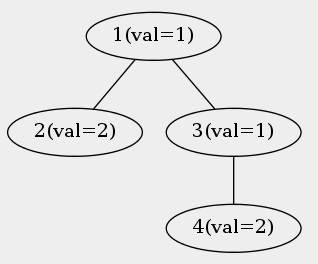
$ans=3$

$Plan A: level1\ \left\{1,2,3,4\right\}$

$Plan B: level1\ \left\{1,2,3,4\right\}\ level2\ \left\{1,2\right\},\left\{3,4\right\}$

$Plan C:level1\ \left\{1,2,3,4\right\},\ levle2\ \left\{1,3\right\},\left\{2\right\},\left\{4\right\}$

做法：考虑将整棵树分为$k$个区域，定义用$s_{i}$表示第$i$个点的子树权值和，$1$为根

那么一定存在$k$个点满足$s_{i} \equiv 0 mod \frac{s_{1}}{k}$，那么若点$i$满足$k$划分，那么一定满足

$k=\frac{x*s_{1}}{s_{i}}, x$为正整数，所以$k$中含有因子$\frac{s_{1}}{s_{1}/s_{n}}$，即这个点可能对该划分有贡献

那么统计每个点都可能对哪些数量的划分有贡献，再考虑统计方案数

如果可以划分为$k$块，那么按照$plan$的区分方式，会对$k*x$块的方案有贡献，因此累加俩个dp数组

$f[i]$表示有多少点可以对$i$划分有贡献

$g[i]$表示$i$划分有多少方案数

 

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int N=1000010;
const int mod=1000000007;
int n,ans;
int a[N],p[N],f[N],g[N];
ll s[N];
ll gcd(ll x,ll y) {
    if (!y) return x;
    return gcd(y,x%y);
}
int main() {
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
        scanf("%d",&a[i]),s[i]=a[i];
    for (int i=2;i<=n;i++)
        scanf("%d",&p[i]);
    for (int i=n;i>1;i--)
        s[p[i]]+=s[i];
    for (int i=1;i<=n;i++) {
        ll t=s[1]/gcd(s[1],s[i]);
        if (t<=n) f[t]++;
    }
    for (int i=n;i>=1;i--)
    for (int j=i*2;j<=n;j+=i)
        f[j]+=f[i];
    g[1]=1;
    for (int i=1;i<=n;i++)
        if (f[i]==i) {
            (ans+=g[i])%=mod;
            for (int j=2*i;j<=n;j+=i)
                (g[j]+=g[i])%=mod;
        }
    printf("%d\n",ans);
    return 0;
}
View Code

 

posted @ 2018-09-22 08:55  2018szb  阅读(103)  评论(0)    收藏  举报