基础算法
折半搜索
折半搜索(双向搜索),又称 \(meet\space in\space the\space middle\)。
这种搜索就是从初态和终态出发各搜索一半状态,产生两颗深度减半的搜索树,在中间交会、组合成最终的答案。
面对一些使用dfs或bfs难以解决的题,我们可以使用折半搜索。
在一些时间复杂度为 \(O(2^n)\) 的做法中,可以用折半搜索使其时间复杂度变为 \(O(2*2^{\frac n2})\)
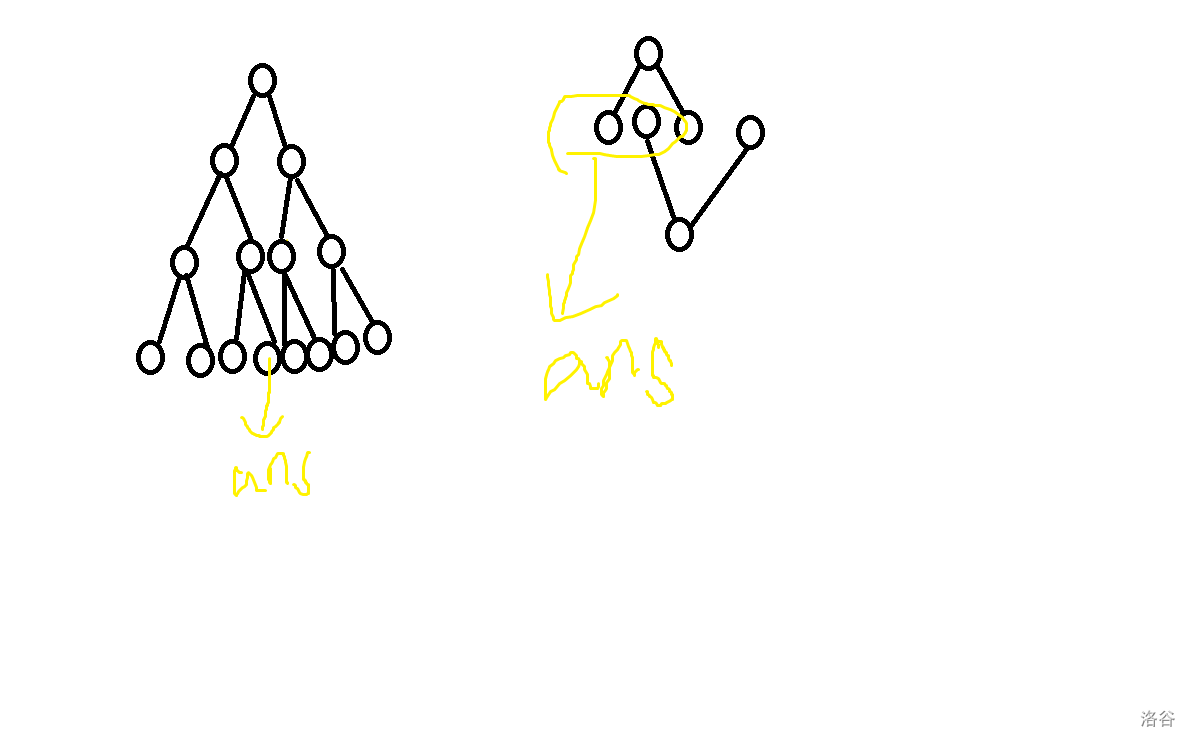
例如这幅图,左侧是直接进行一次搜索产生的搜索树,右侧是双向搜索的两棵搜索树,显然的,双向搜索避免了层数过深时分支数量大规模增长。
注意:在很多折半搜索题目中题目中都需要用到二分,用来组合最终答案。
深搜
P4799 [CEOI 2015] 世界冰球锦标赛 (Day2)
一道非常经典的折半搜索题,只要求出前一半的所有可能情况和后一半的所有可能情况,二分一下即可。
code
#include <bits/stdc++.h>
using namespace std;
long long n,m;
long long cnt1,cnt2,a[50],b[1100010],c[1100010];
void dfs1(int k,long long cur)
{
if(cur>m) return;
if(k==n/2+1)
{
b[++cnt1]=cur;
return;
}
dfs1(k+1,cur);
dfs1(k+1,cur+a[k]);
}
void dfs2(int k,long long cur)
{
if(cur>m) return;
if(k==n/2)
{
c[++cnt2]=cur;
return;
}
dfs2(k-1,cur);
dfs2(k-1,cur+a[k]);
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
dfs1(1,0);
dfs2(n,0);
sort(c+1,c+cnt2+1);
long long ans=0;
for(int i=1;i<=cnt1;i++)
{
int t=upper_bound(c+1,c+cnt2+1,m-b[i])-c;
ans+=(long long)t-1;
}
cout<<ans<<endl;
return 0;
}
P3067 [USACO12OPEN] Balanced Cow Subsets G
这个题可以说是上一题的加强版
首先,暴搜 \(O(3^n)\) 显然不行
每只奶牛只有三种情况,放A/放B/不放
设前一半放在 \(A\) 组中的有 \(a_1\) 个,放在 \(B\) 组中的有 \(b_1\) 个;后一半放在 \(A\) 组中的有 \(a_2\) 个,放在 \(B\) 组中的有 \(b_2\) 个。
依题得 \(a_1+a_2=b_1+b_2\)
移项得 \(a_1-b_1=b_2-a_2\)
统计前一半 \(a_1-b_1\) 的方案,看看有没有后一半的 \(b_2-a_2\) 与之相等。
折半搜索即可。
#include <bits/stdc++.h>
using namespace std;
#define For(i,x,y,...) for(int i=(x),##__VA_ARGS__;i<=(y);++i)
#define foR(i,x,y,...) for(int i=(x),##__VA_ARGS__;i>=(y);--i)
#define Rep(i,x,y,...) for(int i=(x),##__VA_ARGS__;i<(y);++i)
#define endl '\n'
#define debug(...)
#define debug1(a,i,...) cout<<i<<" "<<a[i]<<endl;
typedef long long ll;
#define fi first
#define se second
#define PII pair<int,int>
#define me(s,x) memset(s,x,sizeof s)
#define pb emplace_back
#define LOCAL
template<typename T>ostream&operator<<(ostream&os,const vector<T>&v)
{
os<<"[";
for(int i=0;i<v.size();++i){os<<v[i];if(i!=v.size()-1)os<<", ";}
os<<"]";
return os;
}
template<typename T>ostream&operator<<(ostream&os,const set<T>&s){
os<<"{";bool first=1;
for(const auto&x:s){if(!first)os<<", ";os<<x;first=0;}
os<<"}";
return os;
}
template<typename K,typename V>ostream&operator<<(ostream&os,const map<K,V>&m){
os<<"{";bool first=1;
for(const auto&p:m){if(!first)os<<", ";os<<p.fi<<":"<<p.se;first=0;}
os<<"}";
return os;
}
template<typename A,typename B>ostream&operator<<(ostream&os,const pair<A,B>&p){
return os<<"("<<p.fi<<", "<<p.se<<")";
}
#ifdef LOCAL
#define debug(...) cerr<<"["<<#__VA_ARGS__<<"]:",debug_out(__VA_ARGS__)
void debug_out(){cerr<<endl;}
template<typename Head,typename... Tail>
void debug_out(Head H,Tail... T){
cerr<<" "<<H;
debug_out(T...);
}
#else
#define debug(...) 42
#endif
template<typename T=int>T read(){T x;cin>>x;return x;}
const int mod=20140921;
struct mint{
int x;mint(int x=0):x(x<0?x+mod:x<mod?x:x-mod){}
mint(ll y){y%=mod,x=y<0?y+mod:y;}
mint& operator += (const mint &y){x=x+y.x<mod?x+y.x:x+y.x-mod;return *this;}
mint& operator -= (const mint &y){x=x<y.x?x-y.x+mod:x-y.x;return *this;}
mint& operator *= (const mint &y){x=1ll*x*y.x%mod;return *this;}
friend mint operator + (mint x,const mint &y){return x+y;}
friend mint operator - (mint x,const mint &y){return x-y;}
friend mint operator * (mint x,const mint &y){return x*y;}
};mint Pow(mint x,ll y=mod-2){mint z(1);for(;y;y>>=1,x*=x)if(y&1)z*=x;return z;}
const int N=25;
int a[N],ans;
bool vis[1<<N];
int n,tot;
map<ll,int> mp;
vector<int> v[1<<N];
void dfs1(int u,ll sum,int used){
if(u==n/2+1){
if(!mp.count(sum)) mp[sum]=++tot;
v[mp[sum]].pb(used);
return;
}
dfs1(u+1,sum+a[u],used|(1<<(u-1)));
dfs1(u+1,sum-a[u],used|(1<<(u-1)));
dfs1(u+1,sum,used);
}
void dfs2(int u,ll sum,int used){
if(u==n/2){
if(mp[sum]){
for(auto x:v[mp[sum]]) if(!vis[x|used]&&x|used!=0) vis[x|used]=1,ans++;
}
return;
}
dfs2(u-1,sum+a[u],used|(1<<(u-1)));
dfs2(u-1,sum-a[u],used|(1<<(u-1)));
dfs2(u-1,sum,used);
}
void MAIN(){
cin>>n;
For(i,1,n) cin>>a[i];
dfs1(1,0,0);dfs2(n,0,0);
cout<<ans<<endl;
}signed main(){
int t=1;while(t--){
MAIN();
}
return 0;
}
于是这道蓝题就被轻松拿下了。
P12878[蓝桥杯 2025 国 C] 拔河
提答题。
考虑折半搜索,显然前一半后一半都有正或负的可能,所以枚举前一半后在后一半中二分其相反数即可。
答案为 **66
NFLS 最大取模子集
考虑折半搜索,在枚举完前一半和后一半的和后,我们需要二分,有一个比较显然的结论:
对于 \(p,a,b<m,p+a<m,p+b>m\),记\(x\equiv p+b(mod\space m)\) ,则有 \(p+a>x\)。
证明:反证,若不然。
\(\therefore p+a\leq x\)
\(\because p,b<m\)
\(\therefore x=p+b-m\)
\(\therefore p+a\leq p+b-m\)
\(\therefore a\leq b-m\)
\(\therefore a+m\leq b\)
又\(a>0,b<m\)
\(\therefore\) 矛盾
\(\therefore p+a>x\)
\(\Box\)
所以对于每一个前一半的 \(p\),只需找后半段最大的 \(a\),使得 \(p+a<m\) 即可。
For(i,1,cnt1){
int p=lower_bound(p2+1,p2+cnt2+1,m-p1[i])-p2;
--p;
ans=max(ans,p1[i]+p2[p]);
}
[ABC271F] XOR on Grid Path
注意到 \(a \oplus a=0\),只需找前一半和后一半相同的数即可。
注意下标,及是否“包括”。
CF912E Prime Gift
一道比较有实力的折半搜索,很好的折半搜索+二分。
这里的折半搜索有个技巧,如果我们直接分两半很容易爆long long,因此我们尽量均分两组数,可以把数组排序之后奇数和偶数进行分组。
接下来就是二分。check函数是一个双指针,\(l\) 就代表 能使 \(x+v2[l]<=mid\) 的最大的下标。
最后和 \(k\) 比较即可。
#include <bits/stdc++.h>
using namespace std;
#define For(i,x,y,...) for(int i=(x),##__VA_ARGS__;i<=(y);++i)
#define foR(i,x,y,...) for(int i=(x),##__VA_ARGS__;i>=(y);--i)
#define Rep(i,x,y,...) for(int i=(x),##__VA_ARGS__;i<(y);++i)
#define endl '\n'
#define debug(...)
#define debug1(a,i,...) cout<<i<<" "<<a[i]<<endl;
typedef long long ll;
#define fi first
#define se second
#define PII pair<int,int>
#define me(s,x) memset(s,x,sizeof s)
#define pb emplace_back
#define LOCAL
template<typename T>ostream&operator<<(ostream&os,const vector<T>&v)
{
os<<"[";
for(int i=0;i<v.size();++i){os<<v[i];if(i!=v.size()-1)os<<", ";}
os<<"]";
return os;
}
template<typename T>ostream&operator<<(ostream&os,const set<T>&s){
os<<"{";bool first=1;
for(const auto&x:s){if(!first)os<<", ";os<<x;first=0;}
os<<"}";
return os;
}
template<typename K,typename V>ostream&operator<<(ostream&os,const map<K,V>&m){
os<<"{";bool first=1;
for(const auto&p:m){if(!first)os<<", ";os<<p.fi<<":"<<p.se;first=0;}
os<<"}";
return os;
}
template<typename A,typename B>ostream&operator<<(ostream&os,const pair<A,B>&p){
return os<<"("<<p.fi<<", "<<p.se<<")";
}
#ifdef LOCAL
#define debug(...) cerr<<"["<<#__VA_ARGS__<<"]:",debug_out(__VA_ARGS__)
void debug_out(){cerr<<endl;}
template<typename Head,typename... Tail>
void debug_out(Head H,Tail... T){
cerr<<" "<<H;
debug_out(T...);
}
#else
#define debug(...) 42
#endif
template<typename T=int>T read(){T x;cin>>x;return x;}
const int mod=20140921;
struct mint{
int x;mint(int x=0):x(x<0?x+mod:x<mod?x:x-mod){}
mint(ll y){y%=mod,x=y<0?y+mod:y;}
mint& operator += (const mint &y){x=x+y.x<mod?x+y.x:x+y.x-mod;return *this;}
mint& operator -= (const mint &y){x=x<y.x?x-y.x+mod:x-y.x;return *this;}
mint& operator *= (const mint &y){x=1ll*x*y.x%mod;return *this;}
friend mint operator + (mint x,const mint &y){return x+y;}
friend mint operator - (mint x,const mint &y){return x-y;}
friend mint operator * (mint x,const mint &y){return x*y;}
};mint Pow(mint x,ll y=mod-2){mint z(1);for(;y;y>>=1,x*=x)if(y&1)z*=x;return z;}
const int N=20;
#define int unsigned long long
int p[N];
vector<int> v1,v2;
int n,k;
void dfs1(int u,int sum){
if(u>n){
v1.pb(sum);
return;
}
for(int i=1;;i*=1ll*p[u]){
if(sum>1e18/i) break;
dfs1(u+2,sum*i);
}
}
void dfs2(int u,int sum){
if(u>n){
v2.pb(sum);
return;
}
for(int i=1;;i*=1ll*p[u]){
if(sum>1e18/i) break;
dfs2(u+2,sum*i);
}
}
bool chk(int mid){//<=mid
int l=v2.size()-1;
int res=0;
for(auto x:v1){
if(x>mid) break;
while(l>=0&&mid/v2[l]<x) --l;
res+=l+1;
}
return res<k;
}
void MAIN(){
cin>>n;
For(i,1,n) cin>>p[i];
cin>>k;
sort(p+1,p+n+1);
dfs1(1,1),dfs2(2,1);
sort(v1.begin(),v1.end()),sort(v2.begin(),v2.end());
int l=1,r=1e18,ans=0;
while(l<=r){
int mid=l+r>>1;
if(chk(mid)){
l=mid+1;
}
else{
r=mid-1;
ans=mid;
}
}
cout<<ans<<endl;
}signed main(){
int t=1;while(t--){
MAIN();
}
return 0;
}
广搜
P10487 Nightmare II
一道比较有实力的bfs双向搜索。
还是比较板的
有几个需要注意的地方:
-
要保证两人 同时 行走。
-
男生走的时候不能只看终点,还要看路径上的点有没有鬼魂。
-
在一个点走到另一个点后,有可能到达的点上一步还没有鬼魂,下一步还没走就有了,遇到这种情况这个点就不能再走了。
4.2k代码,仅供参考(我觉得没人会愿意抄的)。
#include <bits/stdc++.h>
using namespace std;
#define For(i,x,y,...) for(int i=(x),##__VA_ARGS__;i<=(y);++i)
#define foR(i,x,y,...) for(int i=(x),##__VA_ARGS__;i>=(y);--i)
#define Rep(i,x,y,...) for(int i=(x),##__VA_ARGS__;i<(y);++i)
#define endl '\n'
typedef long long ll;
#define fi first
#define se second
#define PII pair<int,int>
#define me(s,x) memset(s,x,sizeof s)
#define pb emplace_back
#define LOCAL
template<typename T>ostream&operator<<(ostream&os,const vector<T>&v)
{
os<<"[";
for(int i=0;i<v.size();++i){os<<v[i];if(i!=v.size()-1)os<<", ";}
os<<"]";
return os;
}
template<typename T>ostream&operator<<(ostream&os,const set<T>&s){
os<<"{";bool first=1;
for(const auto&x:s){if(!first)os<<", ";os<<x;first=0;}
os<<"}";
return os;
}
template<typename K,typename V>ostream&operator<<(ostream&os,const map<K,V>&m){
os<<"{";bool first=1;
for(const auto&p:m){if(!first)os<<", ";os<<p.fi<<":"<<p.se;first=0;}
os<<"}";
return os;
}
template<typename A,typename B>ostream&operator<<(ostream&os,const pair<A,B>&p){
return os<<"("<<p.fi<<", "<<p.se<<")";
}
#ifdef LOCAL
#define debug(...) cerr<<"["<<#__VA_ARGS__<<"]:",debug_out(__VA_ARGS__)
void debug_out(){cerr<<endl;}
template<typename Head,typename... Tail>
void debug_out(Head H,Tail... T){
cerr<<" "<<H;
debug_out(T...);
}
#else
#define debug(...) 42
#endif
template<typename T=int>T read(){T x;cin>>x;return x;}
const int mod=1e9+7;
struct mint{
int x;mint(int x=0):x(x<0?x+mod:x<mod?x:x-mod){}
mint(ll y){y%=mod,x=y<0?y+mod:y;}
mint& operator += (const mint &y){x=x+y.x<mod?x+y.x:x+y.x-mod;return *this;}
mint& operator -= (const mint &y){x=x<y.x?x-y.x+mod:x-y.x;return *this;}
mint& operator *= (const mint &y){x=1ll*x*y.x%mod;return *this;}
friend mint operator + (mint x,const mint &y){return x+y;}
friend mint operator - (mint x,const mint &y){return x-y;}
friend mint operator * (mint x,const mint &y){return x*y;}
};mint Pow(mint x,ll y=mod-2){mint z(1);for(;y;y>>=1,x*=x)if(y&1)z*=x;return z;}
const int N=805;
char c[N][N];
bool vis1[N][N],vis2[N][N];
int n,m;
int zx1,zy1,zx2,zy2,sx1,sy1,sx2,sy2;
struct no{
int x,y,dis;
};
int dx[]={0,1,-1,0,0},dy[]={0,0,0,1,-1};
queue<no> q1,q2;
bool in(int t,int x,int y){
return abs(zx1-x)+abs(zy1-y)<=2*t||abs(zx2-x)+abs(zy2-y)<=2*t;
}
bool chk(int x,int y){
return x>=1&&x<=n&&y>=1&&y<=m&&c[x][y]!='X';
}
vector<PII> v;
int bfs(){
q1.push({sx1,sy1,0});
q2.push({sx2,sy2,0});
vis1[sx1][sy1]=vis2[sx2][sy2]=1;
while(!q1.empty()&&!q2.empty()){
ll t=q1.front().dis;
v.clear();
while(!q1.empty()&&q1.front().dis==t){
if(in(t+1,q1.front().x,q1.front().y)){
q1.pop();continue;
}
v.push_back({q1.front().x,q1.front().y});
q1.pop();
}
for(auto &[x,y]:v){
For(i,0,4)For(j,0,4)For(k,0,4){
int nx=x+dx[i]+dx[j]+dx[k],ny=y+dy[i]+dy[j]+dy[k];
if(nx==x&&ny==y) continue;
if(in(t+1,x+dx[i],y+dy[i])||in(t+1,x+dx[i]+dx[j],y+dy[i]+dy[j])||in(t+1,nx,ny)) continue;
if(!chk(x+dx[i],y+dy[i])||!chk(x+dx[i]+dx[j],y+dy[i]+dy[j])||!chk(nx,ny)||vis1[nx][ny]) continue;
if(vis2[nx][ny]){
return t+1;
}
vis1[x+dx[i]][y+dy[i]]=vis1[x+dx[i]+dx[j]][y+dy[i]+dy[j]]=vis1[nx][ny]=1;
q1.push({nx,ny,t+1});
vis1[nx][ny]=1;
}
}
v.clear();
while(!q2.empty()&&q2.front().dis==t){
if(in(t+1,q2.front().x,q2.front().y)){
q2.pop();continue;
}
v.push_back({q2.front().x,q2.front().y});
q2.pop();
}
for(auto &[x,y]:v){
For(i,1,4){
int nx=x+dx[i],ny=y+dy[i];
if(nx<1||nx>n||ny<1||ny>m||c[nx][ny]=='X'||vis2[nx][ny]||in(t+1,nx,ny)) continue;
if(vis1[nx][ny]){
return t+1;
}
q2.push({nx,ny,t+1});
vis2[nx][ny]=1;
}
}
}
return -1;
}
void MAIN(){
zx1=0;
while(!q1.empty()) q1.pop();
while(!q2.empty()) q2.pop();
me(vis1,0),me(vis2,0);
cin>>n>>m;
For(i,1,n){
For(j,1,m){
cin>>c[i][j];
if(c[i][j]=='Z'){
if(!zx1) zx1=i,zy1=j;
else zx2=i,zy2=j;
}
if(c[i][j]=='M') sx1=i,sy1=j;
if(c[i][j]=='G') sx2=i,sy2=j;
}
}
cout<<bfs()<<endl;
}signed main(){
int t=read();while(t--){
MAIN();
}
return 0;
}
P2324 [SCOI2005] 骑士精神
将矩阵转换为字符串,可以用map判重,进行双向 \(bfs\)。
在放入 \(8\) 步之后,如果最后大于 \(15\),就输出 -1。
顺便提一句,这个题 \(A*\)、\(IDA*\) 或者 \(IDDFS\) 也很好写,有兴趣的同学可以学一下。
其实这几个算法都是互通的。
并查集
并查集(Union-Find)是一种用于处理不相交集合的合并与查询问题的数据结构。
并查集包括如下两个基本操作:
-
\(find(x)\):查找元素 x 所属集合的根节点。
-
\(union(x, y)\):合并 x 和 y 所属的两个集合。
为了实现这种数据结构,我们通常会使用“代表元法”,即为每个集合选择一个固定的元素作为整个集合的“代表”。
通俗点讲,就是每个小组中选择一个小组长作为这个小组的代表。
显然的,我们可以用一个树形结构存储每个集合,树上的每个节点都是一个元素,而每个集合的代表就是这棵树的根。
我们可以维护一个数组 \(fa\) 来保存 \(x\) 的父节点,令树根的 \(fa\) 值为它自己。
在合并两个集合时,就可将两棵树的根 \(root1\) 和 \(root2\) 进行合并,将其中一个根作为另一个根的子节点,即为 \(fa[root1]=root2\)
初始化 时,每个点都属于一个单独的集合,表示一棵只有根的树,因此,我们把每个节点的父亲都设为它自己。
而在 查询 时,我们需要递归 \(fa\) 来找到根节点,这样的查询效率太低,为了提高查询效率,我们可以采用路径压缩和按秩合并两种思想。
路径压缩与按秩合并
比较显然的是,我们为了提高效率,可以直接在每个 \(fa\) 中存储这个元素所在集合的代表,我们只关心树的根节点而不关心树的形态,那么我们就可以将树上的每个节点与根节点直接相连。
这是 oiwiki 上的图,大家可以结合图片理解一下。
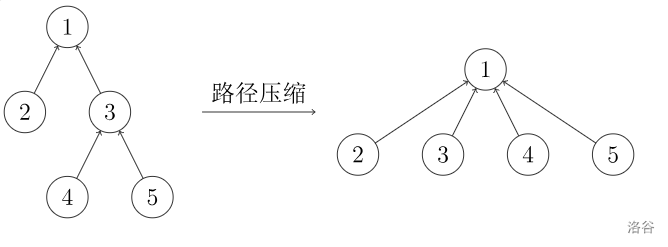
显然的,上图左右两棵树在并查集中是等价的。
实现上,我们可以在每次执行 find 操作时,把访问的每个节点都指向树根。
这种优化方法叫 路径压缩。
按秩合并 的“秩”有两种定义,一种是树在未路径压缩前的深度,另一种是集合大小。在“秩”表示集合大小的时候,又叫 启发式合并 。
按秩合并就是将“小结构”合并到“大结构”中,它只会增加小集合的查询代价,复杂度较优。
因为启发式合并相对比较好写,所以我们一般会写启发式合并。
启发式合并具体来说,则是对每个根都维护一个 \(size(x)\),每次将 \(size\) 小的合并到大的上面。
只使用路径压缩,或只使用按秩合并,时间复杂度都是 \(O(m\log n)\)。
一般来说,只是用路径压缩,不使用启发式合并也是可以的。
for(int i=1;i<=n;++i) fa[i]=i;//初始化
int find(int u){return fa[u]==u?u:fa[u]=find(fa[u]);}//路径压缩
void unionn(int x,int y){
int p=find(x),q=find(y);
if(p==q) return;
if(siz[p]>siz[q]) swap(p,q);//启发式合并
siz[q]+=siz[p];//启发式合并
fa[p]=q;//合并
}
P1551 亲戚
一道很水的并查集板子。
甚至不需要路径压缩。
P3367【模板】并查集
使用路径压缩即可。
种胡萝卜
月赛题。
每个点的父亲指向这个点前面最近的未标记点。
设答案为 \(ans\) 每次合并 \(ans\),\(ans-1\)即可。
时间复杂度 \(O(n\space log\space n)\)
注意到 \(n<=3\times10^6\) 大概跑 \(6\times 10^7\) 次,所以要使用较快的输入输出方式。
道路评价
nfls 模拟赛题。
一个比较显然的性质:
按w排序,然后求以这条边为最大的数量和减去以这条边为最小的数量和。
P1196 [NOI2002] 银河英雄传说
比较有水平的一道 带权并查集。
很显然,其他操作都是板子,只有回答询问。
考虑暴力,一个一个扫,显然超时。
显然可以前缀和来求。
如果不在一个连通块内,输出 -1 即可。
维护一下每个节点到队头的距离,一个节点到一个新队头的距离就是这个点到旧队头的距离加新队头和旧队头的距离。递归求解即可。
合并的时候旧队列加上新队列的大小即可。
最后输出 \(len_x-len_y-1\) 即可,记得一定要减一,题目问的是两个点 之间 的数量。
P1955 [NOI2015] 程序自动分析
先做 \(e=1\) 的操作,再做 \(e=0\) 的操作,相等就合并。
判不等的时候,只要在一个连通块内,就输出 NO。
注意到 \(1\leq i,j\leq 10^9\),需要离散化。
P2024 [NOI2001] 食物链
生成树
给定一张边带权的有 \(n\) 个顶点,\(m\) 条边的无向图 \(G\)。由全部 \(n\) 个顶点和 \(n-1\) 条边构成的无向联通子图被称为 \(G\) 的一棵生成树。边的权值之和最小的生成树被称为无向图 \(G\) 的最小生成树。
最小生成树(MST)
前置知识
- 树
- 并查集
- 生成树
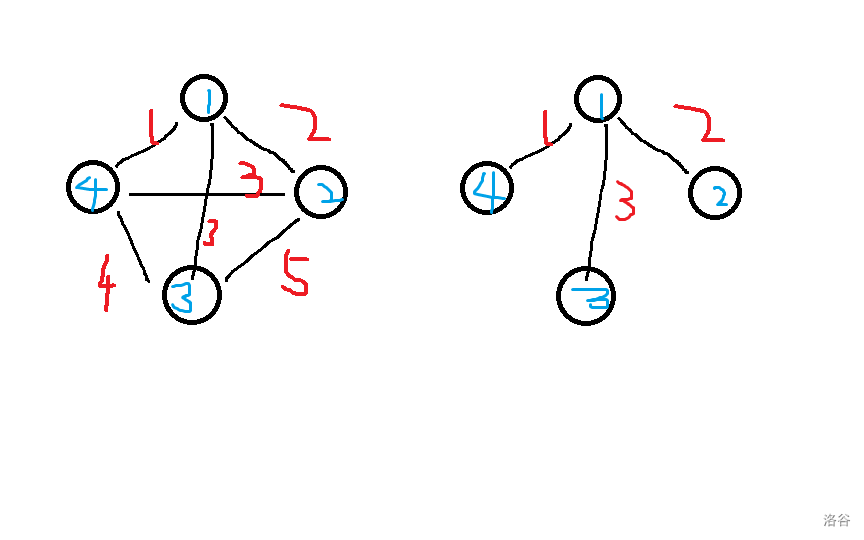
如上图,左图的最小生成树是右边的图,边权之和为 \(6\),并且没有方案使得其他生成树权值之和比 \(6\) 小。
最小生成树的常见算法主要有两种:Kruskal 和 Prim 算法。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号