白话数据结构之【最小生成树】（转载）

原文：https://blog.csdn.net/u013445530/article/details/42811635

一：基本概念

 

1：什么是生成树？

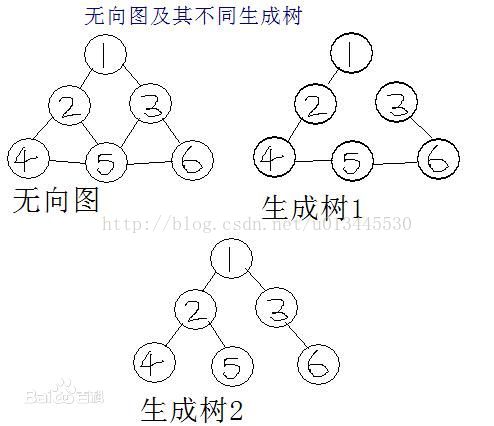
对于图G<V,E>,如果其子图G'<V',E'>满足V'=V，且G'是一棵树，那么G'就是图G的一颗生成树。生成树是一棵树，按照树的定义，每个顶点都能访问到任何一个其它顶点。（离散数学中的概念），其中V是顶点，E是边，通俗来讲生成树必须包含原图中的所有节点且是连通的

比如

 

2：最小生成树

一个无向连通图G=(V,E)，最小生成树就是联结所有顶点的边的权值和最小时的子图T，此时T无回路且连接所有的顶点，所以它必须是棵树。就是将原图的n个顶点用

n-1条边的权值夹起来最小的且连通没有回路的图

 

 

二：求法

 

 

最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出

 

 

Prim（普里姆）算法

 

MST（Minimum Spanning Tree，最小生成树）问题有两种通用的解法，Prim算法就是其中之一，它是从点的方面考虑构建一颗MST，大致思想是：设图G顶点集合为U，首先任意选择图G中的一点作为起始点a，将该点加入集合V，再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小，此时将b点也加入集合V；以此类推，现在的集合V={a，b}，再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小，此时将c点加入集合V，直至所有顶点全部被加入V，此时就构建出了一颗MST。因为有N个顶点，所以该MST就有N-1条边，每一次向集合V中加入一个点，就意味着找到一条MST的边。

 

用图示和代码说明：

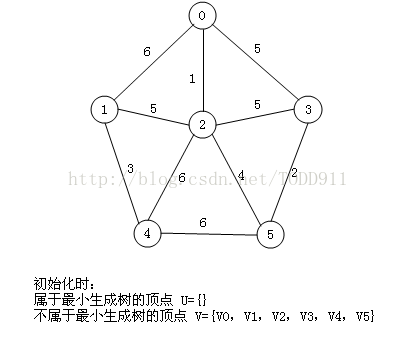
初始状态：

设置2个数据结构：

lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST

mst[i]:表示对应lowcost[i]的起点，即说明边<mst[i],i>是MST的一条边，当mst[i]=0表示起点i加入MST

 

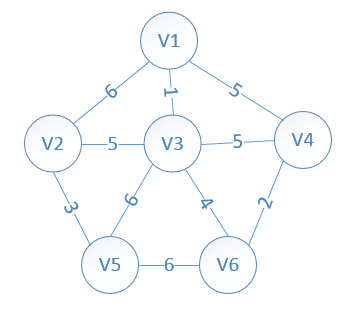
我们假设V1是起始点，进行初始化（*代表无限大，即无通路）：

 

lowcost[2]=6，lowcost[3]=1，lowcost[4]=5，lowcost[5]=*，lowcost[6]=*

mst[2]=1，mst[3]=1，mst[4]=1，mst[5]=1，mst[6]=1，（所有点默认起点是V1）

 

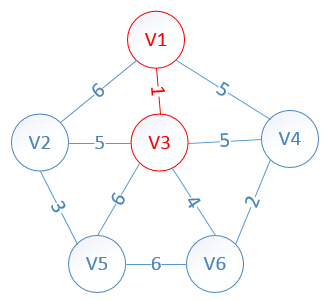
明显看出，以V3为终点的边的权值最小=1，所以边<mst[3],3>=1加入MST

此时，因为点V3的加入，需要更新lowcost数组和mst数组：

 

lowcost[2]=5，lowcost[3]=0，lowcost[4]=5，lowcost[5]=6，lowcost[6]=4

mst[2]=3，mst[3]=0，mst[4]=1，mst[5]=3，mst[6]=3

 

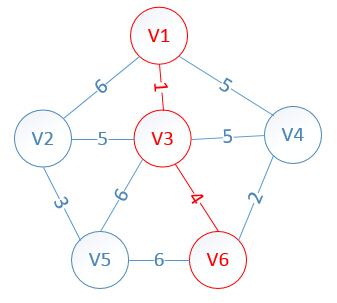
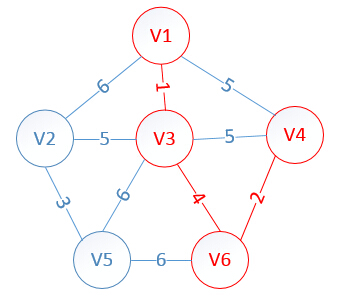
明显看出，以V6为终点的边的权值最小=4，所以边<mst[6],6>=4加入MST

 

此时，因为点V6的加入，需要更新lowcost数组和mst数组：

 

lowcost[2]=5，lowcost[3]=0，lowcost[4]=2，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=6，mst[5]=3，mst[6]=0

 

 

明显看出，以V4为终点的边的权值最小=2，所以边<mst[4],4>=4加入MST

 

此时，因为点V4的加入，需要更新lowcost数组和mst数组：

 

lowcost[2]=5，lowcost[3]=0，lowcost[4]=0，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=0，mst[5]=3，mst[6]=0

 

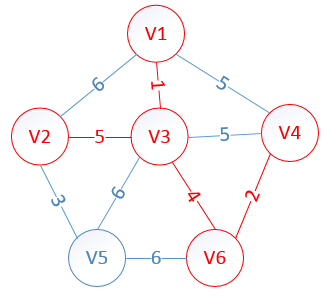
明显看出，以V2为终点的边的权值最小=5，所以边<mst[2],2>=5加入MST

 

此时，因为点V2的加入，需要更新lowcost数组和mst数组：

 

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=3，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=2，mst[6]=0

 

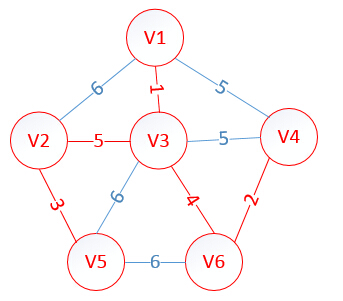
很明显，以V5为终点的边的权值最小=3，所以边<mst[5],5>=3加入MST

 

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=0，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=0，mst[6]=0

 

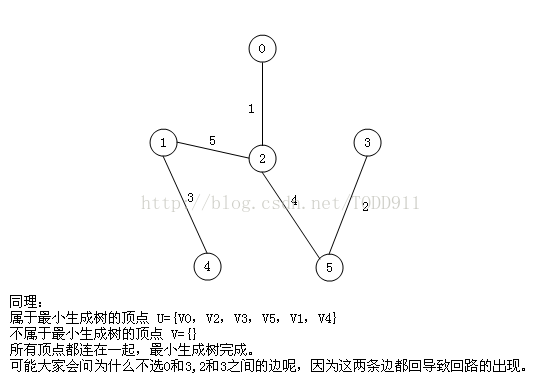
至此，MST构建成功，如图所示：

根据上面的过程，可以容易的写出具体实现代码如下（cpp）：

#include <stdio.h>
#include <stdlib.h>
 
#define MAX 100
#define MAXCOST 0x7fffffff

/*
测试数据如下：
7 11
A B 7
A D 5
B C 8
B D 9
B E 7
C E 5
D E 15
D F 6
E F 8
E G 9
F G 11

输出
A - D : 5
D - F : 6
A - B : 7
B - E : 7
E - C : 5
E - G : 9
Total:39

*/
 
int graph[MAX][MAX];
 
int Prim(int graph[][MAX], int n)
{
    /* lowcost[i]记录以i为终点的边的最小权值，当lowcost[i]=0时表示终点i加入生成树 */
    int lowcost[MAX];
 
    /* mst[i]记录对应lowcost[i]的起点，当mst[i]=0时表示起点i加入生成树 */
    int mst[MAX];
 
    int i, j, min, minid, sum = 0;
 
    /* 默认选择1号节点加入生成树，从2号节点开始初始化 */
    for (i = 2; i <= n; i++)
    {
        /* 最短距离初始化为其他节点到1号节点的距离 */
        lowcost[i] = graph[1][i];
 
        /* 标记所有节点的起点皆为默认的1号节点 */
        mst[i] = 1;
    }
 
    /* 标记1号节点加入生成树 */
    mst[1] = 0;
 
    /* n个节点至少需要n-1条边构成最小生成树 */
    for (i = 2; i <= n; i++)
    {
        min = MAXCOST;
        minid = 0;
 
        /* 找满足条件的最小权值边的节点minid */
        for (j = 2; j <= n; j++)
        {
            /* 边权值较小且不在生成树中 */
            if (lowcost[j] < min && lowcost[j] != 0)
            {
                min = lowcost[j];
                minid = j;
            }
        }
        /* 输出生成树边的信息:起点，终点，权值 */
        printf("%c - %c : %d/n", mst[minid] + 'A' - 1, minid + 'A' - 1, min);
 
        /* 累加权值 */
        sum += min;
 
        /* 标记节点minid加入生成树 */
        lowcost[minid] = 0;
 
        /* 更新当前节点minid到其他节点的权值 */
        for (j = 2; j <= n; j++)
        {
            /* 发现更小的权值 */
            if (graph[minid][j] < lowcost[j])
            {
                /* 更新权值信息 */
                lowcost[j] = graph[minid][j];
 
                /* 更新最小权值边的起点 */
                mst[j] = minid;//如果不用打出路径的话这个数组是不需要的
            }
        }
    }
    /* 返回最小权值和 */
    return sum;
}
 
int main()
{
    int i, j, k, m, n;
    int x, y, cost;
    char chx, chy;
 
    /* 读取节点和边的数目 */
    scanf("%d%d", &m, &n);
    getchar();
 
    /* 初始化图，所有节点间距离为无穷大 */
    for (i = 1; i <= m; i++)
    {
        for (j = 1; j <= m; j++)
        {
            graph[i][j] = MAXCOST;
        }
    }
 
    /* 读取边信息 */
    for (k = 0; k < n; k++)
    {
        scanf("%c %c %d", &chx, &chy, &cost);
        getchar();
        i = chx - 'A' + 1;
        j = chy - 'A' + 1;
        graph[i][j] = cost;
        graph[j][i] = cost;
    }
 
    /* 求解最小生成树 */
    cost = Prim(graph, m);
 
    /* 输出最小权值和 */
    printf("Total:%d/n", cost);
 
    return 0;    
}

kruskal（克鲁斯卡尔）算法

定义：

求加权连通图的最小生成树的算法。kruskal算法总共选择n- 1条边，所使用的贪婪准则是：从剩下的边中选择一条不会产生环路的具有最小耗费的边加入已选择的边的集合中。注意到所选取的边若产生环路则不可能形成一棵生成树。kruskal算法分e 步，其中e 是网络中边的数目。按耗费递增的顺序来考虑这e 条边，每次考虑一条边。当考虑某条边时，若将其加入到已选边的集合中会出现环路，则将其抛弃，否则，将它选入。

 

算法思想：

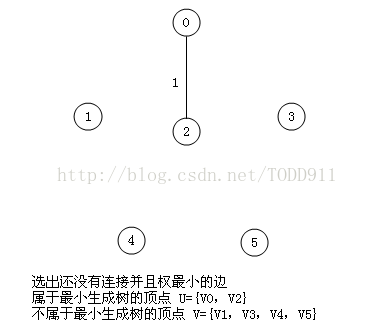
将每条边按照权值从小到大排序，每次取最小的权值边，如果加上该条边会产生环的话则放弃这条边，继续往下找小的，直到找出n-1条边为止，这个可以利用并查集来实现。

 

算法演示：

 

将上面poj那题再用kruskal算法做一遍

#include <iostream>  
#include <cstdio>  
#include <cmath>  
#include <cstring>  
#include <algorithm>  
using namespace std;  
const int N = 1001;  
const int E = 1000000;  
int n, M;  
int cent;  
int a[N];  
int Count = 0;  
   
typedef struct  
{  
    int x;  
    int y;  
    double vaule;  
}dian;  
dian m[E];  
   
typedef struct  
{  
    double x, y;  
}situation;  
situation p[N];  
   
double dis(situation a, situation b)  
{  
    return sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y) * (a.y - b.y));  
}  
   
bool cmp(dian a, dian b)  
{  
    return a.vaule < b.vaule;  
}  
   
void init()  
{  
    //                   cent 这里应该初始化到n  
    for (int i = 1; i <= n; i++)  
    {  
        a[i] = i;  
    }  
}  
   
int Find(int x)  
{  
    while (x != a[x])  
    {  
        x = a[x];  
    }  
    return x;  
}  
   
void Union(int x, int y)  
{  
    // 建议做路径压缩  
    int fx = Find(x);  
    int fy = Find(y);  
    if (fx != fy)  
    {  
        a[fx] = fy;  
    }  
}  
//kruskal模板   
double Kruskal()  
{  
    // init(); 不应该在这里init  
    sort(m, m + cent, cmp);  
    double result = 0;  
    for (int i = 0; i < cent&&Count != n - 1; i++)  
    {  
        if (Find(m[i].x) != Find(m[i].y))  
        {  
            Union(m[i].x, m[i].y);  
            result += m[i].vaule;  
            Count++;  
        }  
    }  
    return result;  
}  
   
int main()  
{  
    while (cin >> n >> M)  
    {  
         
        for (int i = 1; i <= n; i++)  
        {  
            cin >> p[i].x >> p[i].y;  
        }  
        cent = 0;  
        Count = 0;  
        for (int i = 1; i <= n; i++)  
        {  
            for (int j = i + 1; j <= n; j++)  
            {  
                m[cent].x = i;  
                m[cent].y = j;  
                m[cent++].vaule = dis(p[i], p[j]);  
            }  
        }  
        // init不应该放在Kruskal里面  
        init();  
        for (int i = 1; i <= M; i++)  
        {  
            int a, b;  
            cin >> a >> b;  
            // 这里还是要检查Find a 和 Find b是不是一样，不然Count会错  
            if (Find(a) != Find(b)) {  
                Union(a, b);  
                Count++;  
            }  
        }  
   
        printf("%.2f\n", Kruskal());  
    }  
    return 0;  
}