计算几何入门
前言
前置知识:初中数学,数学必修一,必修二部分内容,三角函数。
文中提到的矩阵啥的不用管,没什么用
向量
向量是一个有大小和方向的量,可以用有箭头的线段表示。若向量的起点为 \(A\),终点为 \(B\),则这个向量可以表示为 \(\overrightarrow {AB}\),或者 \(\vec a\)。
二位平面中充斥着无数的向量,通常为了方便表述一个向量,会将向量平移使得起点为原点,终点为 \(A(x,y)\),即一个点 \(A\) 表示向量 \(\overrightarrow {OA}\),可记为 \(\begin{bmatrix}x\\y\end{bmatrix}\)。
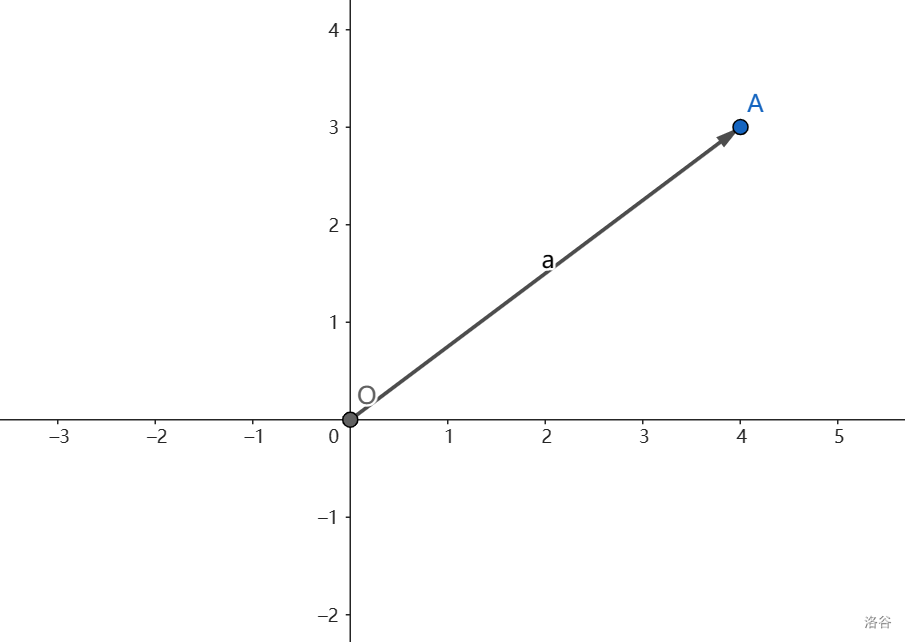
向量的模
向量的模长,即长度。向量 \(\vec a\) 的模长记为 \(|\vec a|\),即 \(\sqrt{x^2+y^2}\)。
相反向量
方向相反,大小相等的向量为相反向量。向量 \(\vec a\) 的相反向量记为为 \(-\vec a\)。
垂直向量
若向量 \(\vec a\) 和 \(\vec b\) 所在的直线相互垂直,则 \(\vec a\) 和 \(\vec b\) 互为垂直向量。
共线向量
若向量 \(\vec a\) 和 \(\vec b\) 所在的直线平行,则 \(\vec a\) 和 \(\vec b\) 互为共线向量。
零向量
零向量的模长为 \(0\),方向任意,它与任何一个向量都共线,坐标为 \((0,0)\)。
向量的加法
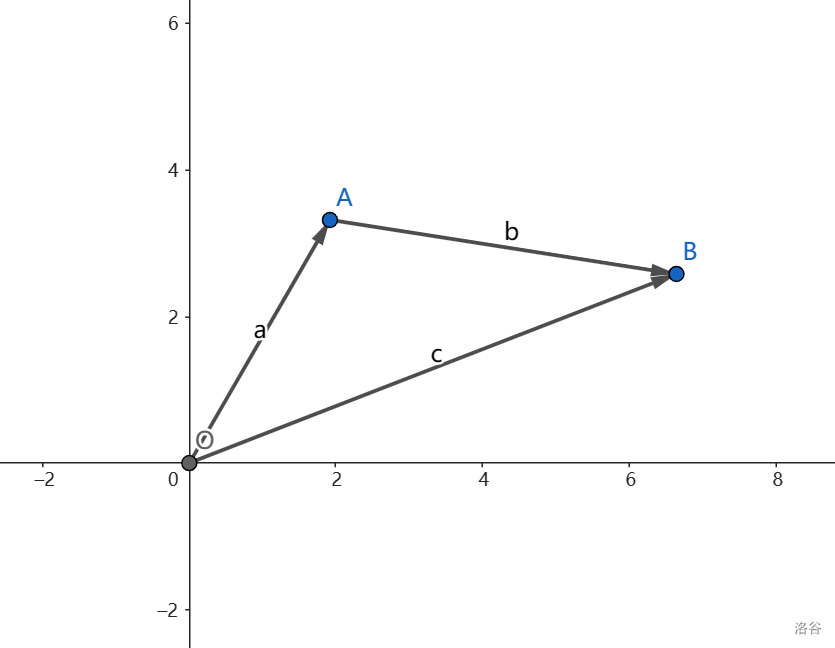
若将向量看成一种移动的话,那么如上图。先按 \(\vec a\) 从 \(O\) 走到 \(A\) 点,再按照 \(\vec b\) 走到 \(B\) 点是相当于之间从 \(O\) 点走向 \(B\) 点的,即 \(\vec c=\vec a+\vec b\)。若记 \(\vec a=\begin{bmatrix}x_1\\y_1\end{bmatrix},\vec b=\begin{bmatrix}x_2\\y_2\end{bmatrix}\),矩阵上的意义为
向量的减法
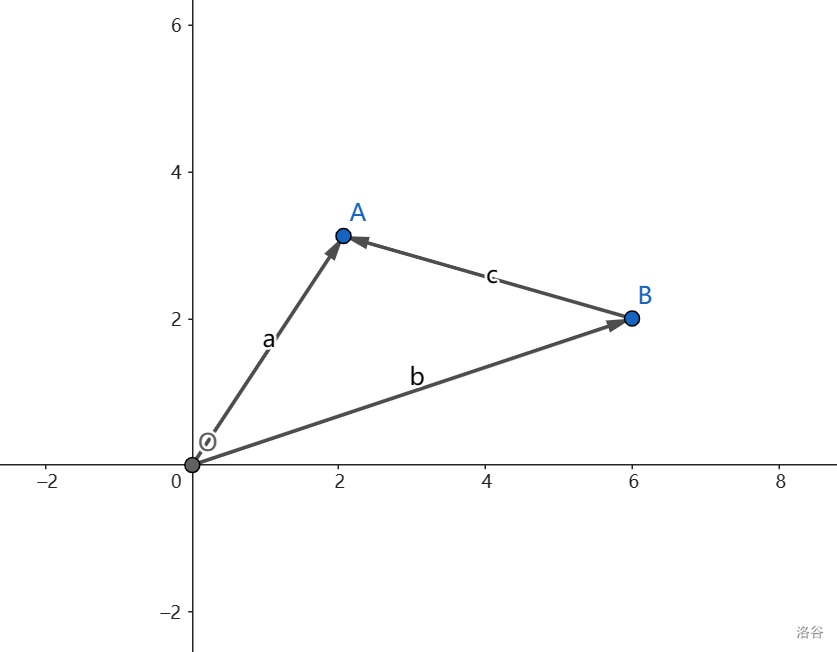
可以将 \(\vec a-\vec b\) 看成 \(\vec a+(-\vec b)\),那么就可以用到加法了。记 \(\vec c=\vec a-\vec b\),则 \(\vec c\) 的起点为 \(\vec b\) 的终点,\(\vec c\) 的终点为 \(\vec a\) 的终点,通常可以方便获得两个点之间的向量。例如上图中 \(\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}\)。
向量的数乘
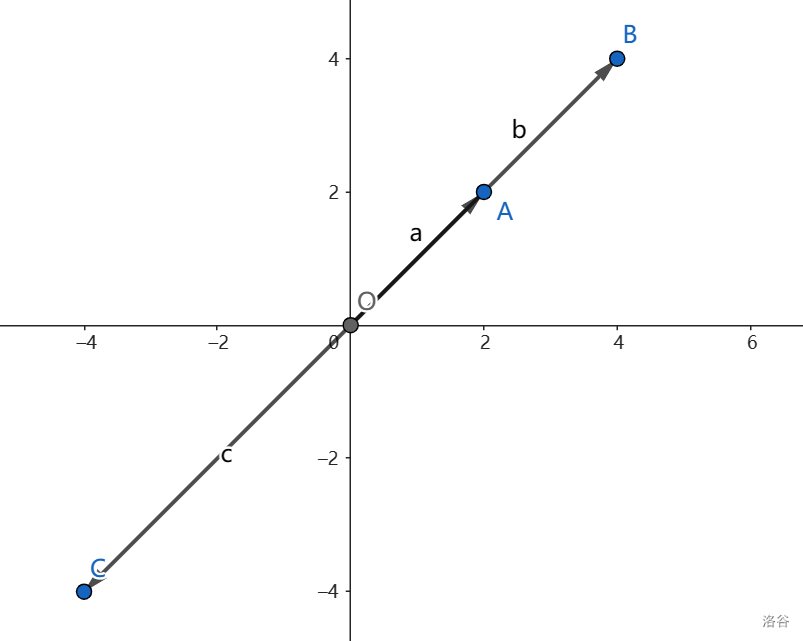
向量的数乘可记作 \(\vec b=\lambda\vec a\)。\(\vec a\) 和 \(\vec b\) 的模长之间的关系为 \(|\vec b|=|\lambda||\vec a|\)。若 \(\lambda>0\),则 \(\vec b\) 的方向与 \(\vec a\) 相同;若 \(\lambda=0\),则 \(\vec b\) 为零向量;若 \(\lambda<0\),则 \(\vec b\) 的方向与 \(\vec a\) 相反。
若 \(\vec a=\begin{bmatrix}x\\y\end{bmatrix}\),则矩阵上的意义可看作为
向量的点积
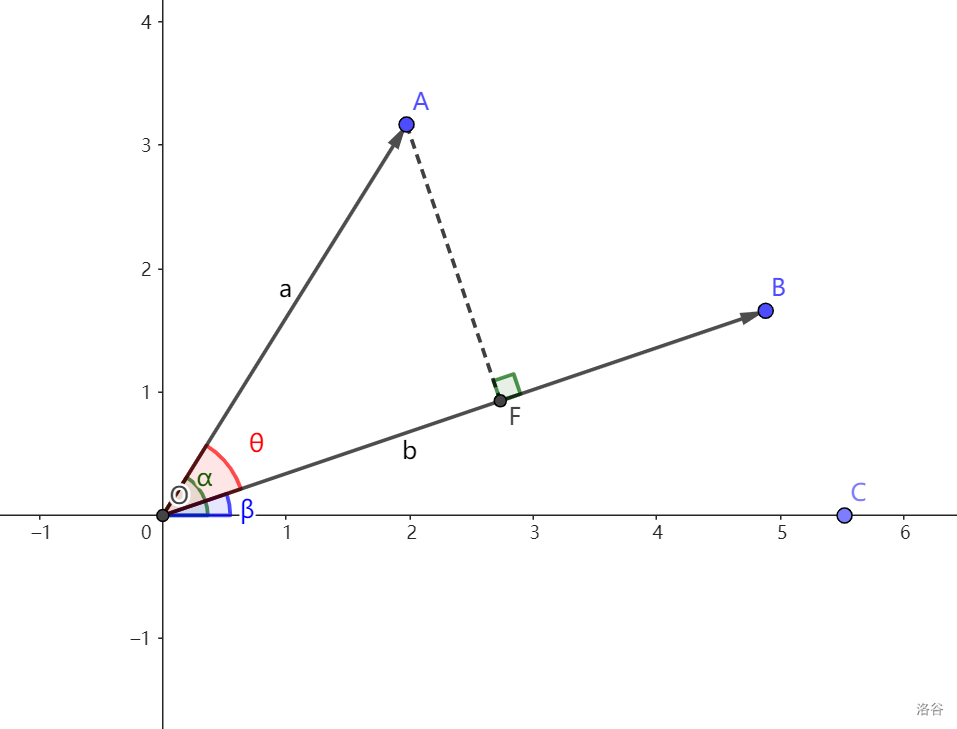
点积,又名数量积,点乘,点积的几何意义为 \(\vec a\) 的在 \(\vec b\) 所在直线的投影的长度与 \(|\vec b|\) 的乘积。记作 \(\vec a\cdot\vec b\)。通常可以省略中间的点乘。如上图,这里 \(\vec a\cdot\vec b=|\vec a||\vec b|\cdot\cos \left\langle\vec a,\vec b\right\rangle =OF\cdot OB\)。这里还是记作 \(\vec a\) 的坐标为 \((x_1,y_1)\),\(\vec b\) 的坐标为 \((x_2,y_2)\)。下面给个结论:\(\vec a\cdot\vec b=x_1x_2+y_1y_2\)。
证明:
以上图为例,若 \(x\) 正半轴上有一点 \(C\),记 \(\angle AOB=\theta,\angle AOC=\alpha,\angle BOC=\beta\)。
有 \(\cos\alpha=\dfrac{x_1}{|\vec a|},\cos\beta=\dfrac{x_2}{|\vec b|},\sin\alpha=\dfrac{y_1}{|\vec a|},\sin\beta=\dfrac{y_2}{|\vec b|}\)。
根据三角恒等变换有 \(\cos\theta=\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)。
分别将 \(\cos\alpha,\cos\beta,\sin\alpha,\sin\beta\) 代入,得
得到 \(|\vec a||\vec b|\cdot\cos \left\langle\vec a,\vec b\right\rangle=x_1x_2+y_1y_2\),命题得证。
显然点积是有交换律的,因为 \(\cos\alpha=\cos(-\alpha)\)。
点积可用于判断向量之间的前后关系。
-
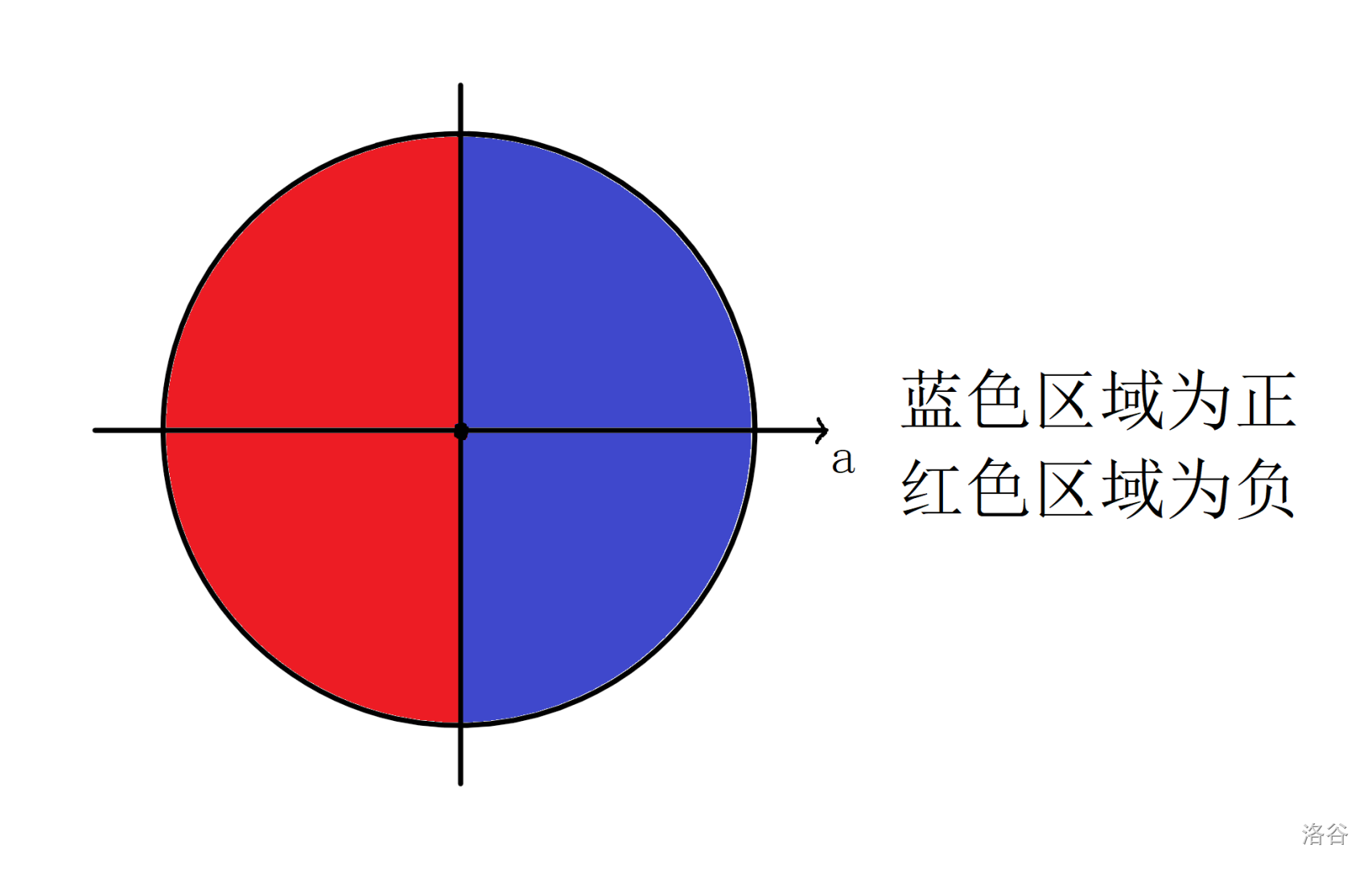
若两个向量共线且同向,那么它们的点积为他们的模长之积。
-
若 \(\left\langle\vec a,\vec b\right\rangle<\dfrac{\pi}{2}\),则 \(\vec a\cdot\vec b>0\)。
-
若 \(\left\langle\vec a,\vec b\right\rangle=\dfrac{\pi}{2}\),则 \(\vec a\cdot\vec b=0\)。
-
若 \(\left\langle\vec a,\vec b\right\rangle>\dfrac{\pi}{2}\),则 \(\vec a\cdot\vec b<0\)。
-
若两个向量共线且反向,那么它们的点积为他们的模长之积的相反数。
如下图,直观的反应了夹角与点积的关系。
向量的叉积
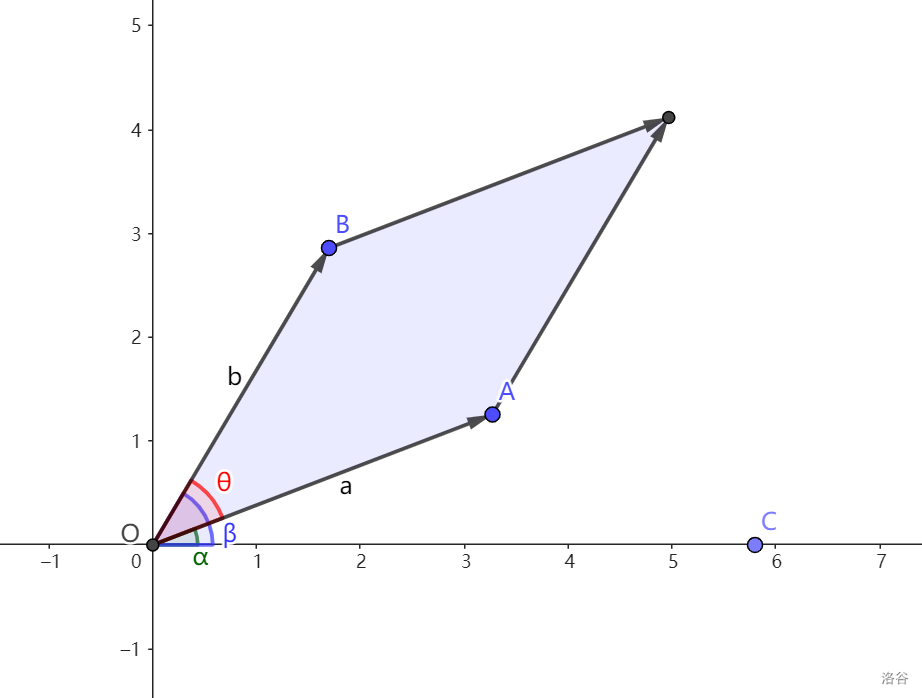
又称外积,几何意义为向量根据平行四边形法则围成的面积。记为 \(\vec a\times\vec b\)。根据几何意义,显然有 \(\vec a\times\vec b=|a||b|\sin\left\langle\vec a,\vec b\right\rangle\)。记作 \(\vec a\) 的坐标为 \((x_1,y_1)\),\(\vec b\) 的坐标为 \((x_2,y_2)\)。这里同样给个结论:\(\vec a\times\vec b=x_1y_2-x_2y_1\)。
证明:
仿照点积的证明,我们同样在 \(x\) 正半轴上取一点 \(C\),记 \(\angle AOB=\theta,\angle AOC=\alpha,\angle BOC=\beta\)。
有 \(\sin\beta=\dfrac{y_2}{|\vec b|},\cos\alpha=\dfrac{x_1}{|\vec a|},\cos\beta=\dfrac{x_2}{|\vec b|},\sin\alpha=\dfrac{y_1}{|\vec a|}\)。
根据三角恒等变换有 \(\sin\theta=\sin(\beta-\alpha)=\sin\beta\cos\alpha-\cos\beta\sin\alpha\)。
分别将 \(\sin\beta,\cos\alpha,\cos\beta,\sin\alpha\) 代入,得
得到 \(|\vec a||\vec b|\cdot\sin \left\langle\vec a,\vec b\right\rangle=x_1y_2-x_2y_1\),命题得证。
另一种更为直观的证明:
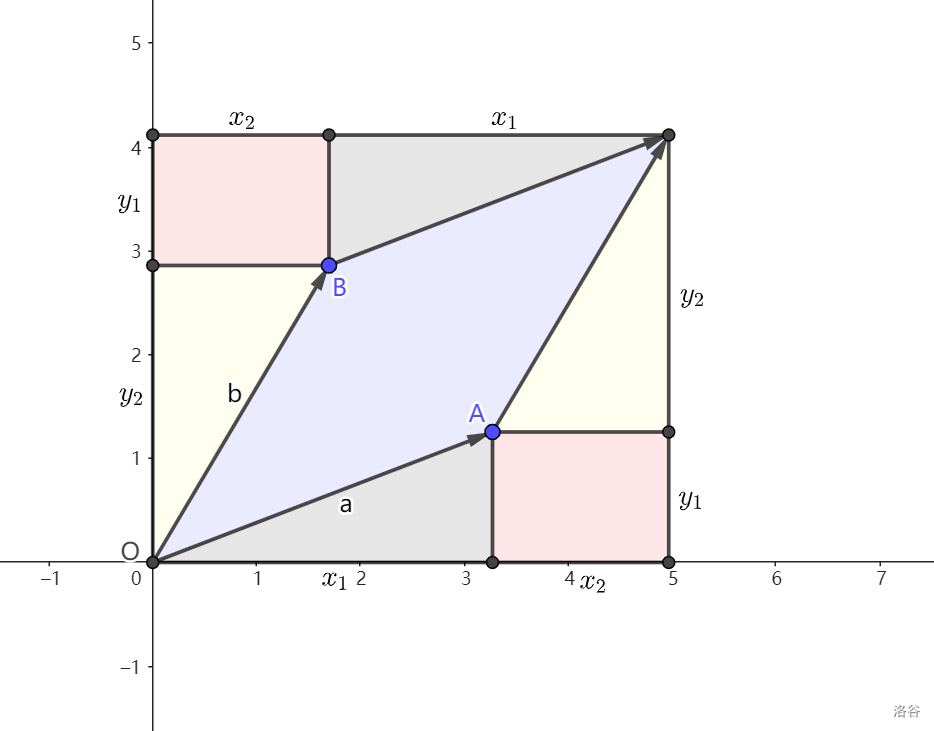
如上图,我们可以用用割补法将蓝色部分的面积求出。颜色相同的面积是相等的,这个用全等不难证出,那么 \(\vec a\times\vec b=(x_1+x_2)(y_1+y_2)-x_1y_1-x_2y_2-2x_2y_1=x_1y_2-x_2y_1\)。
叉积是没有交换律的,因为 \(\sin\alpha\ne\sin(-\alpha)\)。
向量与矩阵之间有着密切的联系,叉积运算可看作是
叉积可用于判断向量之间的左右关系。
-
若两个向量共线,则 \(\vec a\times\vec b=0\)。
-
若 \(\vec b\) 的终点在 \(\vec a\) 的左侧,则 \(\vec a\times\vec b>0\)。
-
若 \(\vec b\) 的终点在 \(\vec a\) 的右侧,则 \(\vec a\times\vec b<0\)。
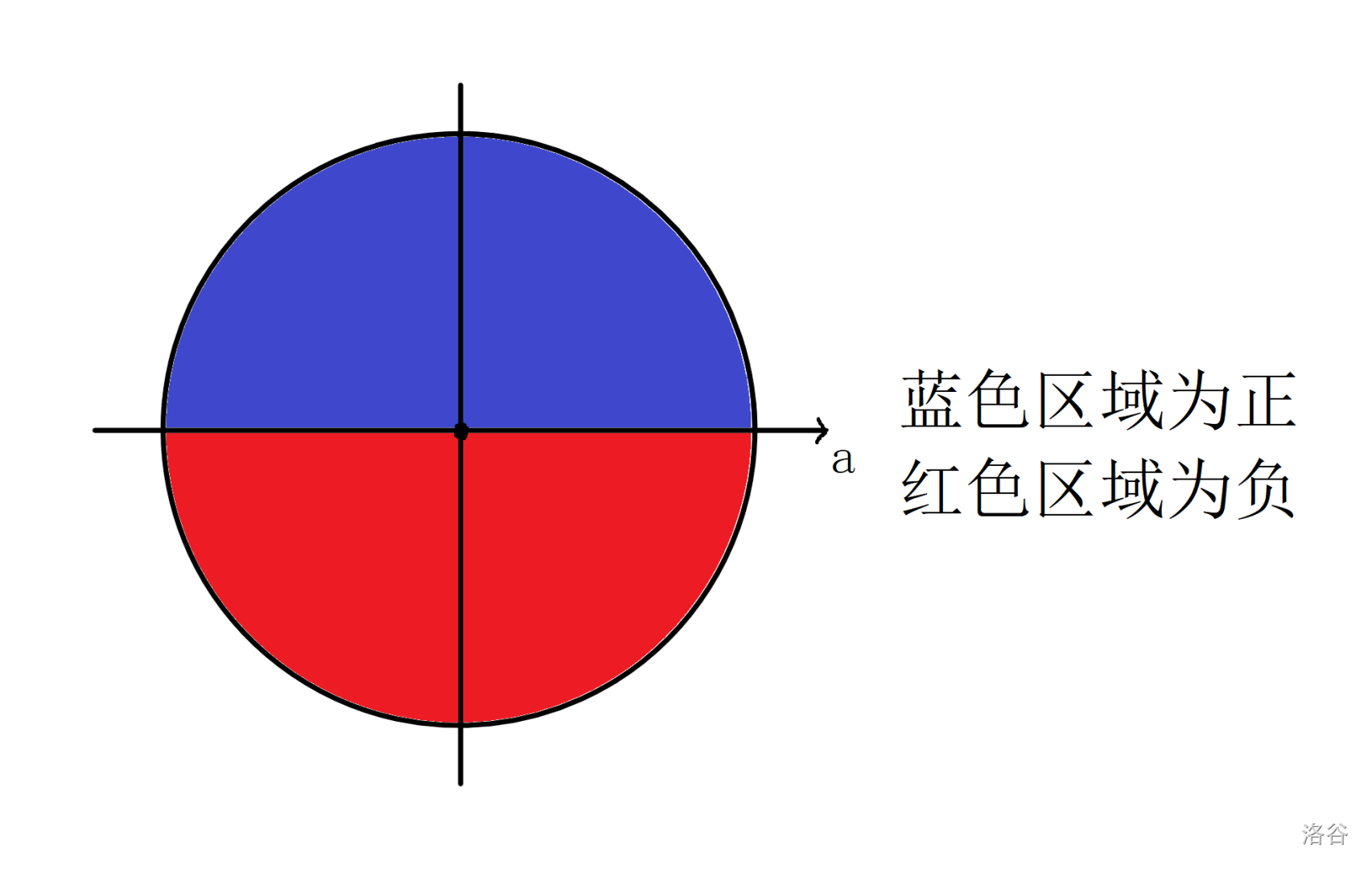
讲了这么多,向量的代码先放一下。
const double eps = 1e-8;//根据题目自选,通常这个好
int sgn(double x) { return fabs(x) < eps ? 0 : x > 0 ? 1 : -1; }//用于判断符号的
struct point {//向量,也可表示点
double x, y;
point(double x = 0, double y = 0) : x(x), y(y) {}
point operator + (const point &b) const { return point(x+b.x, y+b.y); }//加法
point operator - (const point &b) const { return point(x-b.x, y-b.y); }//减法
point operator * (const double &k) const { return point(x*k, y*k); }//数乘,乘法
point operator / (const double &k) const { return point(x/k, y/k); }//数乘,除法
};
double dot(point a, point b) { return a.x*b.x+a.y*b.y; }//点积
double crs(point a, point b) { return a.x*b.y-b.x*a.y; }//差积
double len(point a) { return sqrt(a.x*a.x+a.y*a.y); }//模长
线段交点
根据叉积我们可以求出线段的交点。
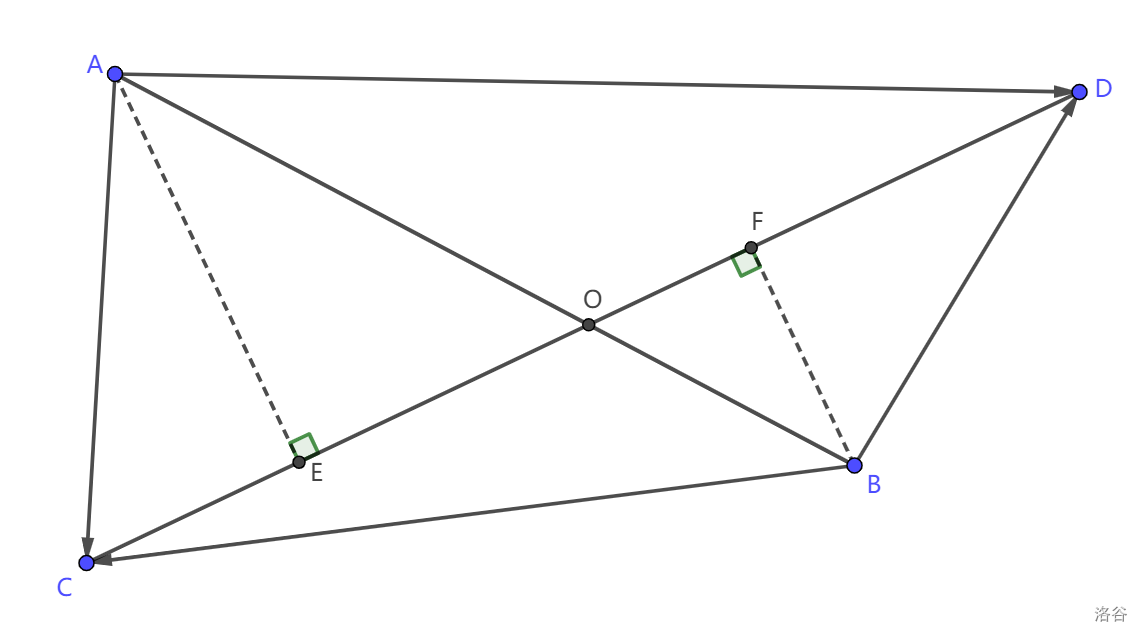
如上图,\(AB\) 交 \(CD\) 与点 \(O\),\(A,B,C,D\) 的坐标已知,求点 \(O\) 的坐标。
先作 \(AE\bot CD\) 交于点 \(E\),\(BF\bot CD\) 交于点 \(F\)。
有 \(S_{\triangle CAD}=\dfrac{\overrightarrow{AC}\times\overrightarrow{AD}}{2},S_{\triangle CBD}=\dfrac{\overrightarrow{BD}\times\overrightarrow{BC}}{2}\)
因为 \(\triangle CAD\) 和 \(\triangle CBD\) 共用 \(CD\) 这条底边。
所以 \(\dfrac{AE}{BF}=\dfrac{\overrightarrow{AC}\times\overrightarrow{AD}}{\overrightarrow{BD}\times\overrightarrow{BC}}\)。
显然有 \(\triangle AOE\backsim\triangle BOF\)。
所以 \(\dfrac{AO}{BO}=\dfrac{AE}{BF}=\dfrac{\overrightarrow{AC}\times\overrightarrow{AD}}{\overrightarrow{BD}\times\overrightarrow{BC}}\)。
所以 \(\overrightarrow{AO}=\overrightarrow{AB}\times\dfrac{\overrightarrow{AC}\times\overrightarrow{AD}}{\overrightarrow{AC}\times\overrightarrow{AD}+\overrightarrow{BD}\times\overrightarrow{BC}}\)。
即可求出 \(O\)。
特别地,若 \(AB\) 与 \(CD\) 没有交点,上述求的即为 \(AB\) 所在的直线与 \(CD\) 所在的直线的交点。也就是说,其实 \(AB\) 和 \(CD\) 是否有交点我们是不关心的,读者可以自己画几个图推一推。
代码:
struct line {
point s, e; double ang;//ang为线段与x轴的夹角
line() {}
line(point a, point b) { s = a, e = b, ang = atan2((b-a).y, (b-a).x); }
bool operator < (const line &b) const { return sgn(ang-b.ang) ? ang < b.ang : sgn(crs(b.s-s, b.e-s)) > 0; }//极角排序
};
point get(line a, line b) { double x = crs(b.s-a.s, b.e-a.s), y = crs(b.e-a.e, b.s-a.e); return a.s+(a.e-a.s)*x/(x+y); }//求线段的交点
向量旋转
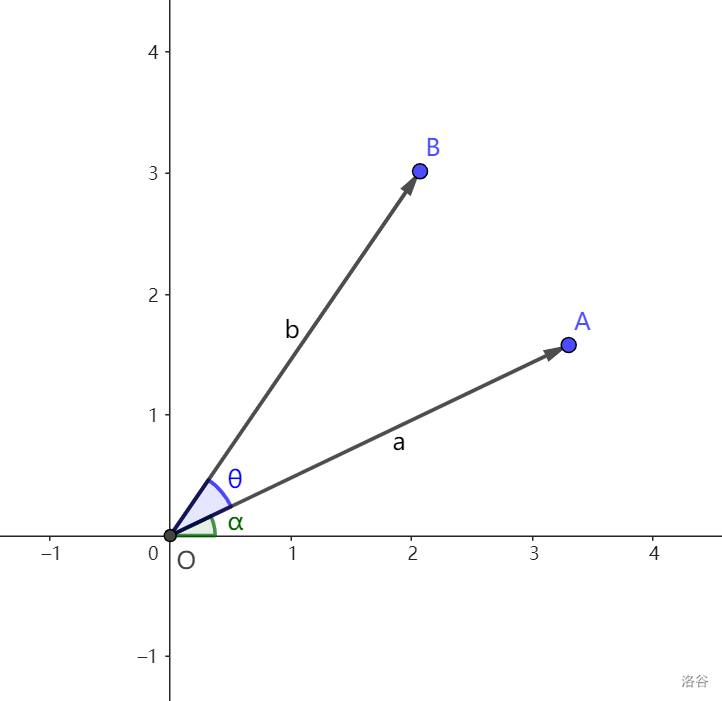
如图,有一向量 \(\vec a\) 绕点 \(O\) 逆时针旋转 \(\theta\) 度到向量 \(\vec b\),如何表示出 \(\vec b\) 的坐标?
记 \(\vec a\) 的坐标为 \((x,y)\),\(l=\sqrt{x^2+y^2}\),那么有 \(x=l\cos\alpha,y=l\sin\alpha\)。
\(B\) 的坐标为 \((l\cos(\alpha+\theta),l\sin(\alpha+\theta))\)。
根据三角恒等变换,有 \(\cos(\alpha+\theta)=\cos\alpha\cos\theta-\sin\alpha\sin\theta,\sin(\alpha+\theta))=\sin\alpha\cos\theta+\cos\alpha\sin\theta\)。
将 \(x,y\) 带入进去,那么得 \(B\) 的坐标为 \((x\cos\theta-y\sin\theta,y\cos\theta+x\sin\theta)\)。
代码:
point rotate(point a, double x) { return point(a.x*cos(x)-a.y*sin(x), a.y*cos(x)+a.x*sin(x)); }
三角剖分求面积
向量的叉积所求的面积是有向的,方向用正负表示。若给一个多边形,只要逆时针的把相邻两个点的叉积一次累加起来,就能得到这个多边形的面积,这是一个类似容斥的过程,下面举个例子,方便读者更好的体会这个过程。
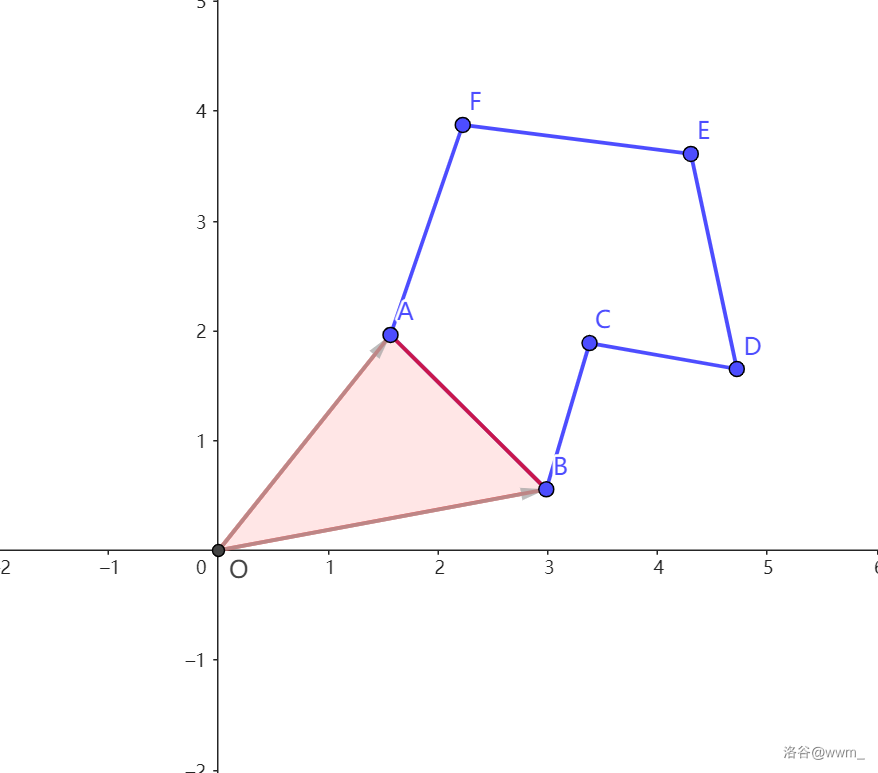
对于多边形 \(ABCDEF\),我们先求 \(\overrightarrow{OA}\times\overrightarrow{OB}\) 的值,得到图中红色的面积(红色为负的,蓝色为正的)。
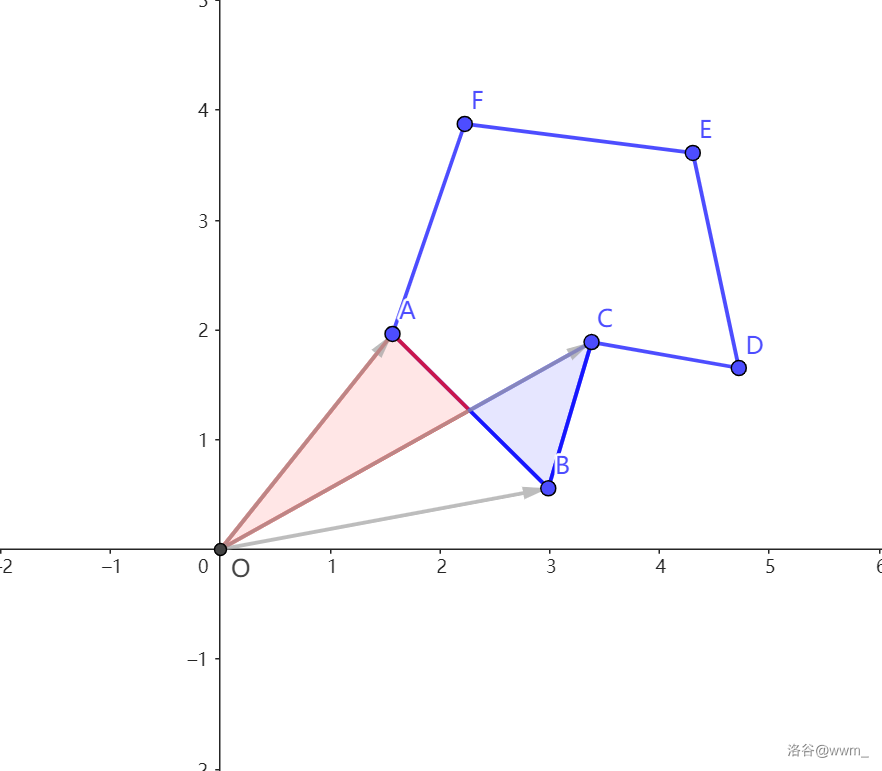
接下来算 \(B,C\) 的。
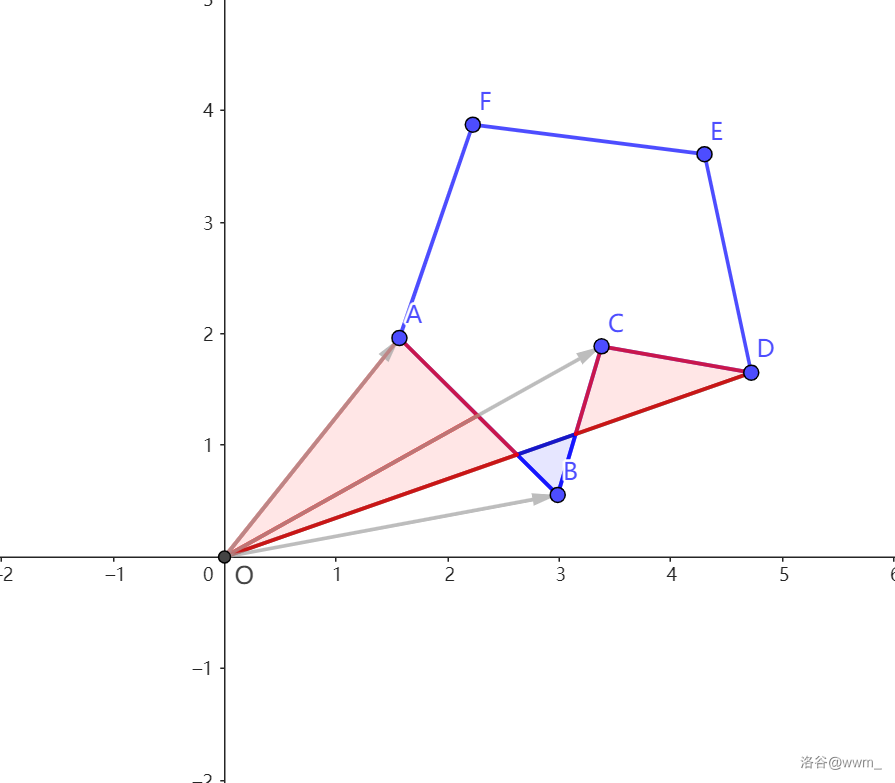
接下来算 \(C,D\) 的。
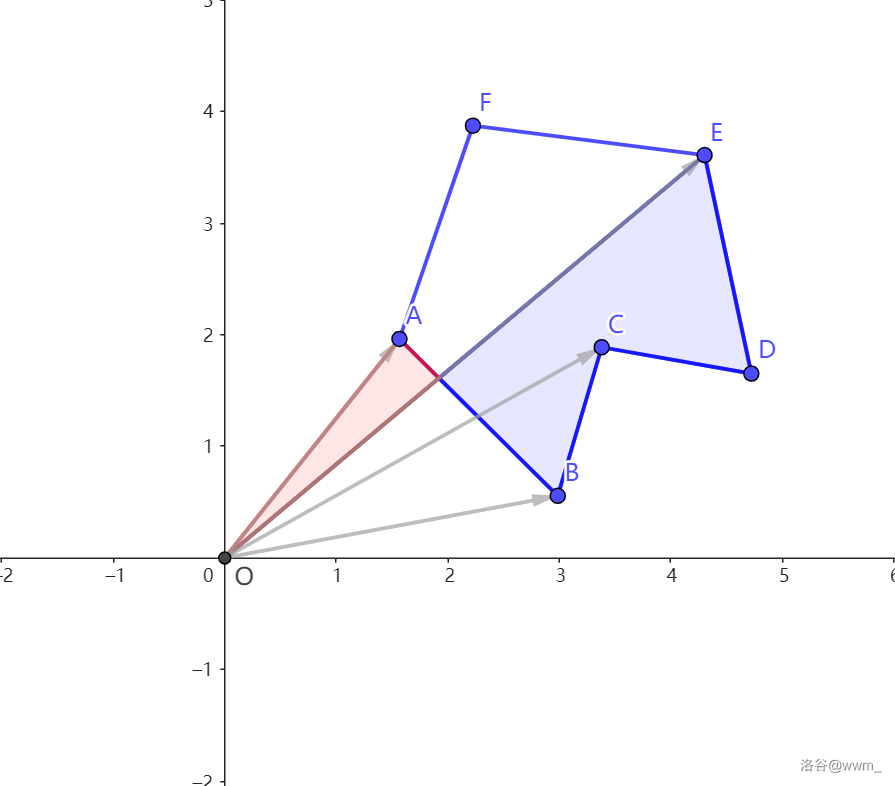
接下来算 \(D,E\) 的。
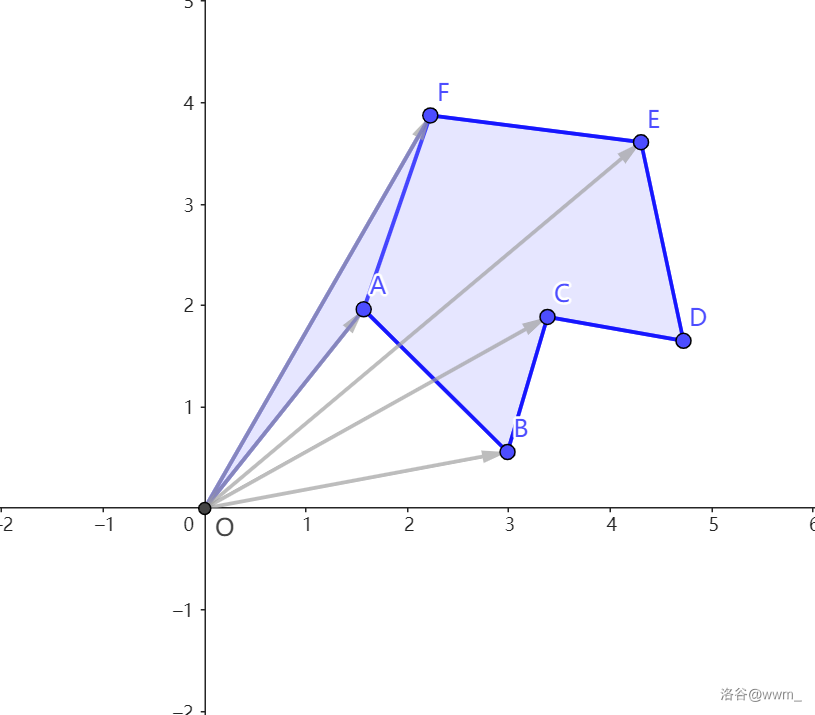
接下来算 \(E,F\) 的。
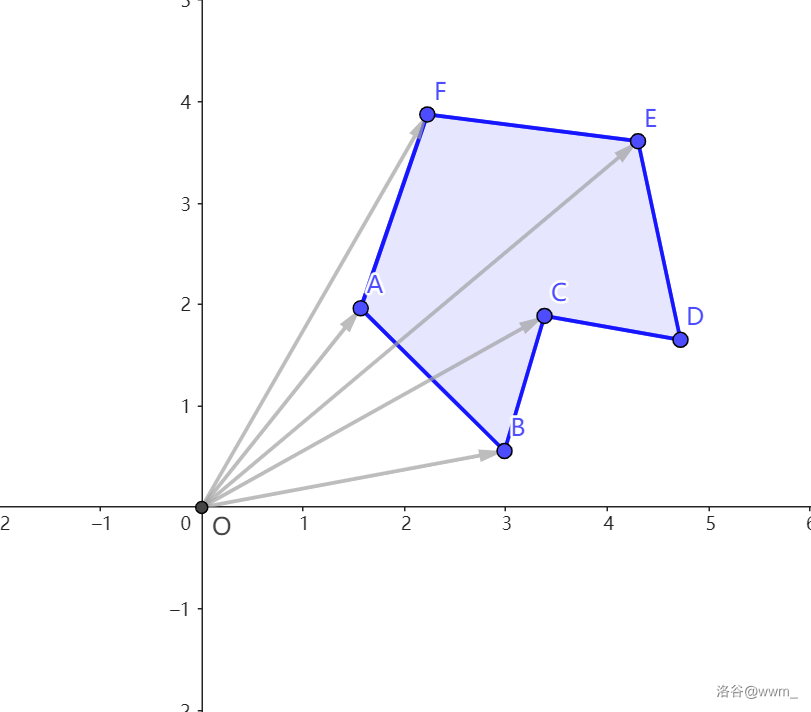
最后算 \(F,A\) 的,算法结束,累加的面积即为多边形的面积。
代码:
...//逆时针输入一个n个点的多边形
for (int i = 1; i <= n; ++i) ans += crs(p[i], p[i == n ? 1 : i+1]);
printf("%.2lf", fabs(ans)/2);
凸包
想象一个平面有 \(n\) 个点,若用一条绳子将这 \(n\) 个点包起来,求出绳子的最小长度。
首先这条绳子所围成的多边形一定为凸多边形,否则根据三角形不等式得出一定不是最优的,可以直接连边,如下图所示:
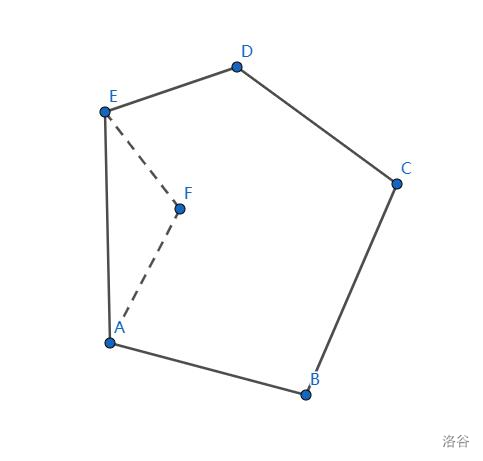
那么下面介绍两个算法:
Graham 算法
第一步我们需要找到一个纵坐标最小的点(如有相同的取横坐标最小的),然后极角排序,接下来从第一个点开始扫描每个点。过程中需要维护一个栈,也是当前我们凸包已经选的点,若当前点与栈顶的点的连线与上一条方向不符时,那么去掉栈顶的点,直到符合要求时加入栈。扫描完毕时栈中的点集即为凸包的点。
下面是图解:
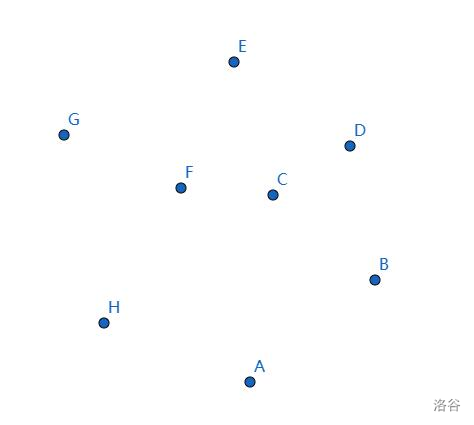
若干点。
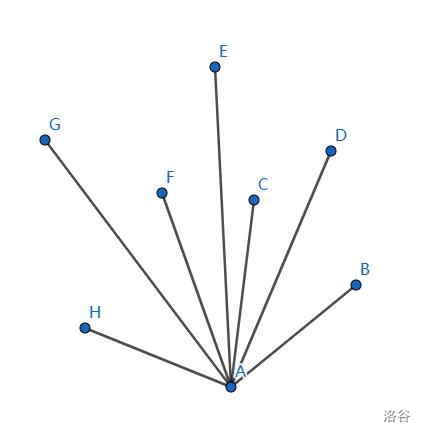
选出 \(A\) 点,极角排序。
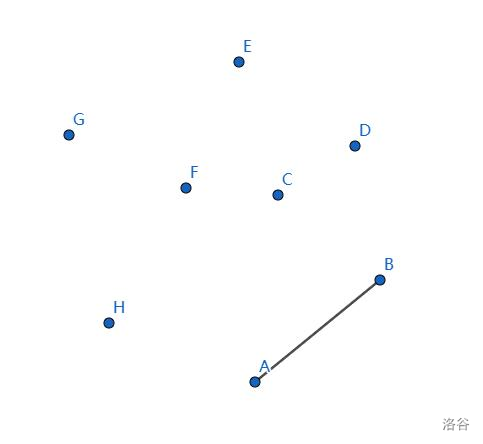
栈中加入 \(B\) 点,没什么问题。
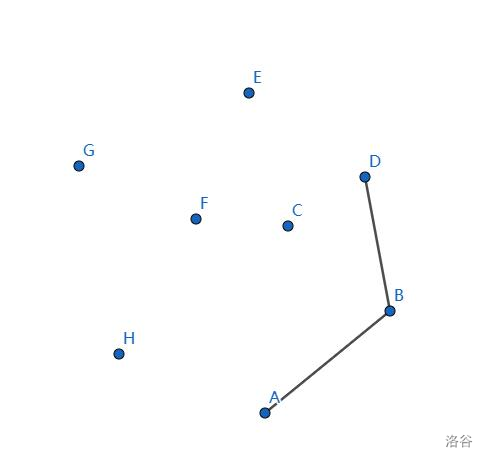
栈中加入 \(D\) 点,没什么问题。
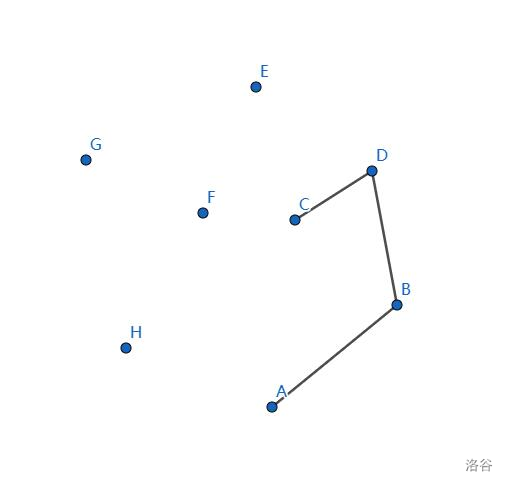
栈中加入 \(C\) 点,没什么问题。
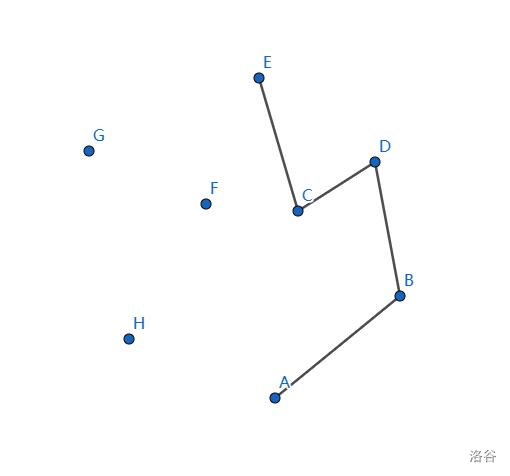
栈中加入 \(E\) 点,不呈凸多边形,栈中排出 \(C\)。
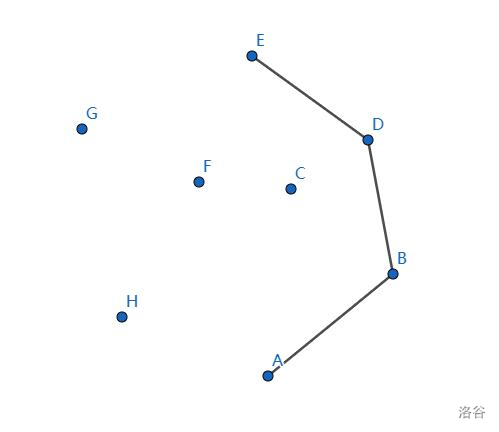
符合要求。
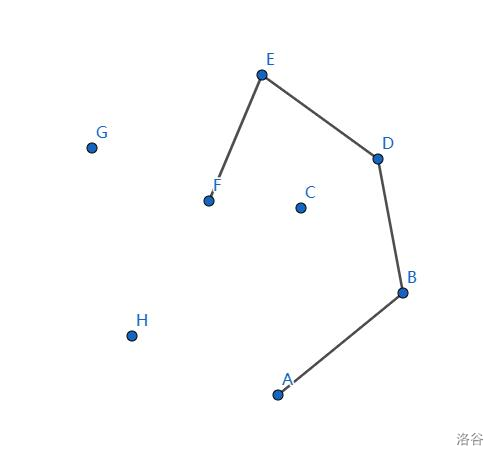
栈中加入 \(F\) 点,没什么问题。
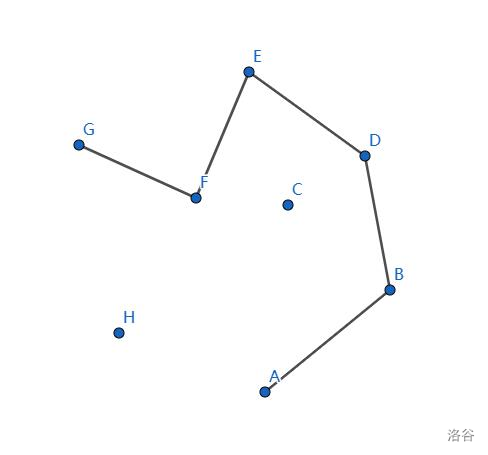
栈中加入 \(G\) 点,不呈凸多边形,栈中排出 \(F\)。
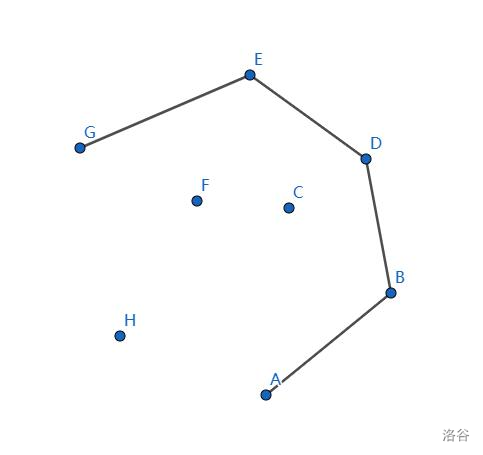
符合要求。
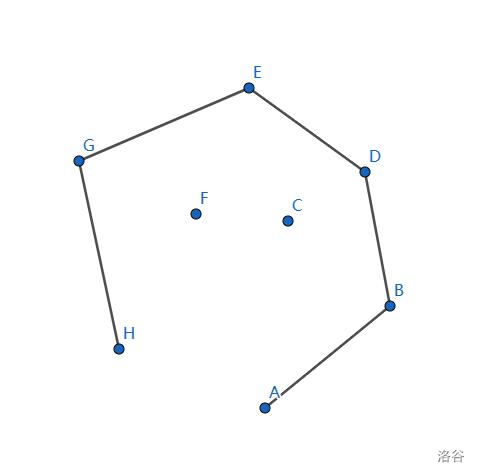
栈中加入 \(H\) 点,没什么问题。
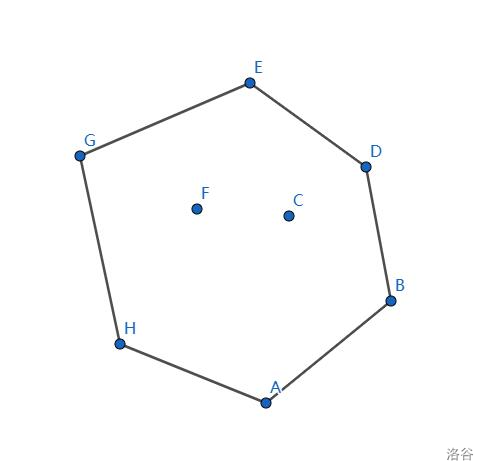
最后算法结束,栈中为 \(A,B,D,E,G,H\),为凸包的点(逆时针排列)。
代码:
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
typedef vector <int> vi;
typedef pair <int, int> pii;
inline int rd() { int x = 0, f = 1; char c = getchar(); while (!isdigit(c)) f = c == '-' ? -1 : f, c = getchar(); while (isdigit(c)) x = (x<<3)+(x<<1)+(c^48), c = getchar(); return x*f; }
inline ll rdll() { ll x = 0, f = 1; char c = getchar(); while (!isdigit(c)) f = c == '-' ? -1 : f, c = getchar(); while (isdigit(c)) x = (x<<3)+(x<<1)+(c^48), c = getchar(); return x*f; }
template <typename T> inline void write(T x) { if (x < 0) x = -x, putchar('-'); if (x > 9) write(x/10); putchar(x%10+48); }
const double eps = 1e-8;
const int N = 1e5+5;
struct point {
double x, y;
point(double x = 0, double y = 0) : x(x), y(y) {}
point operator + (const point &b) const { return point(x+b.x, y+b.y); }
point operator - (const point &b) const { return point(x-b.x, y-b.y); }
point operator * (const double &k) const { return point(x*k, y*k); }
point operator / (const double &k) const { return point(x/k, y/k); }
} p[N], s[N];
double dot(point a, point b) { return a.x*b.x+a.y*b.y; }
double crs(point a, point b) { return a.x*b.y-b.x*a.y; }
int sgn(double x) { return fabs(x) < eps ? 0 : x > 0 ? 1 : -1; }
double len(point a) { return sqrt(a.x*a.x+a.y*a.y); }
double dist(point a, point b) { return len(a-b); }
bool cmp(point x, point y) { return sgn(crs(x-p[1],y-p[1])) > 0 ? 1 : sgn(crs(x-p[1], y-p[1])) < 0 ? 0 : dist(p[1], x) < dist(p[1], y); }
int main() {
int n = rd(), top = 0;
for (int i = 1; i <= n; ++i) {
scanf("%lf%lf", &p[i].x, &p[i].y);
if (i > 1 && (p[i].y < p[1].y || (p[i].y == p[1].y && p[i].x < p[1].x))) swap(p[1], p[i]);
}
sort(p+2, p+n+1, cmp);
s[++top] = p[1];
for (int i = 2; i <= n; ++i) {
while (top > 1 && sgn(crs(s[top]-s[top-1], p[i]-s[top])) <= 0) --top;
s[++top] = p[i];
}
s[++top] = p[1];
double ans = 0;
for (int i = 1; i < top; ++i) ans += dist(s[i], s[i+1]);
printf("%.2lf", ans);
return 0;
}
还在施工中 qwq……


 浙公网安备 33010602011771号
浙公网安备 33010602011771号